
题目列表(包括答案和解析)
9.(磨中)a和b为异面直线,则过a与b垂直的平面( )
A、有且只有一个 B、一个面或无数个
C、可能不存在 D、可能有无数个
正确答案:C
错误原因:过a与b垂直的夹平面条件不清
8.(磨中)下列正方体或正四面体中,P、Q、R、S分别是所在棱的中点,这四个点不共面的一个图是( )
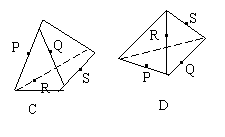
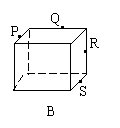
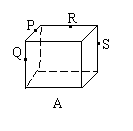
正确答案:D
错误原因:空间观点不强
7.(磨中)已知一个正四面体和一个正八面体的棱长相等,把它们拼接起来,使一个表面重合,所得多面体的面数有( )
A、7 B、8 C、9 D、10
正确答案:A
错误原因:4+8-2=10
6.(磨中)给出下列命题:①分别和两条异面直线AB、CD同时相交的两条直线AC、BD一定是异面直线②同时与两条异面直线垂直的两直线不一定平行③斜线b在面α内的射影为c,直线a⊥c,则a⊥b④有三个角为直角的四边形是矩形,其中真命题是( )
正确答案:①
错误原因:空间观念不明确,三垂线定理概念不清
5. (石庄中学)下列命题中:
① 若向量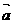 、
、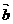 与空间任意向量不能构成基底,则
与空间任意向量不能构成基底,则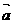 ∥
∥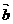 。
。
② 若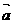 ∥
∥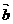 ,
, 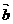 ∥
∥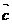 ,则
,则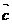 ∥
∥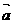 .
.
③ 若 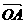 、
、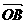 、
、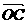 是空间一个基底,且
是空间一个基底,且 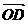 =
=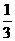
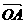 +
+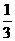
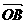 +
+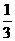
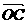 ,则A、B、C、D四点共面。
,则A、B、C、D四点共面。
④ 若向量 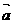 +
+ 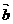 ,
, 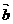 +
+ 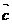 ,
, 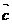 +
+ 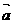 是空间一个基底,则
是空间一个基底,则 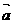 、
、 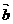 、
、 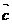 也是空间的一个基底。其中正确的命题有( )个。
也是空间的一个基底。其中正确的命题有( )个。
A 1 B 2 C 3 D 4
正确答案:C 错因:学生对空间向量的基本概念理解不够深刻。
4.(石庄中学)正方体ABCD-A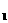 B
B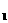 C
C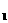 D
D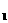 中,点P在侧面BCC
中,点P在侧面BCC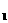 B
B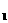 及其边界上运动,并且总保持AP⊥BD
及其边界上运动,并且总保持AP⊥BD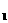 ,则动点P的轨迹( )
,则动点P的轨迹( )
A 线段B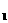 C
B BB
C
B BB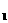 的中点与CC
的中点与CC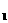 中点连成的线段
中点连成的线段
C 线段BC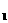 D CB中点与B
D CB中点与B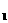 C
C 中点连成的线段
中点连成的线段
正确答案:A 错因:学生观察能力较差,对三垂线定理逆定理不能灵活应用。
3.(石庄中学)已知平面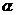 ∥平面
∥平面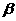 ,直线L
,直线L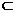 平面
平面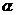 ,点P
,点P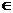 直线L,平面
直线L,平面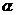 、
、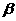 间的距离为8,则在
间的距离为8,则在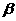 内到点P的距离为10,且到L的距离为9的点的轨迹是( )
内到点P的距离为10,且到L的距离为9的点的轨迹是( )
A 一个圆 B 四个点 C 两条直线 D 两个点
正确答案:B 错因:学生对点线距离、线线距离、面面距离的关系不能灵活掌握。
2.(石庄中学)在正方体ABCD-A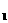 B
B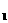 C
C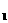 D
D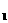 ,O是底面ABCD的中心,M、N分别是棱DD
,O是底面ABCD的中心,M、N分别是棱DD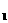 、D
、D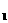 C
C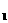 的中点,则直线OM( )
的中点,则直线OM( )
A 是AC和MN的公垂线 B 垂直于AC但不垂直于MN
C 垂直于MN,但不垂直于AC D 与AC、MN都不垂直
正确答案:A 错因:学生观察能力较差,找不出三垂线定理中的射影。
1.(石庄中学)设ABCD是空间四边形,E,F分别是AB,CD的中点,则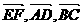 满足( )
满足( )
A 共线 B 共面 C 不共面 D 可作为空间基向量
正确答案:B 错因:学生把向量看为直线。
10. (如中)已知双曲线两焦点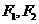 ,其中
,其中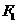 为
为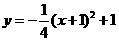 的焦点,两点A (-3,2) B (1,2)都在双曲线上,(1)求点
的焦点,两点A (-3,2) B (1,2)都在双曲线上,(1)求点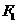 的坐标;(2)求点
的坐标;(2)求点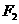 的轨迹方程,并画出轨迹的草图;(3)若直线
的轨迹方程,并画出轨迹的草图;(3)若直线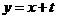 与
与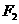 的轨迹方程有且只有一个公共点,求实数 t的取值范围。
的轨迹方程有且只有一个公共点,求实数 t的取值范围。
解答:(1)由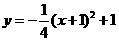 得:
得: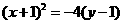
故 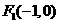
(2)设点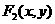
则又双曲线的定义得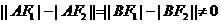
又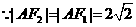
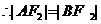 或
或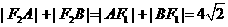
 点
点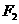 的轨迹是以
的轨迹是以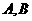 为焦点的椭圆
为焦点的椭圆

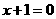 除去点
除去点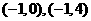 或
或 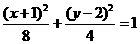 除去点
除去点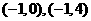 图略。
图略。
(3)联列: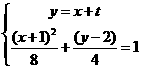 消去
消去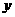 得
得
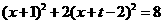 整理得:
整理得: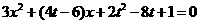
当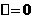 时 得
时 得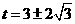 从图可知:
从图可知: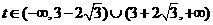 ,
,
又因为轨迹除去点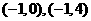 所以当直线过点
所以当直线过点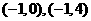 时也只有一个交点,即
时也只有一个交点,即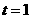 或5
或5
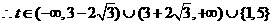
易错原因:(1)非标准方程求焦点坐标时计算易错;(2)求点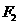 的轨迹时易少一种情况;(3)对有且仅有一个交点误认为方程只有一解。
的轨迹时易少一种情况;(3)对有且仅有一个交点误认为方程只有一解。
欢迎访问
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com