21．(本小题满分16分)

设函数，其图象在点处的切线

的斜率分别为．

(Ⅰ)求证：；

(Ⅱ)若函数的递增区间为，求的取值范围；

(Ⅲ)若当时(k是与无关的常数)，恒有，试求k的最小值．

20．(本小题满分14分)

已知数列的前n项和满足：(a为常数，且)．

(Ⅰ)求的通项公式；

(Ⅱ)设，若数列为等比数列，求a的值；

(Ⅲ)在满足条件(Ⅱ)的情形下，设，数列的前n项和为

T_n，求证：．

19．(本小题满分14分)

如图，在直四棱柱中，底面ABCD

是等腰梯形，，侧棱

．

(Ⅰ)证明：侧面；

(Ⅱ)设E是的中点，求异面直线与所成的角；

(Ⅲ)求二面角的大小．

18．(本小题满分14分)

假设某地区2007年教育投入400万元，其中有240万元用于义务教育，预计在今后

的若干年内，该地区每年教育投入平均比上一年增长10%．另外，每年教育投入中，

义务教育的投入资金均比上一年增加60万元，那么，到哪一年底，

(Ⅰ)该地区历年义务教育投入的累计资金(以2007年为累计的第一年)将首次不

少于3600万元？

(Ⅱ)当年用于义务教育的资金占该年教育投入资金的比例首次大于80%？(参考数据：)

17．(本小题满分12分)

如图，已知A是直线上一点，．

(Ⅰ)若抛物线C的顶点在坐标原点，焦点在坐标轴

上且经过点A，求抛物线C的标准方程；

(Ⅱ)若直线l是双曲线的一

条渐近线，且双曲线的右焦点在直线l上的射

影恰为点A，求双曲线的方程．

16．已知函数，其中表示不超过x的最大整数，如：，，　

　，若，则的值域为　　 ▲　　 ．

15．抛一枚均匀硬币，正、反面出现的概率都是，反复投掷，数列定义如下：

　，若，则事件“”

　的概率为　　 ▲　　 ．

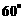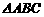14．已知球O和球面上A、B、C三点，OA与截面ABC所成的角为，且是边

　长为的等边三角形，则球O的表面积为　　　 ▲　　　 ．

13．已知x、y满足，则的最大值为　　 ▲　　　 ．

12．已知的展开式中，二项式系数之和为64，则它的二项展开式的中间项是

　　 ▲　　 ．