
题目列表(包括答案和解析)
6.(石庄中学)O为平面上的定点,A、B、C是平面上不共线的三点,若( 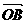 -
-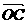 )·(
)·(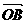 +
+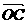 -2
-2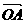 )=0,则DABC是( )
)=0,则DABC是( )
A.以AB为底边的等腰三角形 B.以BC为底边的等腰三角形
C.以AB为斜边的直角三角形 D.以BC为斜边的直角三角形
正确答案:B 错因:学生对题中给出向量关系式不能转化:2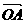 不能拆成(
不能拆成(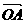 +
+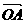 )。
)。
5.(石庄中学)已知向量  =(2cosj,2sinj),jÎ(
=(2cosj,2sinj),jÎ(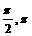 ),
), 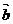 =(0,-1),则
=(0,-1),则  与
与 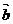 的夹角为( )
的夹角为( )
A.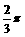 -j B.
-j B. +j C.j-
+j C.j- D.j
D.j
正确答案:A 错因:学生忽略考虑 与
与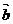 夹角的取值范围在[0,p]。
夹角的取值范围在[0,p]。
4.(石庄中学)若向量  =(cosa,sina) ,
=(cosa,sina) , 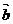 =
=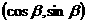 ,
,  与
与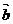 不共线,则
不共线,则 与
与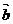 一定满足( )
一定满足( )
A.  与
与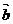 的夹角等于a-b B.
的夹角等于a-b B. ∥
∥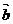
C.( +
+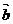 )^(
)^( -
-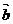 ) D.
) D.  ⊥
⊥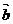
正确答案:C 错因:学生不能把 、
、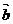 的终点看成是上单位圆上的点,用四边形法则来处理问题。
的终点看成是上单位圆上的点,用四边形法则来处理问题。
3.(石庄中学)已知O、A、B三点的坐标分别为O(0,0),A(3,0),B(0,3),是P线段AB上且 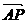 =t
=t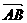 (0≤t≤1)则
(0≤t≤1)则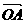 ·
·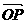 的最大值为 ( )
的最大值为 ( )
A.3 B.6 C.9 D.12
正确答案:C 错因:学生不能借助数形结合直观得到当|OP|cosa最大时,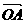 ·
·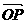 即为最大。
即为最大。
2.(如中)关于非零向量 和
和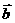 ,有下列四个命题:
,有下列四个命题:
(1)“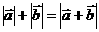 ”的充要条件是“
”的充要条件是“ 和
和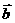 的方向相同”;
的方向相同”;
(2)“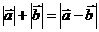 ” 的充要条件是“
” 的充要条件是“ 和
和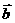 的方向相反”;
的方向相反”;
(3)“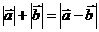 ” 的充要条件是“
” 的充要条件是“ 和
和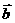 有相等的模”;
有相等的模”;
(4)“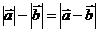 ” 的充要条件是“
” 的充要条件是“ 和
和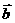 的方向相同”;
的方向相同”;
其中真命题的个数是 ( )
A 1 B 2 C 3 D 4
错误分析:对不等式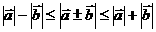 的认识不清.
的认识不清.
答案: B.
1.(如中)在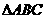 中,
中,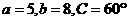 ,则
,则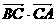 的值为
( )
的值为
( )
A 20
B 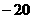 C
C 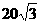 D
D 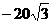
错误分析:错误认为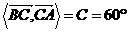 ,从而出错.
,从而出错.
答案: B
略解: 由题意可知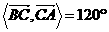 ,
,
故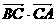 =
=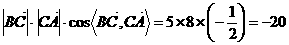 .
.
14.(江安中学)设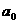 为常数,且
为常数,且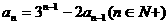
1)
证明对任意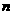 ≥
≥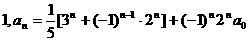 ;
;
2)
假设对任意n≥1有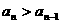 ,求
,求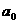 的取值范围
的取值范围
证明:①设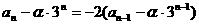
用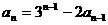 代入,解出:
代入,解出: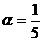
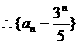 是公比为-2,首项为
是公比为-2,首项为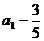 的等比数列。
的等比数列。
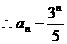
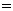
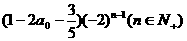 ,即
,即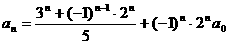
②若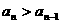
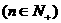 成立,特别取
成立,特别取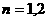 有
有
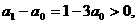
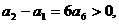
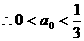
下面证明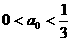 时,对任意
时,对任意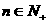 ,有
,有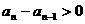
由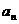 通项公式
通项公式
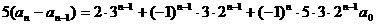 ,
,
i)
当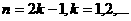 时,
时,
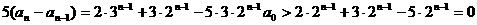
ii) 当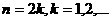 时,
时,
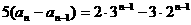 ≥0
≥0
故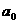 的取值范围为
的取值范围为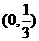
误解:①对于等比数列: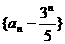 先构造出
先构造出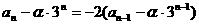 求
求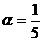 ,难度较大,若用数学归纳法证明同学容易想到。
,难度较大,若用数学归纳法证明同学容易想到。
②通过对n为奇数或为偶数的讨论找出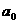 的取值范围有难度。
的取值范围有难度。
欢迎访问
13.(蒲中)已知数列{an}的前n项和为Sn,且满足an+2Sn·Sn-1=0(n≥2),a1=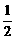 ,
,
(1)求证: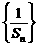 成等差数列;(2)求an的表达式。
成等差数列;(2)求an的表达式。
解:(1)当n≥2时,an=Sn-Sn-1,又an+2SnSn-1=0,∴Sn-Sn-1+SnSn-1=0
若Sn=0,则a1=S1=0与a1=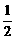 矛盾,∴Sn≠0,∴
矛盾,∴Sn≠0,∴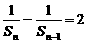 ,又
,又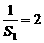
∴ 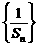 成等差数列。
成等差数列。
(2)由(1)知: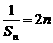 ,
,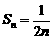
当n≥2时,an=-2SnSn-1=-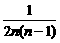 ,当n=1时,a1=
,当n=1时,a1=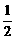
∴ 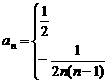

点评:本题易错点忽视公式an=Sn-Sn-1成立的条件“n≥2”,导致(2)的结果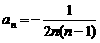
12.(薛中)已知数列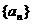 中,a1=8, a4=2且满足
中,a1=8, a4=2且满足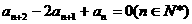 (1)求数列
(1)求数列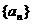 的
的
通项公式(2)设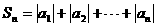 ,求Sn
,求Sn
(3)设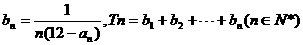 ,是否存在最大的整数m,使得对任意
,是否存在最大的整数m,使得对任意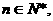 均有
均有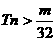 成立?若存在,求出m,若不存在,请说明理由。
成立?若存在,求出m,若不存在,请说明理由。
答案:(1)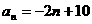
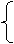 (2)Sn=
(2)Sn= 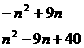
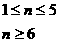
(3)由(1)可得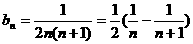
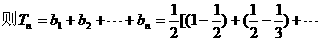
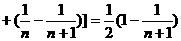 由Tn为关于n的增函数,故
由Tn为关于n的增函数,故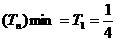 ,于是欲使
,于是欲使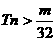 对
对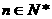 恒成立,则
恒成立,则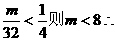 存在最大的整数m=7满足题意。
存在最大的整数m=7满足题意。
错因:对(2)中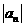 表达式不知进行分类讨论;对(3)忽视讨论Tn的单调性。
表达式不知进行分类讨论;对(3)忽视讨论Tn的单调性。
3、运算的能力
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com