2.若|a|=1, |b|=2, c=a+b，且c⊥a,则向量a与b的夹角是(　 )

　　 A.30°　　　　　　　　　　　 B.60°　　　　　　　　　　　 C.120°　　　　　　　　　　 D.150°

1.已知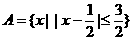，B={x|4x-x²>0}，则A∩B=(　 )

　　 A.(0，2]　　　　　　　　 B.[-1，0)　　　　　　　 C.[2，4)　　　　　　　　 D.[1，4)

22.(本小题满分14分)

已知函数f(x)=x³-3tx+m (x∈R, m和t为实数)是奇函数。

(I)求实数m的值和函数f(x)的图像与横轴的交点坐标；

(II)设g(x)=|f(x)|且x∈[-1,1],求g(x)的最大值F(t).

河南省郑州市2007年高中毕业班第三次质量预测

21.(本小题满分12分)

设抛物线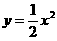的焦点为F，准线为l，过点F的直线斜率为k且与抛物线交于A，B两点，P在准线l上。

(I)当k=1且直线PA与PB相互垂直时，求点P的坐标；

(II)设P(k,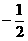),试问是否存在常数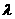，使等式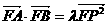恒成立？若存在，求出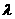的值；若不存在，说明理由。

20.(本小题满分12分)

已知数列{a_n}的各项均为正数，a₁=1,对任意n∈N^*，a_n+1=2a_n+1, b_n=log₂(a_n+1)都成立。

(I)求数列{a_n}, {b_n}的通项公式；

(II)证明：对于任意n∈N^*，都有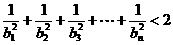成立。

19.(本小题满分12分)

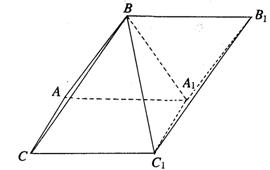
如图，斜三棱柱ABC-A₁B₁C₁的侧面AA₁C₁C是面积为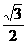的菱形。∠ACC₁为锐角，侧面ABB₁A₁⊥侧面AA₁C₁C，A₁B=AB=AC=1.

(I)求异面直线BB₁与AC所成的角；

(II)求侧面BCC₁B₁与侧面ACC₁A₁所成二面角的大小。

18.(本小题满分12分)

某运动员小马，欲取得08年奥运会参赛资格，需要参加三个阶段比赛，第一、第二阶段各有两个对手，必须都获胜，方可进入下一个阶段的比赛，第三阶段有三个对手，只要取胜两人就可以取得奥运会的参赛资格(先赢两场者第三场不用比赛)，每阶段获胜分别可得1万元、3万元、9万元的资金(不重复获奖)，小马对三个阶段每位运动员获胜的概率依次为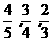，假定与每个选手比赛胜负相互独立。

(I)求小马通过第一阶段但未通过第二阶段的概率；

(II)求小马获得资金为3万元的概率。

17.(本小题满分12分)

已知函数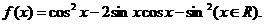

(I)画出函数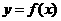在区间[0,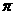]上的简图；

(II)说明函数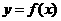的图象可由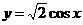的图象经过怎样的变换而得到。

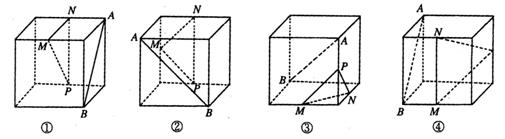
16.下面四个正方体图形中，A、B为正方体的两个项点，M、N、P分别为其所在棱的中点，能得出AB//平面MNP的图形序号是____________(写出所有符合要求的图形序号)

15.设等比数列{a_n}(n∈N^*)的首项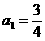，公比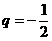，且a₁+a₃+…+a_2n-1=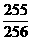，则n=____________.