
题目列表(包括答案和解析)
9.(磨中)设函数f(x)=logb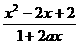 (b>0且b≠1),
(b>0且b≠1),
(1)求f(x)的定义域;
(2)当b>1时,求使f(x)>0的所有x的值。
解 (1)∵x2-2x+2恒正,
∴f(x)的定义域是1+2ax>0,
即当a=0时,f(x)定义域是全体实数。
当a>0时,f(x)的定义域是(-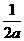 ,+∞)
,+∞)
当a<0时,f(x)的定义域是(-∞,-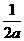 )
)
(2)当b>1时,在f(x)的定义域内,f(x)>0
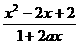 >1
>1 x2-2x+2>1+2ax
x2-2x+2>1+2ax
 x2-2(1+a)x+1>0
x2-2(1+a)x+1>0
其判别式Δ=4(1+a)2-4=4a(a+2)
(i)当Δ<0时,即-2<a<0时
∵x2-2(1+a)x+1>0
∴f(x)>0 x<-
x<-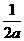
(ii)当Δ=0时,即a=-2或0时
若a=0,f(x)>0 (x-1)2>0
(x-1)2>0
 x∈R且x≠1
x∈R且x≠1
若a=-2,f(x)>0 (x+1)2>0
(x+1)2>0
 x<
x<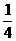 且x≠-1
且x≠-1
(iii)当△>0时,即a>0或a<-2时
方程x2-2(1+a)x+1=0的两根为
x1=1+a-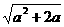 ,x2=1+a+
,x2=1+a+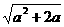
若a>0,则x2>x1>0>-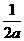
∴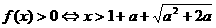 或
或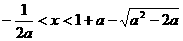
若a<-2,则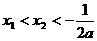
∴f(x)>0 x<1+a-
x<1+a-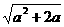 或1+a+
或1+a+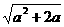 <x<-
<x<-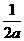
综上所述:当-2<a<0时,x的取值集合为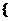 x|x<-
x|x<-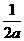
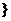
当a=0时,x∈R且x≠1,x∈R,当a=-2时: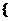 x|x<-1或-1<x<
x|x<-1或-1<x<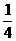
当a>0时,x∈ x|x>1+a+
x|x>1+a+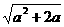 或-
或-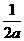 <x<1+a-
<x<1+a-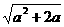
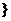
当a<-2时,x∈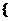 x|x<1+a-
x|x<1+a-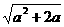 或1+a+
或1+a+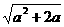 <x<-
<x<-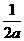
错误原因:解题时易忽视函数的定义域,不会合理分类。
8.(搬中)方程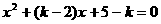 的两根都大于2,求实数
的两根都大于2,求实数 的取值范围。
的取值范围。
解:设方程的两根为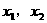 ,则必有
,则必有
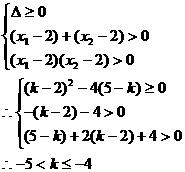
说明:此题易犯这样的错误:
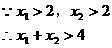
且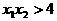
和判别式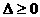 联立即得
联立即得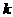 的范围
的范围
原因是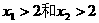 只是
只是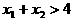 的充分条件
的充分条件
即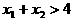 不能保证
不能保证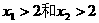 同时成立
同时成立
7.(搬中) 若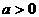 且
且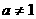 ,解不等式:
,解不等式:
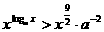
解:若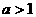 ,两边取以
,两边取以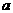 为底的对数
为底的对数
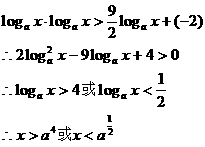
若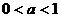 ,同样有,
,同样有,
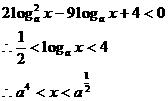
又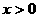
 当
当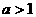 时不等式的解为
时不等式的解为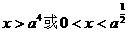
当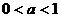 时不等式的解为
时不等式的解为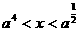
说明:此题易在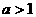 时的解中出错,容易忽略
时的解中出错,容易忽略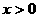 这个条件。解决对数问题要注意真数大于0的条件。
这个条件。解决对数问题要注意真数大于0的条件。
7.(搬中)解不等式: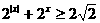 。
。
解:当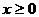 时,原不等式为
时,原不等式为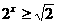
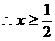
当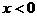 时,原不等式为
时,原不等式为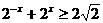
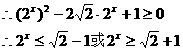
又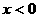
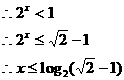
 原不等式的解为
原不等式的解为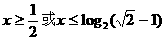
说明:此题易在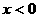 时
时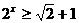 处出错,忽略了
处出错,忽略了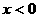 的前提。这提醒我们分段求解的结果要考虑分段的前提。
的前提。这提醒我们分段求解的结果要考虑分段的前提。
6.(搬中)求函数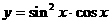 的最大值。
的最大值。
解: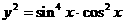
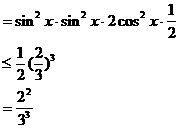
当且仅当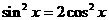
即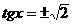 时,
时,
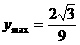 说明:此题容易这样做:
说明:此题容易这样做: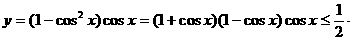
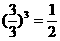 。但此时等号应满足条件
。但此时等号应满足条件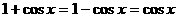 ,这样的
,这样的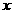 是不存在的,错误的原因是没有考虑到等号成立的条件。这一点在运用重要不等式时一定要引起我们高度的重视。
是不存在的,错误的原因是没有考虑到等号成立的条件。这一点在运用重要不等式时一定要引起我们高度的重视。
5.(搬中) 求函数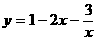 的极大值或极小值。
的极大值或极小值。
解:当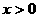 时,
时,
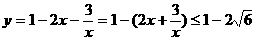
当且仅当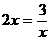
即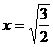 时,
时,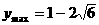
当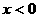 时,
时,
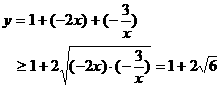
当且仅当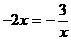
即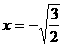 时,
时,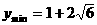
说明:此题容易漏掉对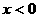 的讨论。不等式
的讨论。不等式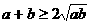 成立的前提是
成立的前提是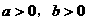 。
。
4.(搬中) 若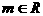 ,解关于
,解关于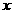 的不等式:
的不等式: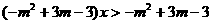 。
。
解:令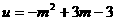
则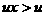
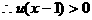
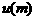 的判别式
的判别式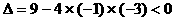
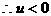 恒成立
恒成立
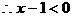
 原不等式的解为
原不等式的解为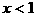
说明:此题容易由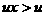 得出
得出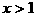 的错误结论。解有关不等式的问题,一定要注意含参数的表达式的符号,否则易出错误。
的错误结论。解有关不等式的问题,一定要注意含参数的表达式的符号,否则易出错误。
3.(搬中) 设 ,且
,且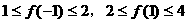 ,求
,求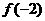 的取值范围。
的取值范围。
解:令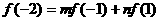
则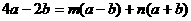
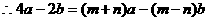
比较系数有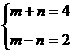
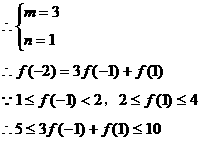
即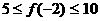
说明:此题极易由已知二不等式求出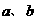 的范围,然后再求
的范围,然后再求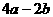 即
即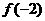 的范围,这种解法错在已知二不等式中的等号成立的条件不一定相同,它们表示的区域也不一定相同,用待定系数法则容易避免上述错误。
的范围,这种解法错在已知二不等式中的等号成立的条件不一定相同,它们表示的区域也不一定相同,用待定系数法则容易避免上述错误。
2.(如中)已知适合不等式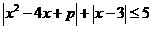 的x的最大值为3,求p的值。
的x的最大值为3,求p的值。
错解:对此不等式无法进行等价转化,不理解“x的最大值为3”的含义。
正解:因为x的最大值为3,故x-3<0,原不等式等价于 ,
,
即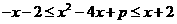 ,则
,则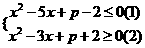
 ,
,
设(1)(2)的根分别为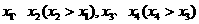 ,则
,则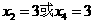
若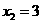 ,则9-15+p-2=0,p=8
,则9-15+p-2=0,p=8
若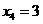 ,则9-9+p+2=0,p=-2
,则9-9+p+2=0,p=-2
当a=-2时,原方程组无解,则p=8
1.(如中)是否存在常数 c,使得不等式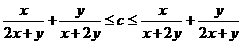 对任意正数 x,y恒成立?
对任意正数 x,y恒成立?
错解:证明不等式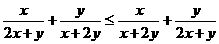 恒成立,故说明c存在。
恒成立,故说明c存在。
正解:令x=y得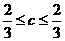 ,故猜想c=
,故猜想c=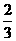 ,下证不等式
,下证不等式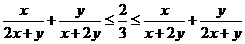 恒成立。
恒成立。
要证不等式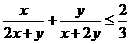 ,因为x,y是正数,即证3x(x+2y)+3y(2x+y)≤2(2 x+y)(x+2y),也即证
,因为x,y是正数,即证3x(x+2y)+3y(2x+y)≤2(2 x+y)(x+2y),也即证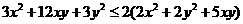 ,即2xy≤
,即2xy≤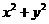 ,而此不等式恒成立,同理不等式
,而此不等式恒成立,同理不等式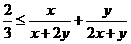 也成立,故存在c=
也成立,故存在c=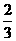 使原不等式恒成立。
使原不等式恒成立。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com