
题目列表(包括答案和解析)
4.
数列{a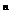 }中,已知a
}中,已知a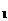 =1,当n≥2时a
=1,当n≥2时a =a
=a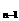 +2n-1,依次计算a
+2n-1,依次计算a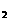 、a
、a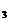 、a
、a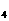 后,猜想a
后,猜想a 的表达式是_____。
的表达式是_____。
A. 3n-2
B. n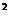 C. 3
C. 3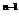 D. 4n-3
D. 4n-3
3. 某个命题与自然数n有关,若n=k (k∈N)时该命题成立,那么可推得n=k+1时该命题也成立。现已知当n=5时该命题不成立,那么可推得______。 (94年上海高考)
A.当n=6时该命题不成立 B.当n=6时该命题成立
C.当n=4时该命题不成立 D.当n=4时该命题成立
2.
用数学归纳法证明1+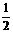 +
+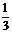 +…+
+…+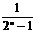 <n (n>1)时,由n=k (k>1)不等式成立,推证n=k+1时,左边应增加的代数式的个数是_____。
<n (n>1)时,由n=k (k>1)不等式成立,推证n=k+1时,左边应增加的代数式的个数是_____。
A. 2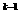 B. 2
B. 2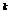 -1
C. 2
-1
C. 2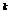 D. 2
D. 2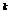 +1
+1
数学归纳法是一个递推的数学论证方法,论证的第一步是证明命题在n=1(或n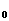 )时成立,这是递推的基础;第二步是假设在n=k时命题成立,再证明n=k+1时命题也成立,这是递推的依据。实际上它使命题的正确性突破了有限,达到无限。证明时,关键是k+1步的推证,要有目标意识。
)时成立,这是递推的基础;第二步是假设在n=k时命题成立,再证明n=k+1时命题也成立,这是递推的依据。实际上它使命题的正确性突破了有限,达到无限。证明时,关键是k+1步的推证,要有目标意识。
Ⅰ、再现性题组:
1.
用数学归纳法证明(n+1)(n+2)…(n+n)=2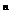 ·1·2…(2n-1)
(n∈N),从“k到k+1”,左端需乘的代数式为_____。
·1·2…(2n-1)
(n∈N),从“k到k+1”,左端需乘的代数式为_____。
A. 2k+1
B. 2(2k+1)
C. 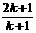 D.
D. 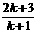
10.
设s>1,t>1,m∈R,x=log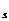 t+log
t+log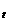 s,y=log
s,y=log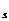
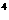 t+log
t+log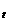
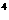 s+m(log
s+m(log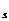
 t+log
t+log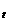
 s),
s),
① 将y表示为x的函数y=f(x),并求出f(x)的定义域;
② 若关于x的方程f(x)=0有且仅有一个实根,求m的取值范围。
9.
设二次函数f(x)=Ax +Bx+C,给定m、n(m<n),且满足A
+Bx+C,给定m、n(m<n),且满足A [(m+n)
[(m+n) + m
+ m n
n ]+2A[B(m+n)-Cmn]+B
]+2A[B(m+n)-Cmn]+B +C
+C =0 。
=0 。
① 解不等式f(x)>0;
② 是否存在一个实数t,使当t∈(m+t,n-t)时,f(x)<0 ?若不存在,说出理由;若存在,指出t的取值范围。
8.
已知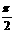 〈β<α〈
〈β<α〈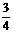 π,cos(α-β)=
π,cos(α-β)=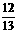 ,sin(α+β)=-
,sin(α+β)=-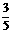 ,求sin2α的值。(92年高考题)
,求sin2α的值。(92年高考题)
7.
若x>-1,则f(x)=x +2x+
+2x+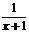 的最小值为___________。
的最小值为___________。
6.
设F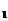 和F
和F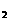 为双曲线
为双曲线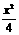 -y
-y =1的两个焦点,点P在双曲线上且满足∠F
=1的两个焦点,点P在双曲线上且满足∠F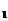 PF
PF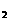 =90°,则△F
=90°,则△F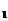 PF
PF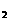 的面积是_________。
的面积是_________。
5. 化简:2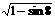 +
+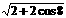 的结果是_____。
的结果是_____。
A. 2sin4 B. 2sin4-4cos4 C. -2sin4 D. 4cos4-2sin4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com