
题目列表(包括答案和解析)
2、②运算的技巧
12.(城西中学)设二次函数f(x)=x2+x,当x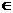 [n,n+1](n
[n,n+1](n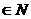 +)时,f(x)的所有整数值的个数为g(n).
+)时,f(x)的所有整数值的个数为g(n).
(1) 求g(n)的表达式;
(2)
设an=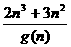 ( n
( n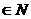 +),Sn=a1-a2+a3-a4+…+(-1)n-1an,求Sn;
+),Sn=a1-a2+a3-a4+…+(-1)n-1an,求Sn;
(3)
设bn=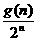 ,Tn=b1+b2+…+bn,
若Tn<L( L
,Tn=b1+b2+…+bn,
若Tn<L( L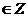 ),求L的最小值。
),求L的最小值。
正确答案:(1)当x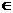 [n,n+1](n
[n,n+1](n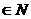 +)时,函数f(x)=x2+x的值随x的增大而增大,则f(x)的值域为
+)时,函数f(x)=x2+x的值随x的增大而增大,则f(x)的值域为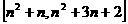 (n
(n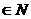 +)
+)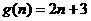 (n
(n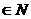 +)
+)
(2)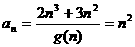
① 当n为偶数时
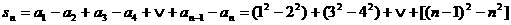
=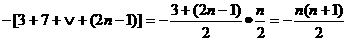
②当n为奇数时
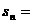
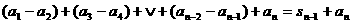
=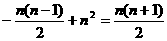
∴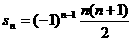
(3)由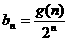 ,得
,得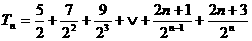 ①
①
①×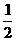 得:
得: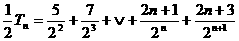 ②
②
①-②得 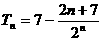
则由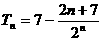 ﹤L( L
﹤L( L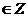 ),L的最小值为7。
),L的最小值为7。
错因:1、①中整数解的问题
11.(城西中学)学校餐厅每天供应1000名学生用餐,每星期一有A、B两样特色菜可供选择(每个学生都将从二者中选一),调查资料表明,凡是在本周星期一选A菜的,下周星期一会有20%改选B,而选B菜的,下周星期一则有30%改选A,若用A 、B
、B 分别表示在第n个星期一选A、B菜的人数。(1)试以A
分别表示在第n个星期一选A、B菜的人数。(1)试以A 表示A
表示A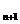 ;(2)若A
;(2)若A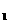 =200,求{A
=200,求{A }的通项公式;(3)问第n个星期一时,选A与选B的人数相等?
}的通项公式;(3)问第n个星期一时,选A与选B的人数相等?
正确答案:(1)由题可知,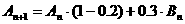 ,又
,又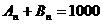 ;
;
所以整理得: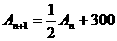 。(2)若A
。(2)若A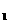 =200,且
=200,且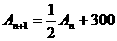 ,则设
,则设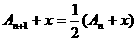 则
则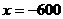 ,
,
∴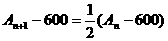 即{A
即{A -600}可以看成是首项为-400,公比为
-600}可以看成是首项为-400,公比为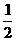 的等比数列。
的等比数列。
∴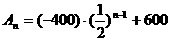 ;(3)∵
;(3)∵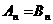 ,又
,又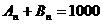 则
则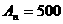 , 由
, 由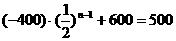 得
得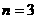 。即第3个星期一时,选A与选B的人数相等。
。即第3个星期一时,选A与选B的人数相等。
错因:不会处理非等差非等比数列。
10.(磨中)求和(x+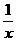 )2+(x2+
)2+(x2+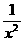 )2+……(xn+
)2+……(xn+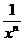 )2
)2
正确答案:当x2=1时 Sn=4n
当x2≠1时 Sn=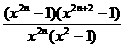 +2n
+2n
错误原因:应用等比数列求和时未考虑公比q是否为1
9.(磨中)数列{an}的前n项和Sn=n2-7n-8求数列通项公式
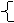 正确答案:an= -14 n=1
正确答案:an= -14 n=1
2n-8 n≥2
错误原因: n≥2时,an=Sn-Sn-1 但n=1时,不能用此式求出a1
8.(磨中) 已知函数f(x)= -Sin2x-aSinx+b+1的最大值为0,最小值-4 ,若实数a>0,求a、b的值。
正确答案:a=2 b= -2
错误原因:忽略对区间的讨论。
7.(磨中)已知数列{an}的前n项和Sn=n2-16n-6,求数列{|an|}的前n项和Sn’
 正确答案:Sn’= -n2+16n+6 n≤8时
正确答案:Sn’= -n2+16n+6 n≤8时
n2-16n+134 n>8时
错误原因:运用或推导公式时,只考虑一般情况,忽视特殊情况,导致错解。
6.(搬中)求和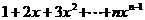 。
。
解:若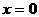
则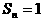
若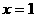
则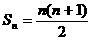
若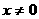
且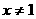
令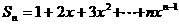
则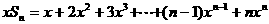
两式相减得
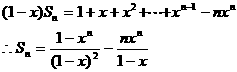
说明:此题易忽略前两种情况。数列求和时,若含有字母,一定要考虑相应的特殊情况。
5.(搬中)等比数列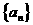 的前
的前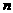 项和为
项和为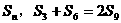 ,求公比
,求公比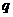 。
。
解:若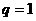
则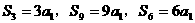
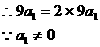
 矛盾
矛盾
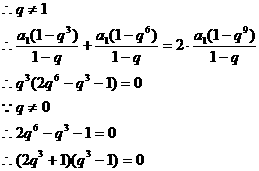
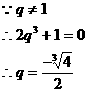
说明:此题易忽略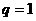 的情况,在等比数列求和时要分公比
的情况,在等比数列求和时要分公比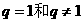 两种情况进行讨论。
两种情况进行讨论。
4.(搬中) 已知数列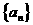 的前
的前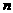 项和
项和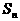 满足
满足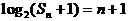 ,求数列
,求数列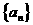 的通项公式。
的通项公式。
解: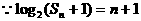
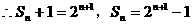
当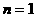 时,
时,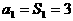
当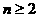 时,
时,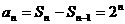
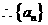 的通项公式为
的通项公式为
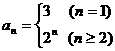
说明:此题易忽略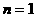 的情况。
的情况。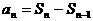 应满足条件
应满足条件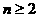 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com