
题目列表(包括答案和解析)
4. 椭圆x -2ax+3y
-2ax+3y +a
+a -6=0的一个焦点在直线x+y+4=0上,则a=_____。
-6=0的一个焦点在直线x+y+4=0上,则a=_____。
A. 2 B. -6 C. -2或-6 D. 2或6
3. 已知x、y∈R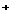 ,且满足x+3y-1=0,则函数t=2
,且满足x+3y-1=0,则函数t=2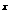 +8
+8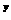 有_____。
有_____。
A.最大值2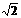 B.最大值
B.最大值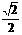 C.最小值2
C.最小值2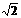 B.最小值
B.最小值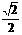
2. α、β是方程x -2ax+a+6=0的两实根,则(α-1)
-2ax+a+6=0的两实根,则(α-1) +(β-1)
+(β-1) 的最小值是_____。
的最小值是_____。
A. -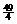 B. 8 C. 18 D.不存在
B. 8 C. 18 D.不存在
1. 函数y=(x-a) +(x-b)
+(x-b) (a、b为常数)的最小值为_____。
(a、b为常数)的最小值为_____。
A. 8 B. 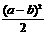 C.
C. 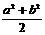 D.最小值不存在
D.最小值不存在
5.
已知方程x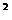 +(a-2)x+a-1=0的两根x
+(a-2)x+a-1=0的两根x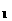 、x
、x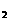 ,则点P(x
,则点P(x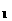 ,x
,x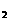 )在圆x
)在圆x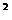 +y
+y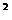 =4上,则实数a=_____。
=4上,则实数a=_____。
Ⅱ、示范性题组:
例1. 已知长方体的全面积为11,其12条棱的长度之和为24,则这个长方体的一条对角线长为_____。
A. 2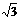 B.
B. 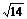 C.
5
D. 6
C.
5
D. 6
[分析]
先转换为数学表达式:设长方体长宽高分别为x,y,z,则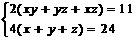 ,而欲求对角线长
,而欲求对角线长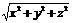 ,将其配凑成两已知式的组合形式可得。
,将其配凑成两已知式的组合形式可得。
[解]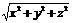 =…
=…
例2. 设方程x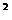 +kx+2=0的两根为p、q,若(
+kx+2=0的两根为p、q,若(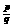 )
)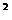 +(
+(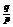 )
)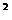 ≤7成立,求k的取值范围。
≤7成立,求k的取值范围。
[解] 由韦达定理得:p+q=-k,pq=2 ,
(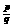 )
)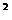 +(
+(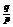 )
)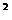 =
=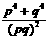 =
=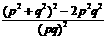 =
=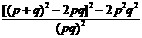 =
=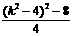 ≤7, 解得k≤-
≤7, 解得k≤-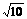 或k≥
或k≥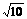 。
。
又
∵p、q为方程两实根, ∴ Δ=k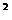 -8≥0
-8≥0
∴k的取值范围是:-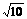 ≤k≤-
≤k≤-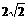 或者
或者 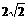 ≤k≤
≤k≤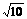
[注] 实系数一元二次方程问题,注意Δ,恰当运用韦达定理;由已知的不等式联想到配方,表示成p+q与pq的组合式。
例3. 设非零复数a、b满足a +ab+b
+ab+b =0,求(
=0,求(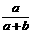 )
) +(
+(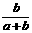 )
) 。
。
[分析]
对已知式可以联想:变形为(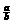 )
)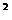 +(
+(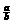 )+1=0,则
)+1=0,则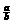 =ω (ω为1的立方虚根);或配方为(a+b)
=ω (ω为1的立方虚根);或配方为(a+b) =ab 。则代入所求式即得。
=ab 。则代入所求式即得。
[解]
[注] 配方,简化表达式;巧用1的立方虚根,计算高次幂;活用ω的性质。
[另解]
解出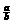 =…后,用三角形式完成后面的运算:
=…后,用三角形式完成后面的运算:
Ⅲ、巩固性题组:
4.
函数y=log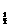 (-2x
(-2x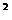 +5x+3)的单调递增区间是_____。
+5x+3)的单调递增区间是_____。
A. (-∞, 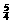 ]
B. [
]
B. [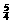 ,+∞) C. (-
,+∞) C. (-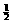 ,
,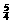 ] D. [
] D. [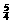 ,3)
,3)
3.
已知sin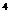 α+cos
α+cos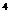 α=1,则sinα+cosα的值为______。
α=1,则sinα+cosα的值为______。
A. 1 B. -1 C. 1或-1 D. 0
2.
方程x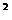 +y
+y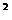 -4kx-2y+5k=0表示圆的充要条件是_____。
-4kx-2y+5k=0表示圆的充要条件是_____。
A. 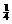 <k<1 B. k<
<k<1 B. k<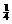 或k>1 C. k∈R
D. k=
或k>1 C. k∈R
D. k=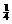 或k=1
或k=1
配方法是对数学式子进行一种定向变形(配成“完全平方”)的技巧,通过配方找到已知和未知的联系,从而化繁为简。何时配方,需要我们适当预测,并且需要“凑(拆)”而“配”。
Ⅰ、再现性题组:
1.
在正项等比数列{a }中,a
}中,a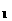 sa
sa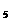 +2a
+2a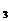 sa
sa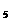 +a
+a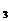 ža
ža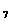 =25,则 a
=25,则 a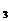 +a
+a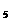 =_______。
=_______。
22.(14分)已知椭圆C的焦点是F1(-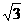 ,0)、F2(
,0)、F2(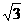 ,0),点F1到相应的准线的距离为
,0),点F1到相应的准线的距离为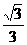 ,过F2点且倾斜角为锐角的直线l与椭圆C交于A、B两点,使得|F2B|=3|F2A|.
,过F2点且倾斜角为锐角的直线l与椭圆C交于A、B两点,使得|F2B|=3|F2A|.
(1)求椭圆C的方程;(2)求直线l的方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com