
题目列表(包括答案和解析)
7.求函数解析式的常用方法:
(1)待定系数法――已知所求函数的类型(二次函数的表达形式有三种:一般式: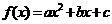 ;顶点式:
;顶点式: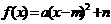 ;零点式:
;零点式: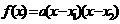 ,要会根据已知条件的特点,灵活地选用二次函数的表达形式)。
,要会根据已知条件的特点,灵活地选用二次函数的表达形式)。
(2)代换(配凑)法――已知形如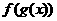 的表达式,求
的表达式,求 的表达式。这里需值得注意的是所求解析式的定义域的等价性,即
的表达式。这里需值得注意的是所求解析式的定义域的等价性,即 的定义域应是
的定义域应是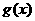 的值域。
的值域。
(3)方程的思想――已知条件是含有 及另外一个函数的等式,可抓住等式的特征对等式的进行赋值,从而得到关于
及另外一个函数的等式,可抓住等式的特征对等式的进行赋值,从而得到关于 及另外一个函数的方程组。
及另外一个函数的方程组。
9.(1)函数 是奇函数,定义域是
是奇函数,定义域是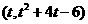 ,则
,则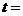
(2)判断函数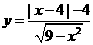 的奇偶性____(3)判断
的奇偶性____(3)判断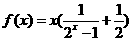 的奇偶性___.
的奇偶性___.
(4)若定义在R上的偶函数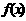 在
在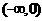 上是减函数,且
上是减函数,且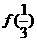 =2,则不等式
=2,则不等式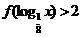 的解集为
的解集为
(5) 判断下列函数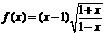 的奇偶性
(6)判断下列函数
的奇偶性
(6)判断下列函数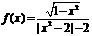 奇偶性
奇偶性
(7) 判断下列各函数f(x)=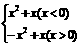 的奇偶性: (8)若
的奇偶性: (8)若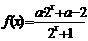 为奇函数,则实数
为奇函数,则实数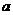 =
=
(9)若将函数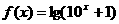 ,表示成一个奇函数
,表示成一个奇函数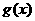 和一个偶函数
和一个偶函数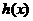 之和,则
之和,则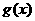 =____
=____
友 情 提 示 6.分段函数的概念。分段函数是在其定义域的不同子集上,分别用几个不同的式子来表示对应关系的函数,它是一类较特殊的函数。在求分段函数的值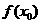 时,一定首先要判断
时,一定首先要判断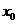 属于定义域的哪个子集,然后再代相应的关系式;分段函数的值域应是其定义域内不同子集上各关系式的取值范围的并集。
属于定义域的哪个子集,然后再代相应的关系式;分段函数的值域应是其定义域内不同子集上各关系式的取值范围的并集。
8. (1)函数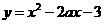 在区间[1, 2]上存在反函数的充要条件是
在区间[1, 2]上存在反函数的充要条件是
A、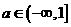 B、
B、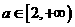 C、
C、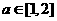 D、
D、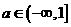
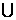
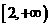
(2)函数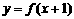 的反函数不是
的反函数不是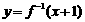 ,而是
。
,而是
。
(3)设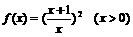 .求
.求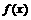 的反函数
的反函数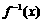
(4)已知函数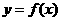 的图象过点(1,1),那么
的图象过点(1,1),那么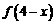 的反函数的图象一定经过点____
的反函数的图象一定经过点____
(5)已知函数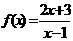 ,若函数
,若函数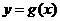 与
与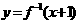 的图象关于直线
的图象关于直线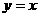 对称,求
对称,求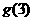 的值
的值
(6)已知函数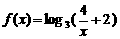 ,则方程
,则方程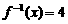 的解
的解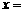 ______;
______;
(7)设函数f(x)的图象关于点(1,2)对称,且存在反函数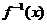 ,f (4)=0,则
,f (4)=0,则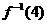 =
=
(8)已知函数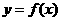 的图象
的图象
过(1,2),则函数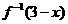 的图象一定经过
的图象一定经过
7.1)已知二次函数 的对称轴为
的对称轴为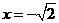 ,截
,截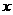 轴上的弦长为
轴上的弦长为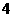 ,且过点
,且过点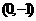 ,求函数的解析式
.
,求函数的解析式
.
(2)已知二次函数 的二次项系数为
的二次项系数为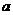 ,且方程
,且方程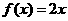 的解分别是-1,3,若方程
的解分别是-1,3,若方程 有两个相等的实数根,求
有两个相等的实数根,求 的解析式
的解析式
(3)已知 求
求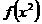 的解析式
;
的解析式
;
(4)已知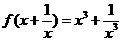 ,求
,求 (5)已知
(5)已知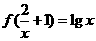 ,求
,求
(5)已知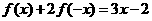 ,求
,求 的解析式
;
的解析式
;
(6)已知 是奇函数,
是奇函数,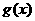 是偶函数,且
是偶函数,且 +
+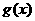 =
=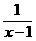 ,则
,则 = __。
= __。
6.(1)设函数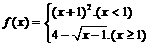 ,则使得
,则使得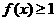 的自变量
的自变量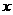 的取值范围是__________;
的取值范围是__________;
(2)已知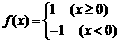 ,则不等式
,则不等式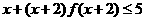 的解集是________
的解集是________
(3)已知函数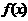 ,满足
,满足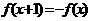 ,当
,当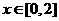
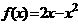 。求函数
。求函数 在
在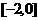 上的解析式
上的解析式
(4)函数 是偶函数,
是偶函数,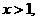
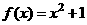 。求
。求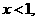
 得表达式
。
得表达式
。
(5)已知奇函数 ,当
,当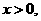
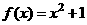 。求函数
。求函数 的解析式
的解析式
1.(1)A;(2)(2,-1);(3)12;2.(1)0或1;(2)2(3).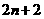 个3. 9;4.(1)
个3. 9;4.(1)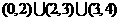 ;
;
(2)B.(3)(B)(4) [1,5](5){x|2<x<3};(6){x|1<x<3}(7) [2, 5]5(1)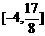 (2)
(2)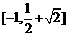
(3)(0,1);(4)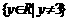 .(5)
.(5)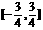 。(6)
。(6)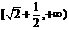 。(7){y| y>1 或y
。(7){y| y>1 或y
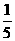 且y
且y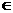 R}.
R}.
(8)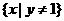 (9)
(9)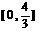 .(10)
.(10)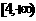 (11)
(11)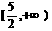 。(12){y| y
。(12){y| y 1且y
1且y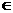 R}.(13)
R}.(13)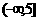 .(14)
.(14)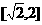 。
。
(15)(答:-48)
函数基本概念回归课本复习材料2
今天,我怕谁之四
5.求函数值域(最值)的方法:
(1)配方法――二次函数(二次函数在给出区间上的最值有两类:一是求闭区间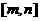 上的最值;二是求区间定(动),对称轴动(定)的最值问题。求二次函数的最值问题,勿忘数形结合,注意“两看”:一看开口方向;二看对称轴与所给区间的相对位置关系),
上的最值;二是求区间定(动),对称轴动(定)的最值问题。求二次函数的最值问题,勿忘数形结合,注意“两看”:一看开口方向;二看对称轴与所给区间的相对位置关系),
(2)换元法――通过换元把一个较复杂的函数变为简单易求值域的函数,其函数特征是函数解析式含有根式或三角函数公式模型,
(3)函数有界性法――直接求函数的值域困难时,可以利用已学过函数的有界性,来确定所求函数的值域,最常用的就是三角函数的有界性,
(4)单调性法――利用一次函数,反比例函数,指数函数,对数函数等函数的单调性,
(5)数形结合法――函数解析式具有明显的某种几何意义,如两点的距离、直线斜率、等等,
注意:求两点距离之和时,要将函数式变形,使两定点在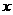 轴的两侧,而求两点距离之差时,则要使两定点在
轴的两侧,而求两点距离之差时,则要使两定点在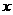 轴的同侧。
轴的同侧。
(6)判别式法――对分式函数(分子或分母中有一个是二次)都可通用,但这类题型有时也可以用其它方法进行求解,不必拘泥在判别式法上,也可先通过部分分式后,再利用均值不等式:
①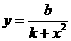 型,可直接用不等式性质,②
型,可直接用不等式性质,②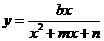 型,先化简,再用均值不等式,③
型,先化简,再用均值不等式,③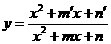 型,通常用判别式法;④
型,通常用判别式法;④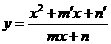 型,可用判别式法或均值不等式法,
型,可用判别式法或均值不等式法,
(7)不等式法――利用基本不等式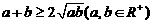 求函数的最值,其题型特征解析式是和式时要求积为定值,解析式是积时要求和为定值,不过有时须要用到拆项、添项和两边平方等技巧。
求函数的最值,其题型特征解析式是和式时要求积为定值,解析式是积时要求和为定值,不过有时须要用到拆项、添项和两边平方等技巧。
(8)导数法――一般适用于高次多项式函数
提醒:(1)求函数的定义域、值域时,你按要求写成集合形式了吗?
(2)函数的最值与值域之间有何关系?
4. 求函数定义域的常用方法(在研究函数问题时要树立定义域优先的原则):
(1)根据解析式要求如偶次根式的被开方大于零,分母不能为零,对数 中
中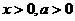 且
且 ,三角形中
,三角形中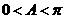 , 最大角
, 最大角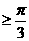 ,最小角
,最小角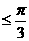 等。(2)根据实际问题的要求确定自变量的范围。
等。(2)根据实际问题的要求确定自变量的范围。
(3)复合函数的定义域:若已知 的定义域为
的定义域为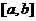 ,其复合函数
,其复合函数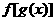 的定义域由不等式
的定义域由不等式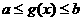 解出即可;若已知
解出即可;若已知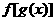 的定义域为
的定义域为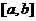 ,求
,求 的定义域,相当于当
的定义域,相当于当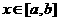 时,求
时,求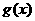 的值域(即
的值域(即 的定义域)。
的定义域)。
3. 同一函数的概念。构成函数的三要素是定义域,值域和对应法则。而值域可由定义域和对应法则唯一确定,因此当两个函数的定义域和对应法则相同时,它们一定为同一函数。
2.函数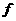 : A
: A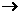 B是特殊的映射。特殊在定义域A和值域B都是非空数集!据此可知函数图像与
B是特殊的映射。特殊在定义域A和值域B都是非空数集!据此可知函数图像与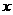 轴的垂线至多有一个公共点,但与
轴的垂线至多有一个公共点,但与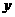 轴垂线的公共点可能没有,也可能有任意个。
轴垂线的公共点可能没有,也可能有任意个。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com