
题目列表(包括答案和解析)
5.设函数f(x)=x3-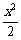 -2x+5.若对任意x∈[-1,2],都有f(x)>m,则实数m的取值范围是________.
-2x+5.若对任意x∈[-1,2],都有f(x)>m,则实数m的取值范围是________.
解析: (x)=3x2-x-2=0,x=1,-
(x)=3x2-x-2=0,x=1,-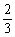 ,
,
f(-1)=5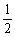 ,f(-
,f(-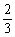 )=5
)=5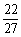 ,f(1)=3
,f(1)=3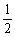 ,f(2)=7.
,f(2)=7.
∴m<3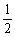 .
.
答案:m∈(-∞,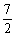 )
)
●典例剖析
[例1] (2004年天津,20)已知函数f(x)=ax3+bx2-3x在x=±1处取得极值.
(1)讨论f(1)和f(-1)是函数f(x)的极大值还是极小值;
(2)过点A(0,16)作曲线y=f(x)的切线,求此切线方程.
剖析:(1)分析x=±1处的极值情况,关键是分析x=±1左右 (x)的符号.
(x)的符号.
(2)要分清点A(0,16)是否在曲线上.
解:(1) (x)=3ax2+2bx-3,依题意,
(x)=3ax2+2bx-3,依题意, (1)=
(1)= (-1)=0,即
(-1)=0,即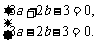
解得a=1,b=0.
∴f(x)=x3-3x, (x)=3x2-3=3(x+1)(x-1).
(x)=3x2-3=3(x+1)(x-1).
令 (x)=0,得x=-1,x=1.
(x)=0,得x=-1,x=1.
若x∈(-∞,-1)∪(1,+∞),则 (x)>0,
(x)>0,
故f(x)在(-∞,-1)上是增函数,f(x)在(1,+∞)上是增函数.
若x∈(-1,1),则 (x)<0,故f(x)在(-1,1)上是减函数.
(x)<0,故f(x)在(-1,1)上是减函数.
所以f(-1)=2是极大值,f(1)=-2是极小值.
(2)曲线y=x3-3x,点A(0,16)不在曲线上,设切点M(x0,y0),则y0=x03-3x.
∵ (x0)=3x02-3,
(x0)=3x02-3,
∴切线方程为y-y0=3(x02-1)(x-x0).
代入A(0,16)得16-x03+3x0=3(x02-1)(0-x0).
解得x0=-2,∴M(-2,-2),切线方程为9x-y+16=0.
评述:过已知点求切线,当点不在曲线上时,求切点的坐标成了解题的关键.
[例2] (2004年天津,21)已知函数f(x)=ax3+cx+d(a≠0)是R上的奇函数,当x=1时,f(x)取得极值-2.
(1)求f(x)的单调区间和极大值;
(2)证明:对任意x1、x2∈(-1,1),不等式|f(x1)-f(x2)|<4恒成立.
剖析:∵x∈R且f(x)是奇函数,
∴f(0)=0.
又x=1是极值点,∴ (1)=0,由此可得函数的解析式.
(1)=0,由此可得函数的解析式.
(1)解:由奇函数定义,
应有f(-x)=-f(x),x∈R,-ax3-cx+d=-ax3-cx-d,∴d=0.
因此f(x)=ax3+cx, (x)=3ax2+c.
(x)=3ax2+c.
由题意知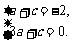
解得a=1,c=-3.
∴f(x)=x3-3x, (x)=3x3-3=3(x-1)(x+1),
(x)=3x3-3=3(x-1)(x+1), (-1)=
(-1)= (1)=0.
(1)=0.
当x∈(-∞,-1)时, (x)>0,故f(x)在单调区间(-∞,-1)上是增函数,
(x)>0,故f(x)在单调区间(-∞,-1)上是增函数,
当x∈(-1,1)时, (x)<0,故f(x)在单调区间(-1,1)上是减函数,
(x)<0,故f(x)在单调区间(-1,1)上是减函数,
当x∈(1,+∞)时, (x)>0,故f(x)在单调区间(1,+∞)上是增函数.
(x)>0,故f(x)在单调区间(1,+∞)上是增函数.
∴(-∞,-1)和(1,+∞)为增区间;
(-1,1)为减区间,x=-1时,f(-1)=2为极大值,
x=-1时,f(1)=-2为极小值.
(2)f(-1)=2,f(1)=-2.
∵f(x)在(-1,1)上是减函数,
∴对任意x1、x2∈(-1,1),有-2<f(x1)<2,-2<f(x2)<2,
-4<f(x1)-f(x2)<4,即|f(x1)-f(x2)|<4.
评述:由奇函数定义可知当x=0时,则有f(0)=0,即函数过原点.对于本题的第(2)问,用数形结合法较为直观.
[例3] 设函数f(x)=x3+mx2+nx+p在(-∞,0]上是增函数,在[0,2]上是减函数,x=2是方程f(x)=0的一个根.
(1)求n的值;
(2)求证:f(1)≥2.
剖析:由题知x=0是极值点,那么另一个极值点在哪儿呢?是x=2吗?不一定.会在x=2的哪一侧呢?
解:(1) (x)=3x2+2mx+n.
(x)=3x2+2mx+n.
∵f(x)在(-∞,0]上是增函数,在[0,2]上是减函数,
∴当x=0时,f(x)取到极大值.
∴ (0)=0.∴n=0.
(0)=0.∴n=0.
(2)∵f(2)=0,∴p=-4(m+2),
 (x)=3x2+2mx=0的两个根分别为x1=0,x2=-
(x)=3x2+2mx=0的两个根分别为x1=0,x2=-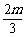 ,
,
∵函数f(x)在[0,2]上是减函数,
∴x2=-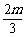 ≥2.∴m≤-3.
≥2.∴m≤-3.
∴f(1)=m+p+1=m-4(m+2)+1=-7-3m≥2.
评述:此题学生往往错误地认为x=2是另一个极值点.再证f(1)≥2时,首先将f(1)化成关于m的式子,知道m的范围,便可证之.
[例4] 对于函数y=f(x)(x∈D)若同时满足下列两个条件,则称f(x)为D上的闭函数.
①f(x)在D上为单调函数;
②存在闭区间[a,b]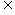 D,使f(x)在[a,b]上的值域也是[a,b].
D,使f(x)在[a,b]上的值域也是[a,b].
(1)求闭函数y=-x3符合上述条件的区间[a,b];
(2)若f(x)=x3-3x2-9x+4,判断f(x)是否为闭函数.
剖析:这是个知识迁移题,这类问题一般是考查学生的类比猜想能力、探索问题的能力.
解:(1)∵y=-x3,∴y′=-3x2≤0.
∴函数y=-x3为减函数.
故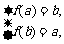 即
即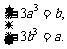
∴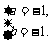 所求闭区间为[-1,1].
所求闭区间为[-1,1].
(2) (x)=3x2-6x-9.
(x)=3x2-6x-9.
由 (x)≥0,得x≥3或x≤-1.
(x)≥0,得x≥3或x≤-1.
由 (x)≤0,得-1≤x≤3.
(x)≤0,得-1≤x≤3.
∴f(x)在定义域内不是单调函数.故f(x)不是闭函数.
评述:这类问题是近年高考命题的一个亮点,很能考查学生的分析问题、探索问题的潜在的能力.
●闯关训练
夯实基础
4.已知函数y=x3+ax2+bx+27在x=-1处有极大值,在x=3处有极小值,则a+b=________.
解析:y′=3x2+2ax+b,-1、3是3x2+2ax+b=0的两根,∴a=-3,b=-9.
答案:-12
3.已知f(x)=2x3-6x2+m(m为常数)在[-2,2]上有最大值3,那么此函数在[-2,2]上的最小值是
A.-37 B.-29
C.-5 D.以上都不对
解析: (x)=6x(x-2),f(x)在(-2,0)上为增函数,在(0,2)上为减函数的,x=0时,f(x)=m最大.
(x)=6x(x-2),f(x)在(-2,0)上为增函数,在(0,2)上为减函数的,x=0时,f(x)=m最大.
∴m=3,f(-2)=-37,f(2)=-5.
答案:A
2.函数f(x)=x3-3bx+3b在(0,1)内有极小值,则
A.0<b<1 B.b<1
C.b>0
D.b<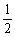
解析:  (x)=3x2-3b,当b>0,0<
(x)=3x2-3b,当b>0,0<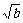 <1时,适合题意.
<1时,适合题意.
答案:A
1.函数f(x)=x3-3x+1在闭区间[-3,0]上的最大值、最小值分别是
A.1,-1 B.1,-17
C.3,-17 D.9,-19
解析: (x)=3x2-3=0,x=±1,f(-3)=-17,f(0)=1,f(1)=-1,f(-1)=3.
(x)=3x2-3=0,x=±1,f(-3)=-17,f(0)=1,f(1)=-1,f(-1)=3.
答案:C
2.设y=f(x)是一多项式函数,比较函数在闭区间[a,b]内所有的极值,以及f(a)和f(b),最大者为最大值,最小者为最小值.
●点击双基
1.若函数f(x)有导数,它的极值可在方程 (x)=0的根处来考查,求函数y=f(x)的极值方法如下:
(x)=0的根处来考查,求函数y=f(x)的极值方法如下:
(1)求导数 (x);
(x);
(2)求方程 (x)=0的根;
(x)=0的根;
(3)检查 (x)在方程
(x)在方程 (x)=0的根的左右的值的符号,如果左负右正,那么函数y=f(x)在这个根处取得极小值;如果左正右负,那么函数y=f(x)在这个根处取得极大值.
(x)=0的根的左右的值的符号,如果左负右正,那么函数y=f(x)在这个根处取得极小值;如果左正右负,那么函数y=f(x)在这个根处取得极大值.
13.3 导数的综合问题
●知识梳理
18、已知函数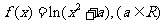
(1)求在函数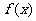 图象上点A
图象上点A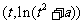 处的切线
处的切线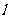 的方程;
的方程;
(2)若切线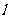 与y轴上的纵截距记为
与y轴上的纵截距记为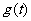 ,讨论
,讨论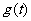 的单调增区间。
的单调增区间。
17、已知函数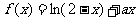 在
在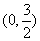 上是增函数,
上是增函数,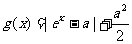 。当
。当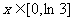 时,函数
时,函数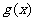 的最大值
的最大值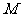 与
与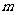 最小值的差为
最小值的差为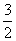 ,试求
,试求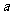 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com