
题目列表(包括答案和解析)
8. 设f(log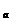 x)=
x)=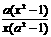 , ①.求f(x)的定义域; ②.在y=f(x)的图像上是否存在两个不同点,使经过这两点的直线与x轴平行?证明你的结论。 ③.求证:f(n)>n
(n>1且n∈N)
, ①.求f(x)的定义域; ②.在y=f(x)的图像上是否存在两个不同点,使经过这两点的直线与x轴平行?证明你的结论。 ③.求证:f(n)>n
(n>1且n∈N)
7. 已知数列{a }满足a
}满足a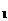 =1,a
=1,a =a
=a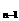 cosx+cos[(n-1)x], (x≠kπ,n≥2且n∈N)。
cosx+cos[(n-1)x], (x≠kπ,n≥2且n∈N)。
①.求a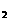 和a
和a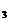 ; ②.猜测a
; ②.猜测a ,并用数学归纳法证明你的猜测。
,并用数学归纳法证明你的猜测。
6.
数列{a }的通项公式a
}的通项公式a =
=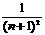 (n∈N),设f(n)=(1-a
(n∈N),设f(n)=(1-a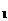 )(1-a
)(1-a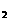 )…(1-a
)…(1-a ),试求f(1)、f(2)、f(3)的值,推测出f(n)的值,并用数学归纳法加以证明。
),试求f(1)、f(2)、f(3)的值,推测出f(n)的值,并用数学归纳法加以证明。
5. 用数学归纳法证明: |sinnx|≤n|sinx| (n∈N)。 (85年广东高考)
4. 用数学归纳法证明等式:cos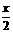 ·cos
·cos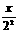 ·cos
·cos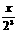 ·…·cos
·…·cos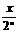 =
=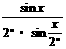 (81年全国高考)
(81年全国高考)
3. n∈N,试比较2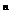 与(n+1)
与(n+1)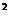 的大小,并用证明你的结论。
的大小,并用证明你的结论。
2. 用数学归纳法证明: 1×4+2×7+3×10+…+n(3n+1)=n(n+1)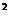 (n∈N)。
(n∈N)。
1. 用数学归纳法证明:6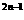 +1 (n∈N)能被7整除。
+1 (n∈N)能被7整除。
6. 设k棱柱有f(k)个对角面,则k+1棱柱对角面的个数为f(k+1)=f(k)+_________。
Ⅱ、示范性题组:
例1. 已知数列 ,得,…,
,得,…,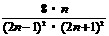 ,…。S
,…。S 为其前n项和,求S
为其前n项和,求S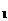 、S
、S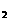 、S
、S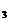 、S
、S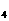 ,推测S
,推测S 公式,并用数学归纳法证明。 (93年全国理)
公式,并用数学归纳法证明。 (93年全国理)
[解]
计算得S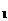 =
=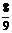 ,S
,S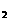 =
=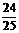 ,S
,S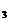 =
=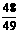 ,S
,S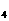 =
=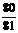 , 猜测S
, 猜测S =
=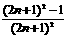 (n∈N)
(n∈N)
当n=1时,…
[注] 从试验、观察出发,用不完全归纳法作出归纳猜想,再用数学归纳法进行严格证明,这是探索性问题的证法,数列中经常用到。 (试值 → 猜想 → 证明)
[另解] 用裂项相消法求和:
例2. 设a =
=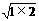 +
+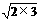 +…+
+…+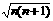 (n∈N),证明:
(n∈N),证明: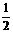 n(n+1)<a
n(n+1)<a <
<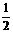 (n+1)
(n+1)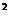 。
。
[解]
当n=1时,a =
=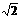 ,
,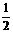 n(n+1)=
n(n+1)=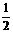 ,
,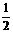 (n+1)
(n+1)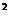 =2 , ∴ n=1时不等式成立。
=2 , ∴ n=1时不等式成立。
假设当n=k时不等式成立,即: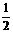 k(k+1)<a
k(k+1)<a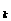 <
<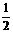 (k+1)
(k+1)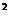 ,
,
当n=k+1时,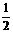 k(k+1)+
k(k+1)+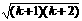 <a
<a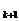 <
<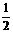 (k+1)
(k+1)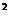 +
+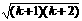
…
[注] 用数学归纳法解决与自然数有关的不等式问题,注意适当选用放缩法。
[另解]
也可采用放缩法直接证明。(抓住对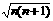 的分析,注意与目标比较)
的分析,注意与目标比较)
例3. 设数列{a }的前n项和为S
}的前n项和为S ,若对于所有的自然数n,都有S
,若对于所有的自然数n,都有S =
=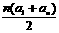 ,证明{a
,证明{a }是等差数列。 (94年全国文)
}是等差数列。 (94年全国文)
[分析]
要证等差数列,即证:a =a
=a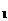 +(n-1)d
+(n-1)d
[解]
设a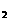 -a
-a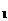 =d,猜测a
=d,猜测a =a
=a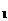 +(n-1)d
+(n-1)d
当n=1时,a =a
=a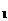 , ∴ 当n=1时猜测正确。
, ∴ 当n=1时猜测正确。
假设当n=k时,猜测正确,即:a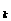 =a
=a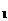 +(k-1)d ,
+(k-1)d ,
当n=k+1时,a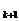 =S
=S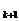 -S
-S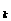 =
=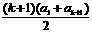 -
-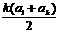 , 解得a
, 解得a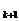 =…
=…
…
[注]
注意问题转化成数学式及a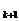 的得出。
的得出。
[另解]
可证a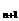 -a
-a = a
= a - a
- a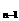 而得:
而得:
Ⅲ、巩固性题组:
5.
用数学归纳法证明3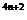 +5
+5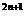 (n∈N)能被14整除,当n=k+1时对于式子3
(n∈N)能被14整除,当n=k+1时对于式子3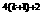 +5
+5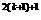 应变形为_______________________。
应变形为_______________________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com