
题目列表(包括答案和解析)
2.针对不同基础的学生,采取不同措施。对于基础薄弱的学生,由于基础差、意志力弱的问题,一方面鼓舞学生信心,开展励志教育,另一方面,勤于辅导,积极帮助,进行集中或个别辅导,尽力帮助学生解决问题。
1.要认真研究《考纲》,增强复习备考的针对性。针对《课标》和新《考纲》的对比研究。认真研究《课标》和新《考纲》,掌握对教学内容的要求层次和变化。特别是文科数学课程标准及考纲与以往相比出现了很大变化,在新的环境下,考什么内容和重要知识点怎样考要成为我们数学备课组经常研究的核心问题,把文理科考纲、今年的考纲与往年的考纲进行对比研究,弄清考纲的变化及要求,注意到对一些内容要求层次上的变化,如把“理解”或“掌握”降为“了解”;对考纲上没有的一些内容适当补充,如“分式不等式的解法”这一知识点,由于有很强的基础性和重要的应用价值,要及时补充。
6.对于函数模型及其应用,这是一块新增内容,课标:鼓励学生运用现代教育技术学习、探索和解决问题,例如:利用计算器、计算机画出指数函数、对数函数等的图象,探索、比较它们的变化规律,研究函数的性质,求方程的近似解等.课标还强调学生对过程的感受.大纲:强调建模解题,注重方法及结果.
①(07顺德一模)康成塑料制品厂今年1月、2月、3月生产某种产品分别为1万件,1.2万件、1.3万件,为估测作依据,用一个函数模拟该产品的月产量y和月份数x的关系,模拟函数可以选用二次函数y= ax2 + bx + c或函数 y= a•bx + c (其中a、b、c为常数,a≠0),已知4月份该产品的产量为1.37万件,问用上述哪个函数作为模拟函数好?请说明理由.
5.对于函数与方程,课标:对任一函数的零点进行研究,方法基本、简单,易于掌握;课标:求近似解可以无限精确.大纲:画图观察出方程的解的近似值如求方程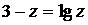 的近似解.
的近似解.
①(07山东)设函数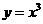 与
与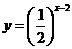 的图象的交点为
的图象的交点为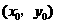 ,
,
则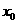 所在的区间是( )
所在的区间是( )
A.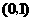 B.
B.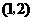 C.
C.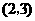 D.
D.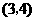
②(07广东)已知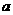 是实数,函数
是实数,函数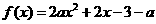 ,如果函数
,如果函数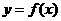 在区间
在区间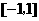 上有零点,求
上有零点,求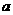 的取值范围.
的取值范围.
4.对于基本初等函数,课标要求学生了解无理指数幂,课标要求知道换底公式;课标对反函数不做要求,只提出知道指数函数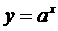 与对数函数
与对数函数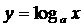 互为反函数(
互为反函数(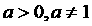 ).
).
①已知集合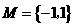 ,
,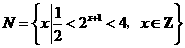 ,则
,则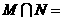 ( )
( )
A.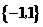 B.
B.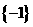 C.
C.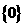 D.
D.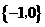
②(07山东)设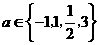 ,则使函数
,则使函数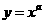 的定义域为
的定义域为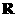 且为奇函数的所有
且为奇函数的所有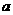 值为( )
值为( )
A.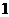 ,
,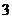 B.
B.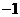 ,
,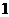 C.
C.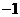 ,
,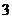 D.
D.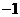 ,
,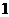 ,
,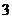
③(07广州二模)函数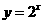 (
( )的反函数为
)的反函数为
A.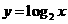 (
(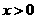 )
B.
)
B.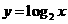 (
(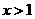 )
)
C.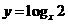 (
(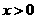 )
D.
)
D.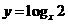 (
(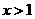 )
)
3.对于函数的性质,课标强化了用图象直观理解和研究函数的性质,强调了函数的实际应用;大纲侧重通过推理、证明研究函数的性质及应用。
①(07广州二模)下列函数中,既是偶函数又在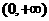 上单调递增的是
上单调递增的是
 A.
A. 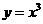 B
B 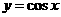 C
C 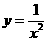 D
D
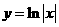
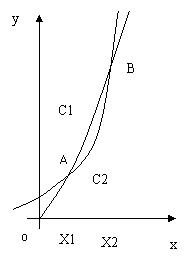
② (07广州二模)函数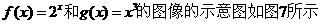
 设两函数的图像交于点
设两函数的图像交于点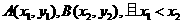
(1)请指出示意图中曲线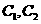 分别对应哪一个函数?
分别对应哪一个函数?
(2)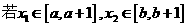 ,且
,且

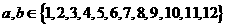 指出
指出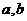 的值,并说明理由;
的值,并说明理由;
(3)结合函数图像示意图,判断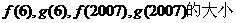
2.对于函数的概念,课标通过实例用变量的关系描述函数概念,比较生动、直观;而大纲是从抽象的对应关系来定义函数的概念;课标对求函数定义域和值域降低了要求;课标增加了“在实际情境中”,强调了函数的应用性;对分段函数的应用提出了具体的要求.
①(07广东)已知函数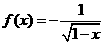 的定义域
的定义域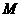 ,
,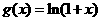 的定义域为
的定义域为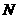 ,则
,则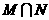 =( )
=( )
A.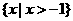 B.
B.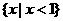 C.
C.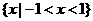 D.
D.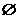
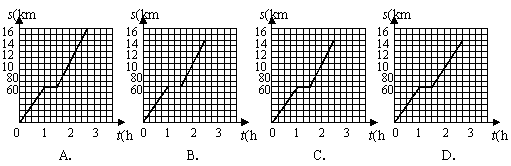
②(07广东)客车从甲地以60km/h的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80km/h的速度匀速行驶1小时到达内地.下列描述客车从甲地出发,经过乙地,最后到达丙地所经过的路程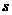 与时间
与时间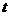 之间关系的图象中,正确的是( )
之间关系的图象中,正确的是( )
函数的主要内容有:集合的概念与运算,函数的概念及表示方法,函数的性质,基本初等函数(指数函数、对数函数、幂函数)、函数与方程,函数模型及其应用。课标与大纲相比,主要有以下变化:
1.对集合的概念,由理解变为了解,课标降低了要求; 课标正式提出了可以运用自然语言表示集合;课标对集合的包含、相等关系由了解变为理解。提高了要求;增加了“在具体情境中”,强调了集合的应用;课标对集合的并集、交集与补集运算提出了更具体的要求;课标强调了Venn图的应用.
①(07宁夏)设集合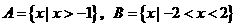 ,则
,则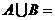 ( )
( )
A.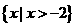 B.
B.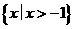
C.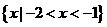 D.
D.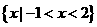
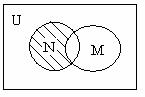 ②设全集
②设全集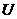 是实数集
是实数集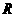 ,
,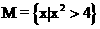 ,
,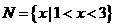 ,则图中阴影部分所表示的集合是( )
,则图中阴影部分所表示的集合是( )
A.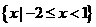 B.
B.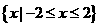
C.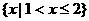 D.
D.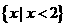
20.已知函数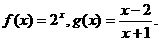
(1)证明:函数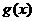 在
在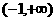 上为增函数;
上为增函数;
(2)用反证法证明方程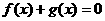 没有负数根.
没有负数根.
19、已知函数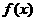 的图象与函数
的图象与函数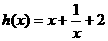 的图象关于点A(0,1)对称.
的图象关于点A(0,1)对称.
(Ⅰ)求函数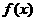 的解析式;
的解析式;
(Ⅱ)求函数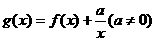 的单调区间.
的单调区间.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com