
题目列表(包括答案和解析)
7.正方体的八个顶点中,有四个顶点恰好是正四面体的顶点,则这个正方体的表面积与正四面体的表面积之比是 ( )
A.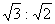 B.
B.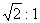 C.
C.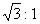 D.
D.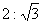
6.已知a>b>c>0,t是方程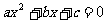 的实根,则t的取值范围是 ( )
的实根,则t的取值范围是 ( )
A.(-∞,-1) B.(-1,0) C.(0,1) D.(1,+∞)
4.已知向量a=(λ,-2),b=(-3,5),且a与b的夹角为钝角,则λ的取值范围是( )
A.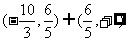 B.
B.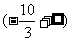
|
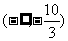 D.
D.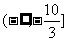
 5.如图,都不是正四面体的表面展开图的是 ( )
5.如图,都不是正四面体的表面展开图的是 ( )
A.①⑥ B.④⑤ C.②③ D.④⑥
3.若关于x的不等式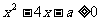 ,对任意
,对任意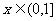 恒成立,则a的取值范围是( )
恒成立,则a的取值范围是( )
A. B.
B. C.
C.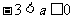 D.
D.
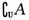 1.已知全集
1.已知全集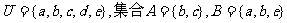 ,则( )∩B= ( )
,则( )∩B= ( )
A.{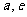 } B.
} B.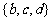 C.
C.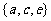 D.
D.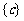
2.过点P(-2,4)作圆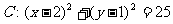 的切线l,直线
的切线l,直线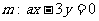 与直线l平行,则a的值是 ( )
与直线l平行,则a的值是 ( )
A.2 B.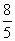 C.
C.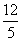 D.4
D.4
3。选修1-2第73页习题B组第2题、选修2-2第129页习题B组第2题
变式1:计算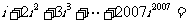 .
.

变式2:若 ,那么
,那么 的值是 .
的值是 .

选修1-2第73页习题A组选择第4题,选修2-2第129页习题A组选择第4题

变式1:. =( )
A. 2i B.-1+i C.1+i D.2
=( )
A. 2i B.-1+i C.1+i D.2
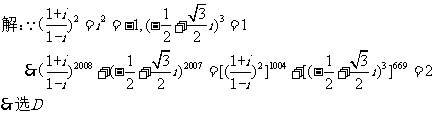
变式2:复数z= ,求1+z+z2的值;
,求1+z+z2的值;

2.选修1-2第65页习题A组第5题、选修2-2第119页A组习题第5题:
实数m取什么值时,复平面内表示复数 的点
的点
(1)位于第四象限? (2)位于第一、二象限?
(3)位于直线上
变式1:复数z=(a2-2a)+(a2-a-2)i对应的点在虚轴上,则(C)
A.a≠2或a≠1 B.a≠2且a≠1 C.a=2或a=0 D.a=0

变式2:已知复数 ,
, ,则在
,则在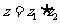 复平面上对应的点位于(
)
复平面上对应的点位于(
)
A.第一象限 B.第二象限 C.第三象限 D.第四象限
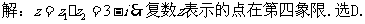
变式3:如果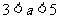 ,复数
,复数 在复平面上的
在复平面上的
对应点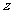 在 象限.
在 象限.

变式4:已知z0=2+2i,|z-z0|= ,
,
(1)求复数z在复平面内对应的点的轨迹
(2)求z为何值时,|z|有最小值,并求出|z|有最小值,
解(1)设z=x+yi(x,y∈R),由|z-z0|= ,
,
 即 |x+yi-(2+2i)|=|(x-2)+(y-2)i|=
即 |x+yi-(2+2i)|=|(x-2)+(y-2)i|= ,解得(x-2)2+(y-2)2=2
,解得(x-2)2+(y-2)2=2
∴复数z点的轨迹是以Z0(2,2)为圆心,
半径为 的圆。
的圆。
(2)当Z点在OZ 0的连线上时,|z|有最大值或最小值,
∵| OZ 0|=2 ,半径r=
,半径r= ,
,
∴当z=1+i时,|z|min=
1.选修1-2第62页例、选修2-2第116页例1:

变式1:若复数 是纯虚数,则
是纯虚数,则 = .
= .

变式2:使复数为实数的充分而不必要条件是 ( )
A. B.
B.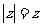 C.
C. 为实数
为实数  D.
D.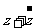 为实数
为实数
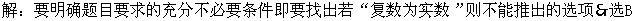 变式3:若有
变式3:若有 分别表示正实数集,负实数集,纯虚数集,则集合
分别表示正实数集,负实数集,纯虚数集,则集合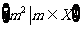 =( ).
=( ).
A. B.
B. C.
C.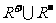 D.
D.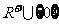
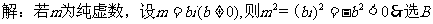
选修2-2第59页例1、例2
计算下列定积分:
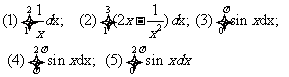
变式1:计算:;
(1)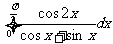 ;(2)
;(2)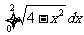
解:.(1)
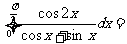
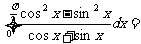
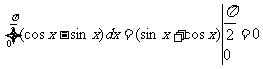
(2)利用导数的几何意义: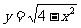 与x=0,x=2所围图形是以(0,0)为圆心,2为半径的四分之一个圆,其面积即为
与x=0,x=2所围图形是以(0,0)为圆心,2为半径的四分之一个圆,其面积即为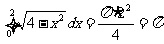 (图略)
(图略)
变式2: 求将抛物线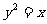 和直线
和直线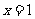 围成的图形绕
围成的图形绕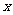 轴旋转一周得到的几何体的体积.
轴旋转一周得到的几何体的体积.
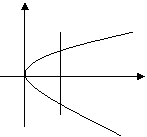 分析:利用定积分的定义解题,应当画出草图.
分析:利用定积分的定义解题,应当画出草图.
解:先求出抛物线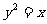 和直线
和直线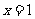 交点坐标(1,1),(1,-1)
交点坐标(1,1),(1,-1)
利用定积分的定义易得:
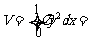
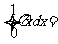
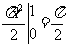
变式3:在曲线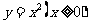 上某一点A处作一切线使之与曲线以及
上某一点A处作一切线使之与曲线以及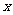 轴所围的面积为
轴所围的面积为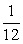 ,试求:(1)切点A的坐标;(2)在切点A的切线方程.
,试求:(1)切点A的坐标;(2)在切点A的切线方程.

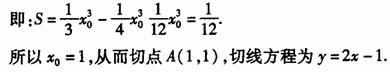
12.某厂生产某种产品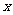 件的总成本
件的总成本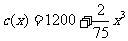 (万元),已知产品单价的平方与产品件数
(万元),已知产品单价的平方与产品件数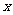 成反比,生产100件这样的产品单价为50万元,产量定为多少时总利润最大?
成反比,生产100件这样的产品单价为50万元,产量定为多少时总利润最大?
分析:先建立总利润的目标函数,总利润=总销售量-总成本C(x)= 产品件数*产品单价-C(x),因而应首先求出产品单价P(x)的解析式.
解:设产品的单价P元,据已知,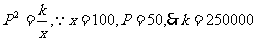 ,
,
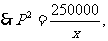
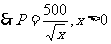 设利润为y万元,则
设利润为y万元,则
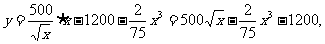
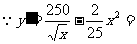
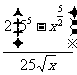 ,
,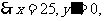
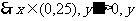 递增;
递增; 递减,
递减,
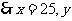 极大=
极大=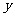 最大.
最大.
答:当产量为25万件时,总利润最大
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com