
题目列表(包括答案和解析)
11.曲线y=x3-3x上切线平行于x轴的交点的坐标是( )
A.(-1,2) B.(1,-2) C.(1,2) D.(-1,2)或(1,-2)
联想:(1)若函数f ( x )=ax3 + bx2 + cx + d(a>0)在R上为增函数,则
A.b2-3ac>0 B.b<0 , c>0 C.b=0 , c>0 D.b2-3ac<0
(2)已知函数f ( x )=x3 + ax2 + bx + c在x=-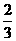 与x=1处都取得极值,若在[-1,2]时f ( x )< c2恒成立,则实数c的取值范围是
.
与x=1处都取得极值,若在[-1,2]时f ( x )< c2恒成立,则实数c的取值范围是
.
(3)函数f ( x )=ax3 + bx在x=1处有极值-2,点P是函数图象上任意一点,过P的切线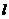 的倾斜角为α,则α的取值范围是
。
的倾斜角为α,则α的取值范围是
。
(4)抛物线C1:y=3x2和C2:y=-x2
+ 4tx交于原点O和点A,过点A作C2的切线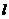 ,它与C1相交于点P,当t在实数范围内变化时,求线段AP的中点M的轨迹方程,并说明轨迹是什么图形?
,它与C1相交于点P,当t在实数范围内变化时,求线段AP的中点M的轨迹方程,并说明轨迹是什么图形?
10.已知函数f ( x )=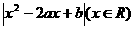 ,给出下列命题:①f ( x )必是偶函数;②f ( 0 )=
,给出下列命题:①f ( x )必是偶函数;②f ( 0 )=
f ( 2 )时f ( x )的图象必关于直线x=1对称;③若a2-b≤0则f ( x )在区间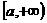 上是增函数;
上是增函数;
④f ( x )有最大值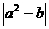 ,其中正确命题的序号是
。
,其中正确命题的序号是
。
联想:(1)设函数f ( x )=lg ( x2 +ax-a-1)给出下述命题:①f ( x )有最小值;②当a=0时,f ( x )的值域为R;③当a>0时,f ( x )在区间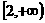 上有反函数;④若f ( x )在区间
上有反函数;④若f ( x )在区间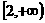 上单调递增,则实数a的取值范围是a≥-4,其中正确的命题是
。
上单调递增,则实数a的取值范围是a≥-4,其中正确的命题是
。
(2)定义在R上的偶函数f ( x ),且f ( x+1 )=- f ( x ),f ( x )在[0,1]上是增函数,关于f ( x )的判断:①f ( x )是周期函数;②f ( x )的图象关于直线x=1对称;③f ( x )在[-1,0]上是增函数;④f ( x )在[1,2]上是减函数;⑤f ( 0 )= f ( 2 ),则正确命题的序号是 。
9.椭圆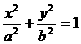 (a>b>0)的半焦距为c,若直线y=2x与椭圆一个交点的横坐标恰为
(a>b>0)的半焦距为c,若直线y=2x与椭圆一个交点的横坐标恰为
c,则椭圆的离心率为( )
A.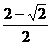 B.
B.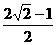 C.
C.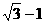 D.
D.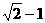
联想:(1)若椭圆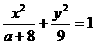 的离心率是
的离心率是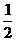 ,则实数a的值为
。
,则实数a的值为
。
(2)椭圆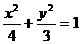 上有n个不同的点P1、P2、…、Pn,椭圆的右焦点为F,数列{
上有n个不同的点P1、P2、…、Pn,椭圆的右焦点为F,数列{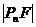 }是公差大于
}是公差大于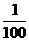 的等差数列,则n的最大值为
的等差数列,则n的最大值为
A.199 B.200 C.198 D.201
(3)若将离心率为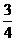 的椭圆
的椭圆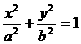 (a>b>0)绕着它的左焦点按逆时针方向旋转
(a>b>0)绕着它的左焦点按逆时针方向旋转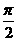 后,所得新椭圆的一条准线方程是3y+14=0,则新椭圆的另一条准线方程是( )
后,所得新椭圆的一条准线方程是3y+14=0,则新椭圆的另一条准线方程是( )
A.3y-14=0 B.3y-23=0 C.3y-32=0 D.3y-50=0
8.某厂生产电子元件,其产品的次品率为5%,现从一批产品中任意地连续取2件,其中次品数η的概率分布是
|
η |
0 |
1 |
2 |
|
P |
|
|
|
联想:(1)一个袋子里装有大小相同的3个红球和2个白球,从中同时取出2个球,则其中含有红球个数η的概率分布是
|
η |
0 |
1 |
2 |
|
P |
|
|
|
(2)四个纪念章A、B、C、D,投掷时正面向上的概率如下表所示,这四个纪念章同时投掷时,出现
|
纪念章 |
A |
B |
C |
D |
|
概 率 |
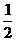 |
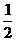 |
a |
a(0<a<1) |
n个正面的概率记作Pn。(Ⅰ)求概率Pi (i=0 , 1 , 2 , 3 , 4 )
(Ⅱ)求在概率Pi中P2为最大时,a的取值范围。
(3)5个身高均不相同的学生排成一排合影留念,高个子站在中间,从中间到左边一个比一个矮,从中间到右边也一个比一个矮,则这样的排法有 ( )
A.6种 B.8种 C.12种 D.16种
7.已知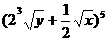 展开式的第三项为20,则y关于x的函数图象的大致形状为
。
展开式的第三项为20,则y关于x的函数图象的大致形状为
。
联想:(1)设f ( x )= ( x-1 )5 + 5 ( x -1 )4 + 10 ( x-1)3 + 10( x-1 )2 + 5x-4的图象关于直线y=x对称图象所对应的函数为g ( x ) ,则g ( x )的解析式为( )
A.x5
B.x C.x
C.x +1 D.(x-2)
+1 D.(x-2)
(2)已知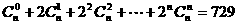 ,则
,则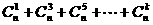 的值为(k是小于n的最大奇数)
的值为(k是小于n的最大奇数)
A.64 B.32 C.63 D.31
(3)( x2 + x-1)9 ( 2x +1 )4的展开式中,所有奇数次项的系数和为 .
6.函数y=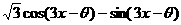 是奇函数,则θ等于(以下k
是奇函数,则θ等于(以下k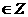 ) ( )
) ( )
A.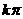 B.
B.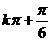 C.
C.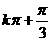 D.
D.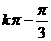
联想:(1)函数f ( x )=sin(wx+θ)cos (wx+θ) (w>0),以2为最小正周期,且能在x=2时取得最大值,则θ的一个值是( )
A.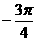 B.
B.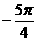 C.
C.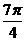 D.
D.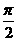
(2)为了使函数y=sinwx (w>0 )在区间[0,1]上至少出现50次最大值,则w的最小值是( )
A.98π
B.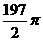 C.
C.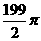 D.100π
D.100π
(3)设函数f ( x ) = sin ( wx+θ) ( w > 0 , 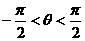 ),给出以下四个论断:
),给出以下四个论断:
①它的图象关于直线x=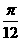 对称;②它的图象关于点(
对称;②它的图象关于点(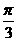 , 0)对称;
, 0)对称;
③它的周期为π;
④在区间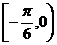 上是增函数;
上是增函数;
以其中两个论断作为条件,余下论断作为结论,写出你认为正确的两个正确命题:
5.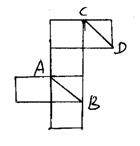 将正方体的纸盒展开(如图)直线AB、CD在原正
将正方体的纸盒展开(如图)直线AB、CD在原正
方体中的位置关系是( )
A.平行 B.垂直
C.相交且成600角 D.异面且成600角
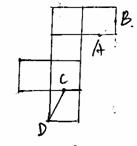
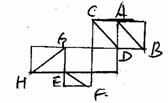
联想:(1)右图是一个正方体的表面展开图,A、B、C
均为棱的中点,D是顶点,则在正方体中,异面直线AB
和CD的夹角的余弦值为( )
A.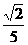 B.
B.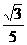
 C.
C.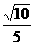 D.
D.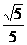
(2)右图表示一个正方体的展开图,图中AB、CD、
EF、GH这四条直线在原正方体中相互异面的有( )
A.2对 B.3对
C.4对 D.5对
4.设二次函数f ( x )对x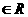 恒有f (1-x) = f
( 1+x ),且其图象开口向上,若
恒有f (1-x) = f
( 1+x ),且其图象开口向上,若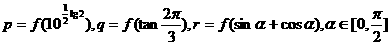 ,则p、q、r大小关系为( )
,则p、q、r大小关系为( )
A.p > q > r B.q > p > r C.q > r≥p D.q > p≥r
联想:(1)若x < y < 0,A=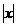 ,B=
,B=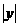 ,C=
,C=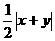 ,D=
,D=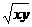 ,它们的关系是( )
,它们的关系是( )
A.B<D<C<A B.A<D<C<B C.A<C<D<B D.D<B<C<A
(2)α、β是锐角三角形的两个内角,x=sin(α+β),y=cosα+cosβ,z=sinα+sinβ,则x、y、z的大小关系是( )
A.x<y<z B.z<y<x C.x<z<y D.z<x<y
(3)△ABC中,三边a、b、c对角为A、B、C,且a>b>c,设p=sinAcosC,q=sinBcosB,r=sinCcosA,则p、q、r的大小为( )
A.p>q>r B.p>r>q C.r>p>q D.r>q>p
(4)已知函数f ( x )=log2(
x +1 )且a>b>c>0,则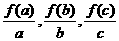 的大小为( )
的大小为( )
A.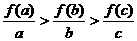 B.
B.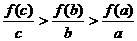
C.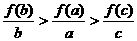 D.
D.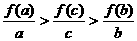
3.将圆( x-3 )2 +( y + 2)2=1按向量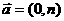 平移后,与直线y = x + 1相切,则n=( )
平移后,与直线y = x + 1相切,则n=( )
A.5 B.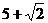 或
或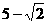 C.6 D.
C.6 D.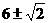
联想:(1)若函数y =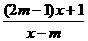 的图象按向量
的图象按向量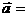 (5, -5)平移后得到的函数图象与原函数的反函数的图象重合,则实数m的值为( )
(5, -5)平移后得到的函数图象与原函数的反函数的图象重合,则实数m的值为( )
A.2 B.6 C.-6 D.不存在
(2)将函数y = cosx的图象按向量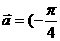 ,0)平移后,得到曲线C,又设曲线C与C′关于原点对称,则C′对应的函数解析式为
,0)平移后,得到曲线C,又设曲线C与C′关于原点对称,则C′对应的函数解析式为
(3)如果函数y=ax+b的反函数是它本身,那么点(a , b)的轨迹是( )
A.定点(1 , 0) B.定点(-1 , 0)
C.直线a=-1 D.直线a=-1和定点(1 , 0)
2.函数f ( x )= cos ( 3x +θ)的图象关于原点对称的充要条件是 ( )
A.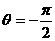 B.
B.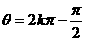 C.θ=kπ D.
C.θ=kπ D.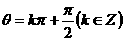
联想:(1)已知函数f ( x )=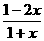 ,如果g ( x )的图象与函数y=f-1(x+1)的图象关于x-y=0对称,那么g(2)的值为( )
,如果g ( x )的图象与函数y=f-1(x+1)的图象关于x-y=0对称,那么g(2)的值为( )
A.-1 B.-2 C.-0.8 D.-0.2
(2)下列四个函数中,同时具有性质:①最小正周期为π;②图象关于直线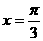 对称的函数是( )
对称的函数是( )
A.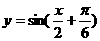 B.
B.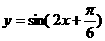
C.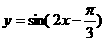 D.
D.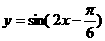
(3)函数y=sinx-cosx与函数y=sinx+cosx图象关于( )
A.x轴对称 B.y轴对称 C.直线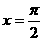 对称 D.直线
对称 D.直线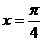 对称
对称
(4)函数y=sin2x + cos2x的图象关于直线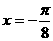 对称,则a=( )
对称,则a=( )
A.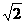 B.
B.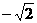 C.1
D.-1
C.1
D.-1
(5)已知x1是方程x+lgx=3的根,x2是x+10x=3的解,那么x1+x2等于( )
A.6 B.3 C.2 D.1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com