
题目列表(包括答案和解析)
5、已知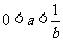 ,且
,且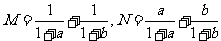 ,则
,则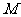 、
、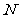 的大小关系是
的大小关系是
A. 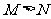 B.
B. 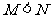 C.
C. 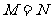 D. 不确定
D. 不确定
4、设函数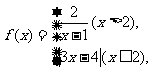 则使得
则使得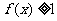 的自变量
的自变量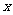 的取值范围为
的取值范围为
(A) (B)
(B)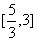 (C)
(C)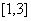 (D)
(D)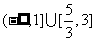
3、设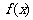 、
、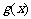 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当 ,
,
且 ,则不等式
,则不等式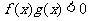 的解集是:
的解集是:
A.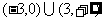 B.
B. C.
C. D.
D.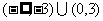
2、设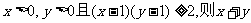 的取值范围是:
的取值范围是:
A.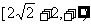 B.
B.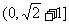 C.
C.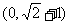 D.
D.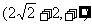
1、若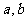 为实数,则“
为实数,则“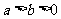 ”是“
”是“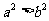 ”的:
”的:
A.充分不必要条件 B.必要不充条件
C.充要条件 D.既不充分也不必要条件
22.(本小题14分)
已知A、B、D三点不在一条直线上,且A(-2,0),B(2,0),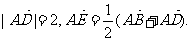
(1)求E点的轨迹方程;
(2)过A作直线交以A、B为焦点的随圆于M、N两点,线段MN的中点到y轴的距离为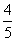 ,且直线MN与E点的轨迹相切,求椭圆的方程.
,且直线MN与E点的轨迹相切,求椭圆的方程.
21.(本题12分)
已知函数
(1)若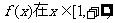 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;
(2)若x=3是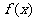 的极值点,求
的极值点,求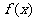 在
在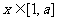 上的最小值和最大值.
上的最小值和最大值.
20.(本小题12分)
(理科答)A、B两队进行篮球决赛,共五局比赛,先胜三局者夺冠,且比赛结束。根据以往成绩,每场中A队胜的概率为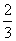 ,设各场比赛的胜负相互独立.
,设各场比赛的胜负相互独立.
(1)求A队夺冠的概率;
(2)设随机变量ξ表示比赛结束时的场数,求Eξ.
(文科答)甲、乙在罚球线投球命中的概率分别为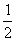 与
与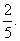
(1)甲、乙两人在罚球线各投球一次,求恰好命中一次的概率;
(2)甲、乙两人在罚球线各投球两次,求这四次投球中至少一次命中的概率.
19.(本小题12分)
如图,正三棱柱ABC-A1B1C1中,D、E分别是BC、CC1的中点,AB=AA1.
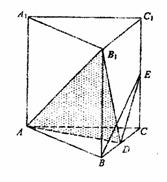 (1)求二面角B-AD-B1的正切值;
(1)求二面角B-AD-B1的正切值;
(2)证明:BE⊥平面AB1D;
(3)求异面直线DE与A1B1所成角的大小.
18.(本小题12分)
已知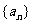 是等比数列,Sn是其前n项的和,a1,a7,a4成等差数列,求证:2S3,S6,S12-S6,成等比数列.
是等比数列,Sn是其前n项的和,a1,a7,a4成等差数列,求证:2S3,S6,S12-S6,成等比数列.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com