
题目列表(包括答案和解析)
2.等差数列的有关概念:
(1)等差数列的判断方法:定义法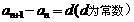 或
或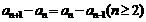 。
。
(2)等差中项:若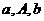 成等差数列,则A叫做
成等差数列,则A叫做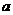 与
与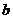 的等差中项,且
的等差中项,且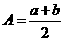 。
。
1、数列的概念:数列是一个定义域为正整数集N*(或它的有限子集{1,2,3,…,n})的特殊函数,数列的通项公式也就是相应函数的解析式。
4.等比差数列
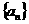 :
: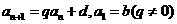 的通项公式为
的通项公式为
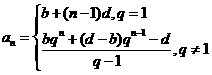 ;
;
其前n项和公式为
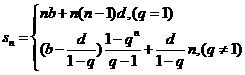 .
.
3.等比数列的通项公式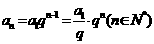 ;
;
其前n项的和公式为
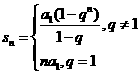 或
或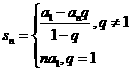 .
.
2.等差数列的通项公式
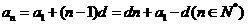 ;
;
其前n项和公式为
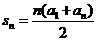
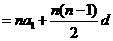
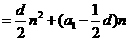 .
.
1.数列的同项公式与前n项的和的关系
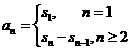 ( 数列
( 数列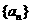 的前n项的和为
的前n项的和为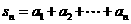 ).
).
8、平面直角坐标系中,O为坐标原点,给定两点A(1,0)、B(0,-2),点C满足 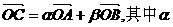 、
、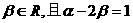
(1)求点C的轨迹方程;
(2)设点C的轨迹与椭圆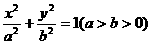 交于两点M、N,且以MN为直径的圆过原点,求证:
交于两点M、N,且以MN为直径的圆过原点,求证: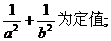
(3)在(2)的条件下,若椭圆的离心率不大于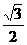 ,求椭圆实轴长的取值范围.
,求椭圆实轴长的取值范围.
解:(1)设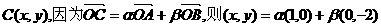
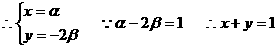
即点C的轨迹方程为x+y=1 。
(2)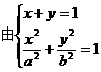 得:(a2+b2)x2-2a2x+
a2- a2b2=0
得:(a2+b2)x2-2a2x+
a2- a2b2=0
设M(x1,y1),N(x2,y2),则“
x1+ x2=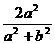 , x1x2=
, x1x2=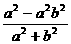
因为以MN为直径的圆过原点为,
所以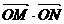 =0,即x1x2+y1y2=0
=0,即x1x2+y1y2=0
∴x1x2+(1-x1)(1-x2)=1-(x1+
x2)+2 x1x2=1-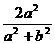 +2
+2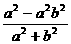 =0
=0
即a2+b2-2 a2b2=0
∴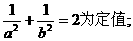
(3)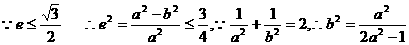
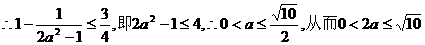
∴椭圆实轴长的取值范围是(0,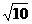
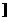 。
。
7、已知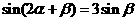 ,设
,设 ,记
,记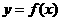
(1)求证:tan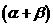 =2tan
=2tan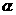
(2)求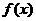 的表达式;
的表达式;
(3)定义正数数列{an};a1=2,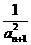 =2
=2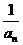
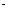
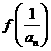 (n
(n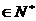 )。
)。
试求数列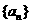 的通项公式。
的通项公式。
解:(1)由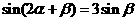 ,得sin
,得sin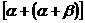 =3sin
=3sin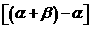 ,即
,即
sin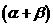 cos
cos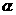 =2cos
=2cos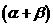 sin
sin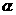
故tan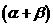 =2tan
=2tan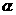
(2)由tan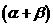 =2tan
=2tan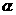 得
得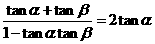 即
即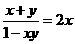 。解得
。解得
y=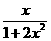 故
故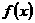 =
=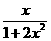
(3)因为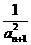 =2
=2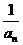
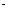
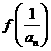 =2
=2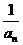
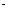
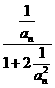 ,
,
所以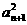 =
=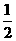
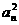 +1即
+1即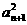 -2=
-2=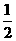 (
(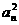 -2)
-2)
因此{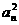 -2}是首项为2,公比为
-2}是首项为2,公比为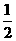 的等比数列。
的等比数列。
所以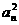 -2=2
-2=2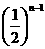 故an=
故an=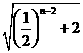 。
。
6、在十进制中,若一个至少有两位数字的正整数除了最左边的数字外,其余各个数字都小于其左边的数字时,则称它为递降正整数.所有这样的递降正整数的个数为(D )
(A)1001 (B)1010 (C)1011 (D)1013
解:当正整数为两位数时,有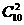 个
个
当正整数为三位数时,有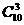 个
个
………
当正整数为十位数时,有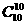 个
个
由分类计数原理得共有正整数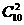 +
+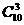 +…+
+…+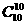 =210-
=210-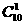 -
-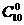 =1013
=1013
故选D。
5、在直角坐标系xOy中,已知点A(0,1)和点B(-3,4),C点在AB上且OC是∠AOB的角平分线,则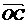 = (-
= (-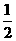 ,
,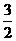 ) 。
) 。
解:由题设知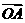 =(0,1),
=(0,1),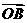 =(-3,4)
=(-3,4)
 OC是∠AOB的角平分线
OC是∠AOB的角平分线
 可设
可设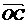 =
=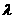 (
(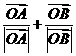 )=
)=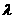
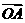 +
+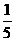
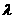
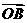
又C点在AB上
所以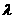 +
+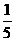
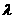 =1解得
=1解得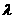 =
=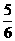
故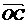 =
=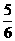
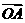 +
+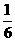
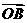 =(-
=(-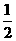 ,
,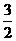 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com