
题目列表(包括答案和解析)
20.(本小题满分14分)过抛物线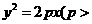

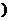 的对称轴上的定点
的对称轴上的定点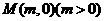 ,作直线
,作直线 与抛物线相交于
与抛物线相交于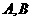 两点.
两点.
(1)试证明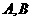 两点的纵坐标之积为定值;
两点的纵坐标之积为定值;
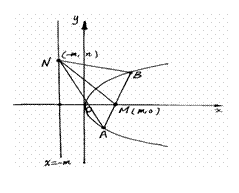 (2)若点
(2)若点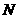 是定直线
是定直线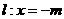 上的任一点,试探索三条直线
上的任一点,试探索三条直线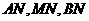 的斜率之间的关系,并给出证明.
的斜率之间的关系,并给出证明.
19.(本小题满分14分,第一、第二小问满分各6分)
如图,在斜三棱柱ABC-A1B1C1 中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成600的角, AA1= 2.底面ABC是边长为2的正三角形,其重心为G点。E是线段BC1上一点,且BE=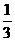 BC1 .
BC1 .
(1)求证: GE∥侧面AA1B1B ;
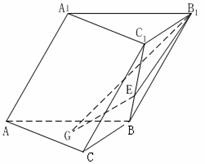 (2)求平面B1GE与底面ABC所成锐二面角的大小 .
(2)求平面B1GE与底面ABC所成锐二面角的大小 .
18.(本小题满分14分)已知函数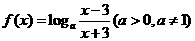 .
.
(1)求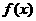 的定义域,并判断
的定义域,并判断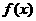 的奇偶性;
的奇偶性;
(2)解关于 的不等式:
的不等式: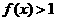 ;
;
17.(本小题满分12)已知向量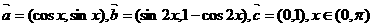 .
.
(1)向量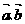 是否共线?证明你的结论;
是否共线?证明你的结论;
(2)若函数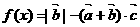 ,求
,求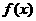 的最小值,并指出取得最小值时的
的最小值,并指出取得最小值时的 值.
值.
16.等比数列 的公比为
的公比为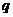 ,其前
,其前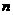 项的积为
项的积为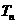 ,并且满足条件
,并且满足条件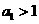 ,
, ,
,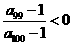 。给出下列结论:①
。给出下列结论:①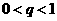 ;②
;②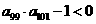 ③
③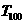 的值是
的值是 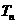 中最大的;④使
中最大的;④使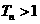 成立的最大自然数
成立的最大自然数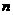 等于198。其中正确的结论是
.
等于198。其中正确的结论是
.
15.在△ABC中,角A,B,C所对的边分别是a,b,c,且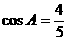 ,
,  ,△ABC的面积
,△ABC的面积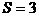 ,则a = .
,则a = .
14. 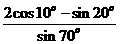 的值等于
.
的值等于
.
13.定义一种运算“ ”对于正整数满足以下运算性质:
”对于正整数满足以下运算性质:
(1) ;(2)
;(2)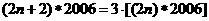 ,则
,则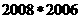 的值是
的值是
11命题“若 都是偶数,则
都是偶数,则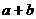 是偶数”的否命题是_________
是偶数”的否命题是_________
12. 以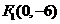 、
、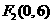 为焦点且过点
为焦点且过点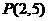 的双曲线的标准方程为
.
的双曲线的标准方程为
.
10.半径为4的球面上有A、B、C、D四点,且AB,AC,AD两两互相垂直,则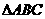 、
、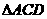 、
、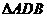 面积之和
面积之和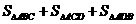 的最大值为 ( )
的最大值为 ( )
A.8 B.16 C.32 D.64
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com