
题目列表(包括答案和解析)
(二)直线方程
1. 直线方程的五种形式及适用范围
(1)斜截式: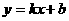 不含与
不含与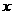 轴垂直的直线
轴垂直的直线
(2)点斜式: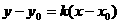 不含与
不含与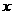 轴垂直的直线
轴垂直的直线
(3)两点式: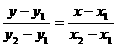 不含与
不含与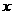 轴、
轴、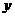 轴垂直的直线
轴垂直的直线
(4)截矩式: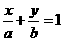 不含过原点和与
不含过原点和与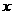 轴、
轴、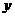 轴垂直的直线
轴垂直的直线
(5)一般式: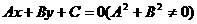 无限制(可表示任何直线)
无限制(可表示任何直线)
注:两点式的“改良”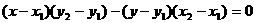 可表示任何直线。
可表示任何直线。
2. 直线系:
(1)平行直线系: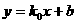 (
(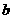 为待定系数,斜率
为待定系数,斜率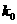 已知)
已知)
(2)过定点直线系: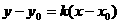 (
(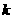 为待定系数,点
为待定系数,点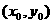 为已知)
为已知)
(3)过两直线交点的直线系:已知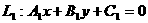 ;
;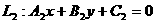 ,则
,则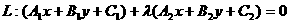 (
(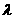 为参数--待定系数)
为参数--待定系数)
L是过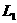 与
与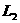 交点的直线系 (不含
交点的直线系 (不含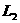 )
)
若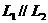 ,则L是与
,则L是与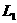 与
与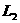 平行的直线系。
平行的直线系。
注:(1)与已知直线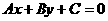 平行的直线系:
平行的直线系: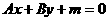 (
( 为参数)
为参数)
(2)与已知直线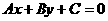 垂直的直线系:
垂直的直线系: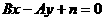 (
(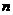 为参数)
为参数)
(一)直线的倾斜角(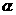 )和斜率(
)和斜率(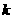 )
)
1. 定义 倾斜角范围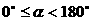 斜率:
斜率: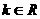
2. 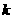 与
与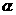 的关系:
的关系: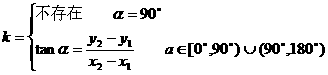

注:准确地把握这两个概念,关注斜率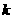 不存在带来的问题。
不存在带来的问题。
[例] (1)直线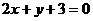 的斜率
的斜率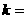 ,倾斜角
,倾斜角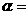 。
。
(2)若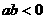 ,则直线
,则直线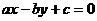 的斜率 ,倾斜角 。
的斜率 ,倾斜角 。
拓展:取消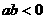 的限制,结论如何。
的限制,结论如何。
(3)直线L过点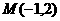 且与以
且与以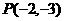 ,
,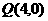 为端点的线段PQ相交,则斜率的取值范围 ,倾斜角的取值范围 。
为端点的线段PQ相交,则斜率的取值范围 ,倾斜角的取值范围 。
(4)若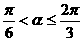 ,则
,则 。
。
(5)若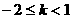 时,则
时,则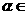 。
。
答案:(1)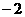 ;
; (2)
(2)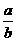 ;
;
(3)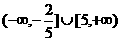 ;
;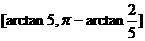
(4)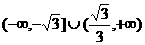 (5)
(5)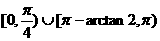
直线
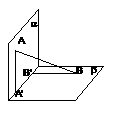
9..(全国II)如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α、β所成的角分别为和,过A、B分别作两平面交线的垂线,垂足为A′、B′,则AB∶A′B′=
(A)2∶1 (B)3∶1 (C)3∶2 (D)4∶3
解析:连接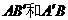 ,设AB=a,可得AB与平面
,设AB=a,可得AB与平面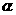 所成的角为
所成的角为

 ,在
,在 ,同理可得AB与平面
,同理可得AB与平面 所成的角为
所成的角为 ,所以
,所以 ,因此在
,因此在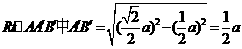 ,所以
,所以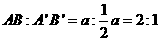 ,故选A
,故选A
[典型考例]
例1.(P75例3) 如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面CDE是等边三角形,棱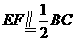
 (I)证明
(I)证明 平面
平面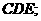 (II)设
(II)设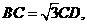 证明
证明 平面
平面
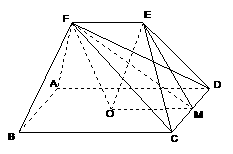 (19)本小题考查直线与平面平行、直线与平面垂直等基础知识,考查空间想象能力和推理论证能力。满分12分。
(19)本小题考查直线与平面平行、直线与平面垂直等基础知识,考查空间想象能力和推理论证能力。满分12分。
(I)证明:取CD中点M,连结OM。
在矩形ABCD中,
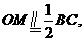 又
又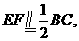
则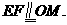 连结EM,于是
连结EM,于是
四边形EFOM为平行四边形。

又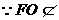 平面CDE,且
平面CDE,且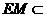 平面CDE,
平面CDE,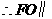 平面CDE。
平面CDE。
(II)证明:连结FM。由(I)和已知条件,在等边 中,
中,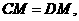
 且
且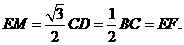
因此平行四边形EFOM为菱形,从而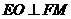 。
。
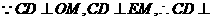 平面EOM,从而
平面EOM,从而
而 所以
所以 平面
平面
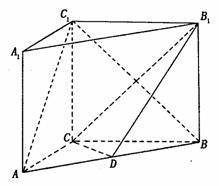 例2. 如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=4,AB=5点D是AB的中点, (I)求证:AC⊥BC1; (II)求证:AC 1//平面CDB1; (III)设BD1的中点为F,求三棱锥B1-BEF的体积
例2. 如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=4,AB=5点D是AB的中点, (I)求证:AC⊥BC1; (II)求证:AC 1//平面CDB1; (III)设BD1的中点为F,求三棱锥B1-BEF的体积
证:(I)直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4AB=5,
∴ AC⊥BC,且BC1在平面ABC内的射影为BC,∴ AC⊥BC1;
(II)设CB1与C1B的交点为E,连结DE,∵ D是AB的中点,E是BC1的中点,∴ DE//AC1,
∵ DE 平面CDB1,AC1
平面CDB1,AC1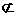 平面CDB1,∴ AC1//平面CDB1;
平面CDB1,∴ AC1//平面CDB1;
例2.已知ABCD是上.下底边长分别为2和6,高为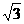 的等腰梯形,将它沿对称轴OO1折成直二面角
的等腰梯形,将它沿对称轴OO1折成直二面角
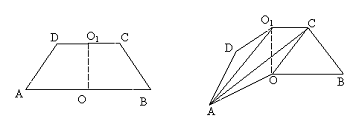 (Ⅰ)证明:AC⊥BO1;
(Ⅰ)证明:AC⊥BO1;
(Ⅱ)求点O1到平面AOC的距离。
(III)求四面体O1-ACO的体积。
(I)证明 由题设知OA⊥OO1,OB⊥OO1.
所以∠AOB是所折成的直二面角的平面角,
即OA⊥OB. 故可以O为原点,OA、OB、OO1
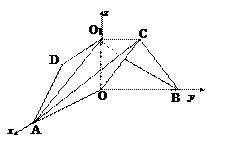 所在直线分别为
所在直线分别为 轴、y轴、z轴建立空间直角坐标系,
轴、y轴、z轴建立空间直角坐标系,
如图3,则相关各点的坐标是A(3,0,0),
B(0,3,0),C(0,1,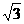 )O1(0,0,
)O1(0,0,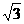 ).
).
从而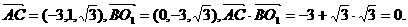
所以AC⊥BO1.
例3.如图,在底面为平行四边形的四棱锥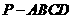 中,
中, ,
,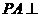 平面
平面 ,且
,且 ,点
,点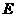 是
是 的中点.(Ⅰ)求证:
的中点.(Ⅰ)求证: ;(Ⅱ)求证:
;(Ⅱ)求证: 平面
平面 ;
;
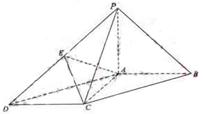 (Ⅲ)求四面体B-AED的体积。
(Ⅲ)求四面体B-AED的体积。
解:(1)由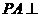 平面
平面 可得PA^AC
可得PA^AC
又 ,所以AC^平面PAB,所以
,所以AC^平面PAB,所以

(2)如图,连BD交AC于点O,连EO,则
EO是△PDB的中位线,\EO PB
PB
\PB 平面
平面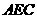
(3)如图,取AD的中点F,连EF,FO,则EF是△PAD的中位线,\EF PA又
PA又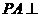 平面
平面 ,\EF^平面
,\EF^平面
同理FO是△ADC的中位线,\FO AB\FO^AC由三垂线定理可知\ÐEOF是二面角E-AC-D的平面角.又FO=
AB\FO^AC由三垂线定理可知\ÐEOF是二面角E-AC-D的平面角.又FO=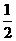 AB=
AB=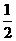 PA=EF\ÐEOF=45°而二面角
PA=EF\ÐEOF=45°而二面角 与二面角E-AC-D互补,故所求二面角
与二面角E-AC-D互补,故所求二面角 的大小为135°.
的大小为135°.
 例4.如图,已知正三棱柱ABC-A1B1C1的侧棱长和底面边长均为1,M是底面BC边上的中点,N是侧棱CC1上的点。(Ⅰ)当B1M⊥AN时,求CN的长度;(Ⅱ)若CN=
例4.如图,已知正三棱柱ABC-A1B1C1的侧棱长和底面边长均为1,M是底面BC边上的中点,N是侧棱CC1上的点。(Ⅰ)当B1M⊥AN时,求CN的长度;(Ⅱ)若CN=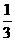 时,求点B1到平面AMN的距离。
时,求点B1到平面AMN的距离。
8.已知a、b、c是直线, 是平面,给出下列命题:①若
是平面,给出下列命题:①若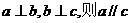 ②若
②若
 ③若
③若 ;④若a与b异面,且
;④若a与b异面,且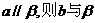 相交; ⑤若a与b异面,则至多有一条直线与a,b都垂直. 其中真命题的个数是 ( ) A.1子 B.2 C.3 D.4
相交; ⑤若a与b异面,则至多有一条直线与a,b都垂直. 其中真命题的个数是 ( ) A.1子 B.2 C.3 D.4
7.给出下列关于互不相同的直线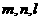 和平面
和平面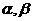 的四个命题:
的四个命题:
③
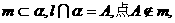 则
则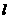 与m不共面;
与m不共面;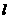 、m是异面直线,
、m是异面直线,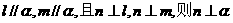 ;
;
④
若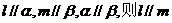 ;若
;若 ,则
,则
其中为假命题的是 (C)(A)① (B)② (C)③ (D)④
5.(上海卷)如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是 .
解:正方体中,一个面有四条棱与之垂直,六个面,共构成24个“正交线面对”;而正方体的六个对角截面中,每个对角面又有两条面对角线与之垂直,共构成12个“正交线面对”,所以共有36个“正交线面对”;6. 在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的是(C)
(A)BC//平面PDF (B)DF⊥平面PA E
(C)平面PDF⊥平面ABC (D)平面PAE⊥平面 ABC
4.(上海卷)若空间中有四个点,则“这四个点中有三点在同一直线上”是“这四个点在同一平面上”的 ( )
(A)充分非必要条件;(B)必要非充分条件;(C)充要条件;(D)非充分非必要条件
解:充分性成立: “这四个点中有三点在同一直线上”有两种情况:1)第四点在共线三点所在的直线上,可推出“这四个点在同一平面上”;2)第四点不在共线三点所在的直线上,可推出“这四点在唯一的一个平面内”;必要性不成立:“四个点在同一平面上”可能推出“两点分别在两条相交或平行直线上”; 故选(A)
2.(北京卷)平面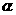 的斜线
的斜线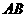 交
交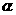 于点
于点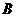 ,过定点
,过定点 的动直线
的动直线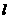 与
与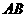 垂直,且交
垂直,且交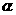 于点
于点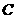 ,则动点
,则动点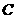 的轨迹是
的轨迹是
(A)一条直线 (B)一个圆(C)一个椭圆 (D)双曲线的一支
1.已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面.给出下列的四个命题: ①若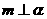 ,
,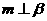 ,则
,则 ;②若
;②若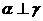 ,
,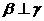 ,则
,则 ;③若
;③若 ,
,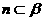 ,
,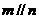 ,则
,则 ;
;
④若m、n是异面直线, ,
,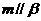 ,
,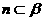 ,
, ,则
,则 ,其中真命题是
,其中真命题是
A.①和② B.①和③ C.③和④ D.①和④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com