
题目列表(包括答案和解析)
8、已知向量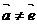 ,
,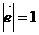 满足:
满足: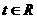 ,恒有
,恒有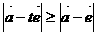 ,则
,则
A、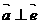 B、
B、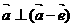
C、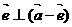 D、
D、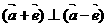
7、有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点。已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是
A、4 B、5 C、6 D、7
6、点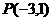 在椭圆
在椭圆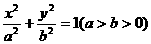 的左准线上,过点
的左准线上,过点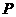 且方向为
且方向为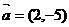 的光线,经直线
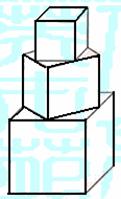
的光线,经直线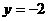 反射后通过椭圆的左焦点 ,则这个椭圆的离心率为
反射后通过椭圆的左焦点 ,则这个椭圆的离心率为
 A、
A、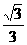 B、
B、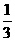 C、
C、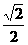 D、
D、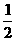
5、以平行六面体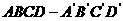 的任意三个顶点为顶点作三角形,从中随机取出两个三角形,则这两个三角形不共面的概率
的任意三个顶点为顶点作三角形,从中随机取出两个三角形,则这两个三角形不共面的概率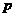 为
为
A、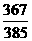 B、
B、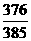 C、
C、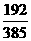 D、
D、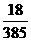
4、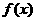 是定义在
是定义在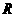 上的以3为周期的奇函数,且
上的以3为周期的奇函数,且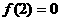 ,则方程
,则方程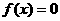 在
在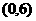 内解的个数的最小值是
内解的个数的最小值是
A、2 B、3 C、4 D、5
3、点 是
是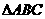 所在平面内一点,满足
所在平面内一点,满足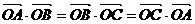 ,则点
,则点 是
是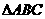 的
的
A、三个内角的角平分线的交点
B、三条边垂直平分线的交点
C、三条中线的交点
D、三条高的交点
2、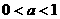 ,下列不等式一定成立的是
,下列不等式一定成立的是
A、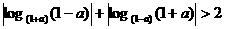
B、
C、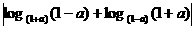

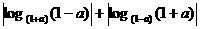
D、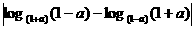

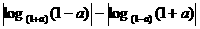
[例8]已知函数y=f (x)(x∈D),若对于任意的x1∈D,当f (x1)≠C时,存在唯一的x2∈D,且x1≠x2,使 = C(C为常数),则称函数y=f (x)在D上的均值为C。试写出一个均值为0的函数 .
[分析]f (x1)+ f (x2) = 0,联想点的对称性,且特殊化奇函数f (x)≠0均可。
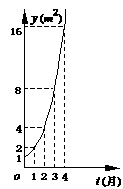
『类题1』 如图所示的是某池塘中的浮萍蔓延的面积y(m2)与时间t(月)的关系:y=a t,有以下叙述:(1)这个指数函数的底数为2;(2)第5个月时,浮萍面积就会超过30 m2;(3)浮萍从4 m2蔓延到12 m2需要经过1.5个月;(4)浮萍每月增加的面积都相等;(5)若浮萍蔓延到2 m2、3 m2、6 m2所经过的时间分别是t1、t2、t3,则t1+ t2= t3;其中正确的是( )
A.(1)(2) B.(1)(2)(3)(4)
C.(2)(3)(4)(5) D.(1)(2)(5)
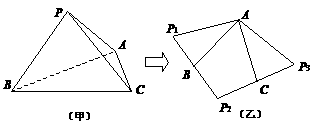 『类题2』
将三棱锥P-ABC(如图甲),沿三条侧棱剪开后,展开成如图乙的形状,其中P1、B、P2共线,P2、C、P3共线,且P1P2 = P2P3,则在三棱锥P-ABC中,PA与BC所成的角是( )
『类题2』
将三棱锥P-ABC(如图甲),沿三条侧棱剪开后,展开成如图乙的形状,其中P1、B、P2共线,P2、C、P3共线,且P1P2 = P2P3,则在三棱锥P-ABC中,PA与BC所成的角是( )
 A.30° B.45°
A.30° B.45°
C.60° D.90°
『类题3』 已知四个面都是直角三角形的三棱锥,其中三个面展开后构成一个直角梯形ABCD,如图AD⊥AB,AD⊥DC,AB=1,BC=,CD=2,则这个三棱锥的外接球的表面积是 (结果可含π)
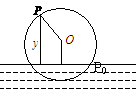 『类题4』如图是一个直径为8米的水轮,水轮圆心距水面2米,已知水轮每分钟转动4圈,水轮上的点P相对于水面的高度y(米)与时间x(秒)满足函数关系y = Asin(ωx+φ)+h (x=0时,P点位于P0处),则有
①A=4; ②
『类题4』如图是一个直径为8米的水轮,水轮圆心距水面2米,已知水轮每分钟转动4圈,水轮上的点P相对于水面的高度y(米)与时间x(秒)满足函数关系y = Asin(ωx+φ)+h (x=0时,P点位于P0处),则有
①A=4; ②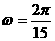 ;③
;③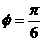 ; ④h=2 .其中所有正确结论的序号为
; ④h=2 .其中所有正确结论的序号为
『类题5』在平面几何里,有勾股定理:“设△ABC的两边AB、AC互相垂直,则AB2+AC2=BC2”,拓展到空间,类比平面几何定理,研究三棱锥的侧面面积与底面面积的关系,可以得出正确的结论是:“设三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,则 .”(S△ABC 2+ S△ACD 2+ S△ADB 2= S△BCD 2)
『类题6』某班有男、女生各20人,在一次数学测验中,男生的成绩统计分析得均分为95,标准差为6;女生成绩统计分析得均分为85,标准差为4.则全班统计分析得均分和标准差分别为
.(90;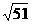 )
)
『类题7』在某次乒乓球单打比赛中,原计划每两名选手恰好比赛一场,但有3名选手各自比赛了2场就退了下来,这样,全部比赛只进行了50场,那么上述3名选手之间比赛的场数是 ( B )
A.0 B.1 C.2 D.3
『类题8』:(上海卷16、2004年第16题)某地2004年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下:
|
行业名称 |
计算机 |
机械 |
营销 |
物流 |
贸易 |
|
应聘人数 |
215830 |
200250 |
154676 |
74570 |
65280 |
|
行业名称 |
计算机 |
营销 |
机械 |
建筑 |
化工 |
|
招聘人数 |
124620 |
102935 |
89115 |
76516 |
70436 |
若用同一行业应聘人数与招聘人数比值的大小来衡量该行业就业情况,则根据表中数据,就业形势一定是( B )
A.计算机行业好于化工行业 B.建筑行业好于物流行业
C.机械行业最紧张 D.营销行业比贸易行业紧张
练习
1、函数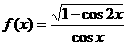
A、在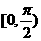 ,
,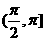 上递增,在
上递增,在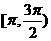 ,
,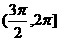 上递减
上递减
B、在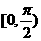 ,
,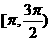 上递增,在
上递增,在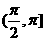 ,
,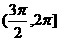 上递减
上递减
C、在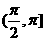 ,
,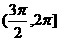 上递增,在
上递增,在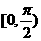 ,
,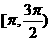 上递减
上递减
D、在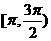 ,
,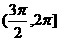 上递增,在
上递增,在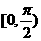 ,
,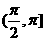 上递减
上递减
[例5]设函数 f(x)=x3+ax2+2bx+c.若当 x∈(0,1)时,f(x)取得极大值;x∈(1,2)时,f(x)取得极小值,则 的取值范围是 .
 提示:f´(x)= x2+ax+2b,令f´(x)=0,由条件知,上述方程应满足:一根在(0,1)之间,另一根在(1,2)之间,∴ ,得 ,在aob坐标系中,作出上述区域如图所示,而
的几何意义是过两点P(a,b)与A(1,2)的直线斜率,而P(a,b)在区域内,由图易知kPA∈(,1).
提示:f´(x)= x2+ax+2b,令f´(x)=0,由条件知,上述方程应满足:一根在(0,1)之间,另一根在(1,2)之间,∴ ,得 ,在aob坐标系中,作出上述区域如图所示,而
的几何意义是过两点P(a,b)与A(1,2)的直线斜率,而P(a,b)在区域内,由图易知kPA∈(,1).
『类题1』α是△ABC的内角,若sinα+cosα=- ,则tanα的值是( )
A.- B.- C. D.
方程思想:
[方法1] = -(+ cosα)
(>0)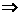 1 - cos2α=(+ cosα)2
1 - cos2α=(+ cosα)2
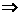 cosα= - (舍正),sinα= ,tanα=-
;
cosα= - (舍正),sinα= ,tanα=-
;
[方法2](sinα+cosα)2 = 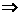 sinαcosα=
- ,构造方程 x2 + x- = 0
sinαcosα=
- ,构造方程 x2 + x- = 0
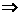 sinα= ,cosα=
- ;
sinα= ,cosα=
- ;
[方法3]令tan = t,则 + = - (万能公式),解得t =3 (舍负),
tanα= = - ;
函数思想:
[方法4]sinα+cosα= -
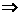 <α<π,又y = tanα增
<α<π,又y = tanα增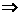 -1<tanα<0,故选B;
-1<tanα<0,故选B;
[方法5] 已知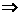 sinα= -(+ cosα)
sinα= -(+ cosα)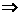 tanα= -(1 +
)
tanα= -(1 +
)
且 -1<cosα< -  - < tanα<0 ,选B;
- < tanα<0 ,选B;
数形结合思想:
 [方法6]构造如图的三角形,对照题设知sinα= ,cosα=
- ;
[方法6]构造如图的三角形,对照题设知sinα= ,cosα=
- ;
[方法7]观察研究 sinα+cosα= - 知0< sinα<- cosα<1,
只能选B。
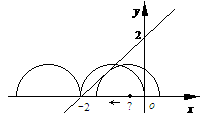 『类题2』设P是曲线 y=x3-x+上任意一点,点P处切线的倾斜角为α,则α的取值范围是
.[0,)∪[,π)
『类题2』设P是曲线 y=x3-x+上任意一点,点P处切线的倾斜角为α,则α的取值范围是
.[0,)∪[,π)
『类题3』 若曲线y = 与y = x+2有且仅有一个公共点P,O为坐标原点,则|OP|2的取值范围是 . 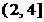
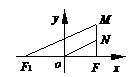 『类题4』已知双曲线
上一点M到右焦点F的距离为11,N是MF的中点,O为坐标原点,则|ON|等于( )
『类题4』已知双曲线
上一点M到右焦点F的距离为11,N是MF的中点,O为坐标原点,则|ON|等于( )
A. B. C. D.或
[提示]数形结合,a=5,c=7,|MF|=11<a+c,M只能在右支上,N、O分别是MF、FF1的中点,结合图形,联想到中位线及双曲线定义知 |ON| = ,选B。
 『类题5』已知平面上直线
l 的方向向量 e =(- ,),点O(0,0)和A(1,-2)在 l 上的射影分别是 O´ 和 A´,且=λe,其中λ等于 ( D )
『类题5』已知平面上直线
l 的方向向量 e =(- ,),点O(0,0)和A(1,-2)在 l 上的射影分别是 O´ 和 A´,且=λe,其中λ等于 ( D )
A. B.- C.2 D.-2
『类题6』某厂2002年生产利润逐月增加,且每月增加的利润相同,但由于厂方正在改造建设,1月份投入资金恰好与该月的利润相等,随着投入资金的逐月增加,且每月增加投入的百分率相同,到12月份投入建设资金又恰好与12月份的生产利润相同,则全年的总利润W与全年总投入建设资金N的大小关系是 .
[分析]利润逐月算术增长(等差),对应于一次函数;投入逐月几何增长(等比),对应于指数函数。作出图象便知。
[例6]至2008年奥运会时,北京市区居民生活将全部用上清洁能源,居民电力消费比例由2002年的13%提高到25%,那么电力消费比例年平均增长率大约为( )
A.2% B.15.4‰ C.15.4% D.11.9%
[提示]∵(1+x)6 = = <2 (凑整),又 (1+x)6>1+6x+15x2(适当放缩),
∴15x2+6x –1<0,对应方程的根为x= (舍负),而2%<<<<15%,
∴必选D。
|
月
份 |
4 |
5 |
6 |
|
用水量(m3) |
8 |
12 |
14 |
|
水费(元) |
8 |
14 |
18 |
『类题1』 某市用水的收费方法是:水费=基本费+超额费,若每月用水量不超过最低量a米3时,只付基本费用c元,若用水量超过a米3时,除了付c元外,超过部分按b元/米3,该市某用户一个季度的用水量和支付费用如下表,则最低限量为( )
A.7m3 B.8m3 C.9m3 D.10m3
[提示]假设4月份用水量超过a m3,则
无解,得c=8,b=2,a=9,故选C。
『类题2』某招呼站,每天均有三辆开往省城南京的分为上、中、下等级的客车。某天袁先生准备在该招呼站乘车前往南京办事,但他不知道客车的车况,也不知道发车的顺序。为了尽可能乘上上等车,他采取如下策略:先放过第一辆,如果第二辆好则上第二辆,否则上第三辆。那么他乘上上等车的概率为 0.5 .
[解](列举法)
|
方
式 |
1 |
2 |
3 |
4 |
5 |
6 |
|
第1辆 |
上 |
上 |
中 |
中 |
下 |
下 |
|
第2辆 |
中 |
下 |
上 |
下 |
上 |
中 |
|
第3辆 |
下 |
中 |
下 |
上 |
中 |
上 |
|
实际乘车 |
下 |
中 |
上 |
上 |
上 |
中 |
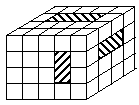 概率P ==0.5
概率P ==0.5
『类题3』 如图所示是一个的5×4×4的长方体,上面有2×1×4、2×1×5、3×1×4穿透的三个洞,那么剩下部分的体积是( )
A.50 B.54 C.56 D.58
[解]V=80-(8+10+12)+(2+3+2)-1=56,选C。
[例7]用砖砌墙,第一层(底层)用去了全部砖块的一半多一块,第二层用去了剩下的一半多一块,……,依次类推,每一层都用去了上层剩下砖块的一半多一块,如果到第九层恰好砖块用完,那么共用了 1022 块砖。
[方法一](递推归纳):第n层砌好后剩下an块砖,则共有a0块砖,且a 9 =0,a1=a0-1,a2 =a1-1=a0--1,a3=a2-1=a0---1,……,
a9=a0- (++…+ +1)=0 ,a0 =2(1-),得a0=210-2 =1022;
[方法二](分析列举):设第8层砌好后剩下x块,则x不可能为奇数,x只能为偶数且x=2,如果x是大于4的偶数,那还得继续砌下去。进行递推如下表:
|
层 数 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
用去砖块 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
|
剩下砖块 |
0 |
2 |
6 |
14 |
30 |
62 |
126 |
254 |
510 |
由表可知共有砖块512+510=1022块;
[方法三](借一还一):设第n层用砖an块,借一块砖砌第10层,a10=1,便知a1=2a2=22a3=…=29a10=29,S = a1+ a2+…+ a9=29+28+…+2 = 2 (29 -1)=1022(借的不算,为什么只借一块?);
『类题1』 ABCD-A1B1C1D1是单位正方体,黑白两个蚂蚁从点A出发沿棱爬行,每走完一条棱称为“走完一段”。白蚂蚁爬行的路线是AA1→A1D1→…,黑蚂蚁爬行的路线是AB→BB1→…,它们都遵循如下规则:所爬行的第i+2段与第i段所在直线必须是异面直线(其中i∈N+),设两蚂蚁都走完第2003段后分别停在正方体的一个顶点处,则黑白蚂蚁的距离是( )
A.1 B. C. D.0
[提示]归纳T= 6,f (2003) = f (5) ,选B。
『类题2』 5只猴子分1堆苹果,第一只猴子把苹果平均分成5堆,还多1个,把多的1个扔掉取走其中1堆;第二只猴子把剩下的苹果平均分成5堆也多1个,把多的1个扔掉也取走1堆;以后每只猴子都如此办理,则最后1只猴子所得的苹果的最小值是( )
A.1 B.624 C.255 D.625
 [解]设第n只猴子取走an个苹果,则4an = 5 an+1 +1
[解]设第n只猴子取走an个苹果,则4an = 5 an+1 +1
 an+1 +1 =
( an
+1)
an+1 +1 =
( an
+1)  an+1 +1 = ()n -1( a1 +1),
an+1 +1 = ()n -1( a1 +1),
a5 = ()4( a1 +1) –1,又a5∈N+,∴a5≥44–1 = 255,选C。
 [例4]如图,在多面体ABCDEF中,已知ABCD是边长为3的正方形,EF∥AB,EF与面AC的距离是2,且EF=
[例4]如图,在多面体ABCDEF中,已知ABCD是边长为3的正方形,EF∥AB,EF与面AC的距离是2,且EF=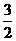 ,则该多面体的体积为( )
,则该多面体的体积为( )
A. B.5 C.6 D.
[方法1](分割法+特殊化):V=VE-AMND +VEMN-FBC =…=;
[方法2](补形法+特殊化):V=VGAD-FBC-VE-ADG =…=;
[方法3](放缩法):V>VE-ABCD = ·2·32 = 6,故选D。
『类题1』函数f (x) = Msin(ωx+φ) (ω>0) 在区间 [a,b] 上是增函数,且f (a) =-M,f (b) = M,则函数g (x) = Mcos (ωx+φ)在区间 [a,b] 上( )
A.是增函数 B.是减函数 C.可以取得最大值M D.可以取得最小值-M
[方法1](换元法):令t=ωx+φ,x∈[a,b],设t∈[-π/2,π/2]即可排除A、B、D,选C;
[方法2](特殊化):取M=ω=1,φ=0,且a = -π/2,b =π/2,满足题设;
[方法3](特殊化+图解):作出f (x) =sinx、g (x) = cos x x∈[-π/2,π/2] 即知;
[方法4](分析法): 由题设可知 [f (x)]2 + [ g (x)]2 = M2,且f (a) = -M,f (b) = M,
得g (a) = g (b) = 0,排除A、B,又f (x)在 [a,b] 上递增,从而g(x)≥0,排除D,故选C。
[小结]多种手段协同作战,如虎添翼,巧夺天工。
『类题2』椭圆 的焦点F1、F2,点P是椭圆上动点,当∠F1PF2为钝角时,点P的横坐标的取值范围是 .
[方法1]用焦半径公式,|PF1| =3 + x0,|PF2| =3 - x0,代入 |PF1|2 + |PF2|2 < |F1F2|2 得x02 < ,从而x0∈(- ,);
[方法2]用焦半径公式+特殊化,|PF1| =3 + x0,|PF2| =3 - x0,代入 |PF1|2 + |PF2|2 = |F1F2|2 得x02 = ,从而xP∈(- ,);
[方法3]用焦半径公式+椭圆定义,|PF1|2 + |PF2|2<20 (|PF1| + |PF2|)2<20 +2|PF1|·|PF2|
(|PF1| + |PF2|)2<20 +2|PF1|·|PF2|  |PF1|·|PF2| = 9 - x02 >8
|PF1|·|PF2| = 9 - x02 >8 x02 <
x02 <  x0∈(-
,);
x0∈(-
,);
[方法4]构造圆x2+y2=5,与椭圆
联立求得交点x02 =  x0∈(-
,);
x0∈(-
,);
[方法5]特殊化+椭圆定义+面积公式,20=|PF1|2 + |PF2|2=(|PF1| + |PF2|)2 -2|PF1|·|PF2|,
S△=
|PF1|·|PF2|= 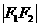 ·|y|,代入上式得|y| = ,
·|y|,代入上式得|y| = ,
代入椭圆方程得x2 =  x0∈(-
,);
x0∈(-
,);
[方法6]参数法,设P(3cosθ,2sinθ),代入 |PF1|2 + |PF2|2 < |F1F2|2 得 cos2θ< ,得x0 = 3 cosθ∈(- ,);
『开放(Ⅰ)』椭圆 的焦点F1、F2,点P为椭圆上动点,连结PF1、PF2,试尽可能多地写出一些正确的论断:
(1)a =3,b =2,c = ,e = ,p = ; (2)焦点(±,0),准线x =±;
(3)|PF1| + |PF2| = 6;
(4)P(x0,y0)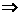 ;
;
(5)|PF1| = = 3 + x0,|PF2| = = 3 - x0;
(6)cos∠F1PF2 = -1; (7)S△= b2·tan;
(8)PF1⊥x轴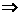 | PF1| =
;
(9)S椭圆=πab;
| PF1| =
;
(9)S椭圆=πab;
(10)a -c≤| PF|≤a+c且b2≤| PF1|+| PF2|≤a2;
『开放(Ⅱ)』 椭圆 的焦点F1、F2,点P为椭圆上动点,当∠F1PF2 =90°时,写出三个相应的正确结论 .
(11)P(,±)或(- ,±); (12)| PF1| =2或4;
(13)P点到两焦点的距离之比为2:1; (14)P点到两准线的距离之比为2:1;
(15)P点到原点的距离为; (16)S△F1PF2= 4;
『开放(Ⅲ)』 在(Ⅰ)的条件下,当P点在何处时,提出问题:
(17)S△F1PF2最大; (18)∠F1PF2最大;
(19)| PF1|·| PF2| 最大?最小? (20)∠F1PF2为直角?锐角?钝角?
(21)S△<4;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com