
题目列表(包括答案和解析)
1.若复数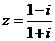 ,则z等于
,则z等于
A.-I B.i C.2i D.1+i
22.己知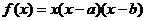 ,点A(s,f(s)),B(t,f(t)),点O是坐标原点
,点A(s,f(s)),B(t,f(t)),点O是坐标原点
(1)若a=b=1,求函数f(x)的单调递增区间;
(2)若函数f(x)的导函数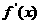 满足当
满足当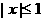 时
时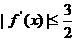 恒成立,求f(x)的解析式;
恒成立,求f(x)的解析式;
(3)若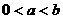 ,函数f(x)在x=s和x=t取极值,且
,函数f(x)在x=s和x=t取极值,且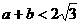 ,证明
,证明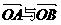 不可能垂直.
不可能垂直.
21. 已知椭圆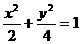 两焦点分别为F1、F2,P是椭圆在第一象限弧上一点,并满足
两焦点分别为F1、F2,P是椭圆在第一象限弧上一点,并满足
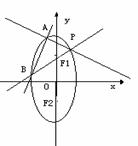
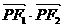 =1,过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点,
=1,过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点,
(1)求P点坐标;
(2)求证直线AB的斜率为定值;
(3)求△PAB面积的最大值.
20.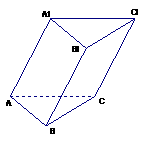 在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1
在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1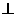 平面ABC,
平面ABC,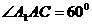 ,
,
(1)求点A1到平面ABC的距离;
(2)求AA1与平面AB1C所成角的大小;
(3)己知点D满足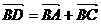 ,
,
在直线AA1上是否存在点P,使得
DP||平面AB1C,若存在,求出DP到平面
AB1C的距离,若不存在,说明理由。
19.某工厂生产某种零件,每个零件成本为40元,出厂单价为60元,该厂为鼓励销售商订购,决定当一次订购超过100个时,每多订一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂价不能低于51元。
(1)当一次订购量为多少个时,零件的实际出厂价恰为51元;
(2)设一次订购量为x个零件,实际出厂单价为P元,写出函数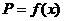 的表达式;
的表达式;
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本)
18.数列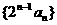 的前n项和
的前n项和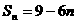
(1)求数列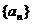 的通项公式;
的通项公式;
(2)设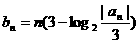 ,求数列
,求数列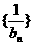 的前n项和
的前n项和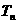 。
。
17.己知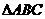 的三内角A、B、C所对的边分别是a、b、c,
的三内角A、B、C所对的边分别是a、b、c,
向量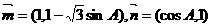 且
且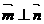 ,
,
(1)求角A;
(2)若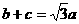 ,求
,求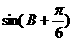 的值。
的值。
16.有一正四棱锥,它的底面边长和侧棱长均为a,现要用一张正方形的包装纸将它完全包住(不能裁剪纸,但可以折叠),那么包装纸的最小边长为 。
15.一名同学想要报考某大学,他必须从该校的7个不同专业中选出5个,并按第一志愿,第二志愿、……第五志愿的顺序填进志愿表,若专业A不能作为第一、二志愿, 则他共有 .种不同的填法。
14.对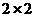 数表定义运算如下:
数表定义运算如下:
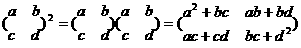 则
则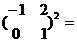 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com