
题目列表(包括答案和解析)
21.(本小题满分12分)
已知椭圆的中心在原点,焦点在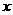 轴上,一个顶点为
轴上,一个顶点为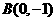 ,且其右焦点到直线
,且其右焦点到直线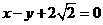 的距离为
的距离为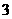 .
.
(Ⅰ) 求椭圆的方程;
(Ⅱ) 是否存在斜率为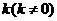 ,且过定点
,且过定点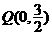 的直线
的直线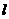 ,使
,使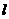 与椭圆交于两个不同的点
与椭圆交于两个不同的点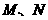 ,且
,且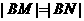 ?若存在,求出直线
?若存在,求出直线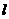 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
20.(本小题满分12分)
国际上钻石的重量计量单位为克拉.已知某种钻石的价值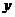 (美元)与其重量
(美元)与其重量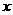 (克拉)的平方成正比,且一颗重为3克拉的该种钻石的价值为54 000美元.
(克拉)的平方成正比,且一颗重为3克拉的该种钻石的价值为54 000美元.
(Ⅰ)写出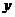 关于
关于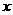 的函数关系式;
的函数关系式;
(Ⅱ)若把一颗钻石切割成重量比为1∶3的两颗钻石,求价值损失的百分率;
(Ⅲ)把一颗钻石切割成两颗钻石,若两颗钻石的重量分别为 克拉和
克拉和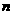 克拉,试证明:当
克拉,试证明:当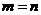
时,价值损失的百分率最大.
(注:价值损失的百分率 ;在切割过程中的重量损耗忽略不计)
;在切割过程中的重量损耗忽略不计)
18.(本小题满分12分)
已知函数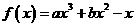 (
(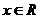 ,
,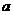 、
、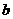 是常数,
是常数,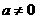 ),且当
),且当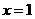 和
和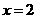 时,函数
时,函数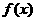 取得极值.
取得极值.
(Ⅰ)求函数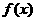 的解析式;
的解析式;
(Ⅱ)若曲线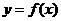 与
与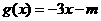 (
(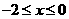 )有两个不同的交点,求实数
)有两个不同的交点,求实数 的取值范围.
的取值范围.
 19.(本小题满分12分)
19.(本小题满分12分)
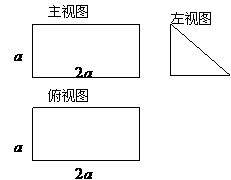
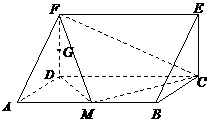
一个多面体的直观图和三视图如图所示,其中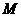 、
、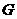 分别是
分别是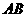 、
、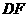 的中点.
的中点.
(Ⅰ)求证: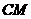
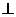 平面
平面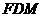 ;
;
(Ⅱ)在线段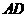 上(含
上(含 、
、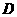 端点)确定一点
端点)确定一点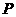 ,使得
,使得
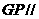 平面
平面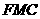 ,并给出证明;
,并给出证明;
(Ⅲ)一只小飞虫在几何体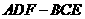 内自由飞,求它飞入几何体
内自由飞,求它飞入几何体 内的概率.
内的概率.
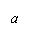
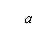
17.(本小题满分12分)
已知 ,
,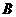 ,
,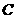 三点的坐标分别是
三点的坐标分别是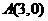 ,
,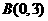 ,
,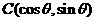 ,其中
,其中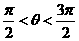 ,
,
且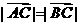 .
.
(Ⅰ)求角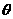 的值;
的值;
(Ⅱ)当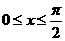 时,求函数
时,求函数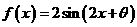 的最大值和最小值.
的最大值和最小值.
16.等差数列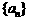 中首项为
中首项为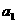 ,公差为
,公差为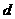 ,前
,前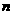 项和为
项和为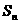 ,则下列命题中正确的有 .
,则下列命题中正确的有 .
①数列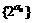 为等比数列;②若
为等比数列;②若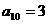 ,
,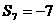 ,则
,则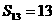 ;③
;③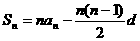 .
.
(填上所有正确命题的序号)
15.电动自行车的耗电量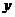 与速度
与速度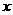 之间有如下关系:
之间有如下关系: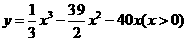 ,为使耗电量最小,则速度应为
.
,为使耗电量最小,则速度应为
.
14.函数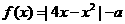 恰有三个零点,则
恰有三个零点,则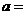 .
.
13.函数 的图象如图所示,则
的图象如图所示,则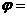 .
.
12.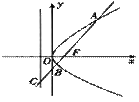 过抛物线
过抛物线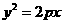 (
(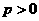 )的焦点
)的焦点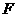 的直线
的直线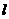 交抛物线于点
交抛物线于点 ,
,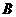 (如图所示),交其准线于点
(如图所示),交其准线于点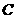 ,若
,若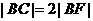 ,且
,且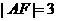 ,则此抛物线的方程为( )
,则此抛物线的方程为( )
A.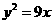 B.
B.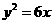 C.
C.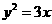 D.
D.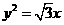
第Ⅱ卷
11.一个质地均匀的正方体骰子,六个面上分别写着1,2,3,4,5,6,现将这个骰子先后投掷两次,向上数字分别为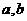 ,曲线
,曲线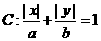 ,则曲线
,则曲线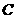 所围成的区域面积不小于50的概率是(
)
所围成的区域面积不小于50的概率是(
)
A.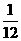 B.
B.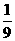 C.
C.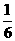 D.
D.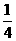
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com