
题目列表(包括答案和解析)
4、对于实数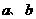 ,“
,“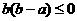 ”是“
”是“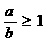 ”成立的( )
”成立的( )
(A) 充分不必要条件 (B) 必要不充分条件
(C) 充要条件 (D) 既不充分又不必要条件
3、设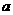 ,b是两个实数,且
,b是两个实数,且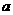 ≠b,
≠b,
①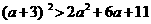 ;②
;②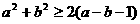 ;③
;③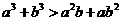 ;④
;④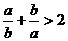 。
。
上述4个式子中恒成立的有 ( )
(A)1个 (B)2个 (C)3个 (D)4个
2、已知集合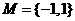 ,
,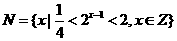 则
则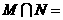 ( )
( )
(A) 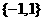 (B)
(B) 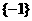 (C)
(C) 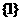 (D)
(D)
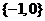
1、下列不等式正确的是( )
(A)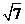 -
-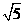 >
>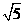 -
-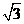 (B)
(B)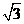 +
+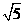 >
>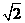 +
+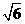
(C)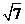 +
+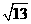 >3+
>3+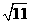 (D)5+
(D)5+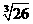 >8
>8
20. (本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分4分,第3小题满分10分.
设函数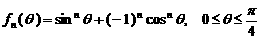 ,其中
,其中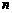 为正整数.
为正整数.
(1)判断函数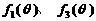 的单调性,并就
的单调性,并就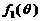 的情形证明你的结论;
的情形证明你的结论;
(2)证明: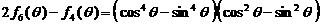 ;
;
(3)对于任意给定的正整数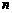 ,求函数
,求函数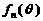 的最大值和最小值.
的最大值和最小值.
2009年上海市普通高等学校春季招生考试
19. (本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分5分,第3小题满分7分.
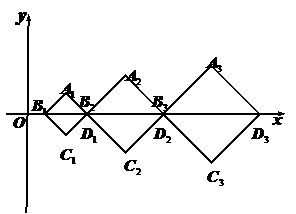
如图,在直角坐标系 中,有一组对角线长为
中,有一组对角线长为 的正方形
的正方形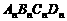
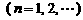 ,
,
其对角线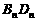 依次放置在
依次放置在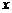 轴上(相邻顶点重合). 设
轴上(相邻顶点重合). 设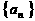 是首项为
是首项为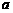 ,公差为
,公差为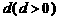 的等差数列,点
的等差数列,点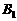 的坐标为
的坐标为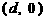 .
.
 (1)当
(1)当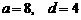 时,证明:顶点
时,证明:顶点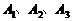 不在同一条直线上;
不在同一条直线上;
(2)在(1)的条件下,证明:所有顶点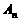 均落在抛物线
均落在抛物线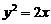 上;
上;
(3)为使所有顶点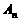 均落在抛物线
均落在抛物线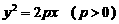 上,求
上,求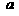 与
与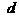 之间所应满足的关系式.
之间所应满足的关系式.
18. (本题满分14分)
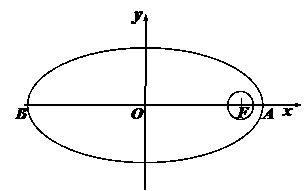 我国计划发射火星探测器,该探测器的运行轨道是以火星(其半径
我国计划发射火星探测器,该探测器的运行轨道是以火星(其半径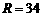 百公里)的中心
百公里)的中心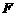 为一个焦点的椭圆. 如图,已知探测器的近火星点(轨道上离火星表面最近的点)
为一个焦点的椭圆. 如图,已知探测器的近火星点(轨道上离火星表面最近的点) 到火星表面的距离为
到火星表面的距离为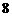 百公里,远火星点(轨道上离火星表面最远的点)
百公里,远火星点(轨道上离火星表面最远的点)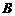 到火星表面的距离为800百公里. 假定探测器由近火星点
到火星表面的距离为800百公里. 假定探测器由近火星点 第一次逆时针运行到与轨道中心
第一次逆时针运行到与轨道中心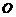 的距离为
的距离为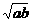 百公里时进行变轨,其中
百公里时进行变轨,其中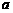 、
、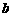 分别为椭圆的长半轴、短半轴的长,求此时探测器与火星表面的距离(精确到1百公里).
分别为椭圆的长半轴、短半轴的长,求此时探测器与火星表面的距离(精确到1百公里).
17. (本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知数列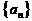 的前
的前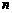 项和为
项和为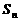 ,
,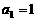 ,且
,且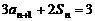 (
(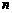 为正整数).
为正整数).
(1)求数列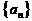 的通项公式;
的通项公式;
(2)记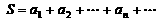 .
. 若对任意正整数
若对任意正整数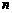 ,
,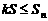 恒成立,求实数
恒成立,求实数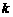 的最大值.
的最大值.
16. (本题满分12分)
(本题满分12分)
如图,在斜三棱柱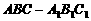 中,
中,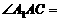
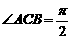 ,
,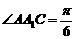 ,侧棱
,侧棱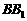 与底面所成的
与底面所成的
角为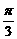 ,
,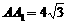 ,
,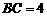 . 求斜三棱柱
. 求斜三棱柱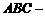
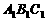
的体积 .
.
15.函数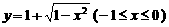 的反函数图像是
[答] ( )
的反函数图像是
[答] ( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com