
题目列表(包括答案和解析)
16、本小主要考查等比数列、数列求和等基础知识,考查运算求解能力。满分13分
解:(Ⅰ) 设等比数列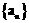 的公比为q。
的公比为q。
依题意,得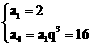 ……………………………………………… 2分
……………………………………………… 2分
解得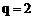 , ……………………………………………………………… 4分
, ……………………………………………………………… 4分
∴数列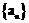 的通项公式:
的通项公式: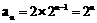 。 ………………………… 7分
。 ………………………… 7分
(Ⅱ) 由(Ⅰ)得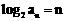 ,
,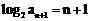 。
。
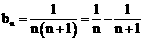 。 ……………………………………………… 10分
。 ……………………………………………… 10分
∴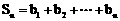
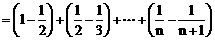
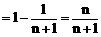 。 ………………………………………………… 13分
。 ………………………………………………… 13分
16、(本小题满分13分)
在等比数列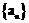 中,
中,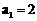 ,
,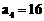 。
。
(Ⅰ)求数列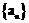 的通项公式;
的通项公式;
(Ⅱ)令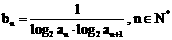 ,求数列
,求数列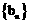 的前n项和
的前n项和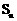 。
。
11、9 12、5 13、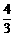 14、
14、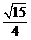 15、
15、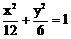
21.本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分。
如果多做,则按所做的前两题计分。作答时,先用2B铅笔在答题卡上把所选题目对应
的题号涂黑,并将所选题号填入括号中。
(1)(本小题满分7分)选修4-2:矩阵与变换
已知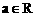 ,矩阵
,矩阵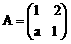 对应的线性变换把点
对应的线性变换把点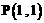 变成点
变成点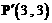 ,
,
求矩阵A的特征值以及属于每个特征值的一个特征向量。
(2)(本小题满分7分)选修4-4:坐标系与参数方程
已知直线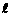 经过点
经过点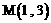 ,且倾斜角为
,且倾斜角为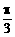 ,圆C的参数方程为
,圆C的参数方程为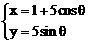 (
(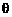
是参数)。直线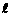 与圆C交于
与圆C交于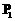 、
、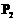 两点,求
两点,求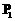 、
、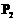 两点间的距离。
两点间的距离。
(3)(本小题满分7分)选修4-5:不等式选讲
解不等式: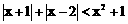 。
。
2009年福建省普通高中毕业班质量检查
理科数学试题参考解答及评分标准
说明:
20.(本小题满分14分)
已知函数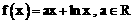
(Ⅰ)求函数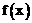 的极值;
的极值;
(Ⅱ)对于曲线上的不同两点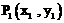 ,
,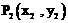 ,如果存在曲线上的点
,如果存在曲线上的点
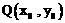 ,且
,且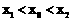 ,使得曲线在点
,使得曲线在点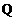 处的切线
处的切线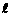 ∥
∥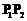 ,则称
,则称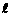 为弦
为弦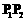 的伴随切线。特别地,当
的伴随切线。特别地,当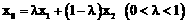 时,又称
时,又称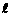 为
为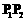 的λ-
的λ-
伴随切线。
(ⅰ)求证:曲线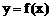 的任意一条弦均有伴随切线,并且伴随切线是唯一的;
的任意一条弦均有伴随切线,并且伴随切线是唯一的;
(ⅱ)是否存在曲线C,使得曲线C的任意一条弦均有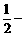 伴随切线?若存在,给
伴随切线?若存在,给
出一条这样的曲线 ,并证明你的结论; 若不存在 ,说明理由。
19.(本题满分13分)
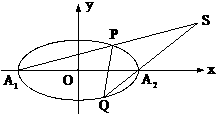 已知椭圆C的离心率
已知椭圆C的离心率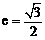 ,长轴的左右端点分
,长轴的左右端点分
别为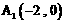 ,
,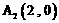 。
。
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线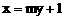 与椭圆C交于P、Q两
与椭圆C交于P、Q两
点,直线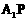 与
与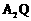 交于点S。试问:当
交于点S。试问:当
m变化时,点S是否恒在一条定直线上?
若是,请写出这条直线方程,并证明你的结论;若不是,请说明理由。
18.(本小题满分13分)
四棱锥P-ABCD的底面与四个侧面的形状和大小如图所示。
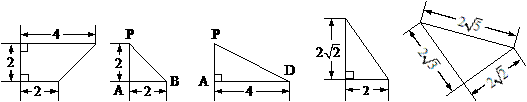
(Ⅰ)写出四棱锥P-ABCD中四对线面垂直关系(不要求证明);
(Ⅱ)在四棱锥P-ABCD中,若E为PA的中点,求证:BE∥平面PCD;
(Ⅲ)在四棱锥P-ABCD中,设面PAB与面PCD所成的角为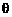
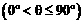 ,求
,求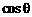
的值
17.(本小题满分13分)
甲、乙两位学生参加数学竞赛培训。现分别从他们在培训期间参加的若干次预赛成绩中
随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(Ⅰ)用茎叶图表示这两组数据;
(Ⅱ)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参
加合适?请说明理由;
(Ⅲ)若将频率视为概率,对甲同学在今后的3次数学竞赛成绩进行预测,记这3次成
绩中高于80分的次数为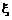 ,求
,求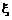 的分布列及数学期望
的分布列及数学期望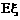 。
。
16.(本小题满分13分)
在等比数列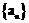 中,
中,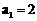 ,
,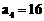 。
。
(Ⅰ)求数列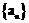 的通项公式;
的通项公式;
(Ⅱ)令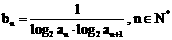 ,求数列
,求数列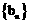 的前n项和
的前n项和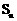 。
。
15.已知椭圆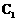 的中心在原点、焦点在x轴上,抛物线
的中心在原点、焦点在x轴上,抛物线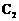 的顶点在原点、焦点在x轴上。
的顶点在原点、焦点在x轴上。
小明从曲线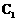 、
、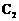 上各取若干个点(每条曲线上至少取两个点),并记录其坐标
上各取若干个点(每条曲线上至少取两个点),并记录其坐标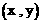 。
。
由于记录失误,使得其中恰有一个点既不在椭圆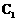 上,也不在抛物线
上,也不在抛物线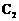 上。小明的记
上。小明的记
录如下:
 |
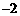 |
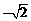 |
0 |
2 |
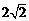 |
3 |
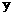 |
2 |
0 |
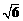 |
错误!不能通过编辑域代码创建对象。 |
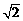 |
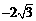 |
据此,可推断椭圆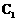 的方程为_______________。
的方程为_______________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com