
题目列表(包括答案和解析)
15.(本小题满分14分)
(3)[解]由(1)知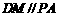 ,由(2)知PA⊥平面PBC, ∴DM⊥平面PBC.……11分
,由(2)知PA⊥平面PBC, ∴DM⊥平面PBC.……11分
∵正三角形PDB中易求得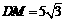 ,
,
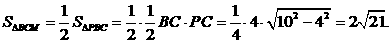 ……13分
……13分
∴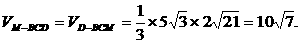 ……14分
……14分
20.(本小题满分16分)
已知函数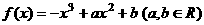 .
.
(I)当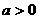 时,求函数
时,求函数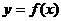 的极值;
的极值;
(II) 若函数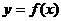 的图象上任意不同的两点连线的斜率都小于2,求证:
的图象上任意不同的两点连线的斜率都小于2,求证: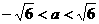 ;
;
(III)对任意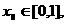
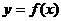 的图像在
的图像在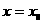 处的切线的斜率为
处的切线的斜率为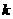 ,求证:
,求证: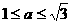 是
是 成立的充要条件.
成立的充要条件.
19.(本小题满分16分)
已知数列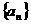 中,
中,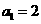 ,
,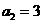 ,其前
,其前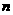 项和
项和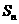 满足
满足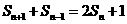
其中( ,
,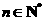 ).
).
(1)求数列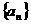 的通项公式;
的通项公式;
(2)设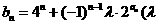 为非零整数,
为非零整数,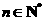 ),试确定
),试确定 的值,使得对任意
的值,使得对任意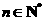 ,都有
,都有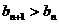 成立.
成立.
18.(本小题满分15分)
已知圆 的方程为
的方程为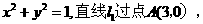 且与圆
且与圆 相切.
相切.
(1)求直线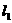 的方程;
的方程;
(2)设圆 与
与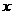 轴交与
轴交与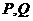 两点,M是圆
两点,M是圆 上异于
上异于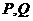 的任意一点,过点
的任意一点,过点 且与
且与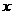 轴垂直的直线为
轴垂直的直线为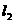 ,直线
,直线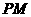 交直线
交直线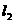 于点
于点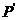 ,直线
,直线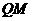 交直线
交直线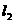 于点
于点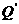 .求证:以
.求证:以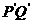 为直径的圆
为直径的圆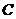 总过定点,并求出定点坐标.
总过定点,并求出定点坐标.
17.(本小题满分15分)
某工厂有216名工人接受了生产1000台GH型高科技产品的总任务,已知每台GH型产品由4个G型装置和3个H型装置配套组成.每个工人每小时能加工6个G型装置或3个H型装置.现将工人分成两组同时开始加工,每组分别加工一种装置.设加工G型装置的工人有x人,他们加工完G型装置所需时间为g(x),其余工人加工完H型装置所需时间为h(x)(单位:小时,可不为整数).
(1)写出g(x),h(x)的解析式;
(2)比较g(x)与h(x)的大小,并写出这216名工人完成总任务的时间f(x)的解析式;
(3)应怎样分组,才能使完成总任务用的时间最少?
16.(本小题满分14分)
已知函数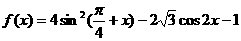 且给定条件
且给定条件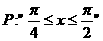
(Ⅰ)在条件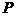 下求
下求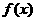 的最大值及最小值;
的最大值及最小值;
(Ⅱ)若又给条件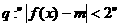 且
且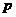 是
是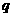 的充分条件,求实数
的充分条件,求实数 的取值范围.
的取值范围.
15.(本小题满分14分)
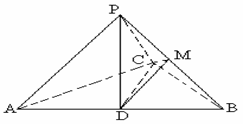 如图,已知三棱锥
如图,已知三棱锥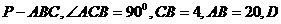 为
为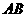 中点,
中点,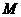 为
为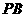 的中点,且
的中点,且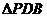 是正三角形,
是正三角形,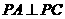 .
.
(I)求证: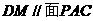 ;
;
(II)求证:平面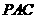 ⊥平面
⊥平面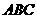 ;
;
(Ⅲ)求三棱锥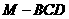 的体积.
的体积.
14.已知: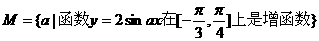 ,
,
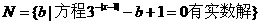 ,设
,设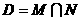 ,且定义在
,且定义在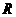 上的奇函数
上的奇函数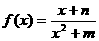 在
在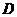 内没有最小值,则
内没有最小值,则 的取值范围是 ▲ .
的取值范围是 ▲ .
13.执行右边的程序框图,若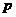 =0.9,则输出的
=0.9,则输出的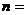 ▲ .
▲ .
12.若正方形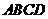 边长为1,点
边长为1,点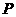 在线段
在线段 上运动, 则
上运动, 则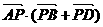 的最大值是 ▲ .
的最大值是 ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com