
题目列表(包括答案和解析)
18.(本题满分12分)口袋中有质地、大小完全相同的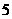 个球,编号分别为
个球,编号分别为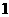 、
、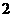 、
、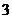 、
、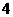 、
、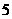 ,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢。
,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢。
(1)求两个编号的和为6的概率;
(2)求甲赢的事件发生的概率。
18. 解:(1)设未被选中的概率为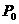 ,
,
则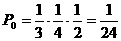 ………………4分
………………4分
(2)(理)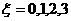
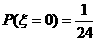 ,
,
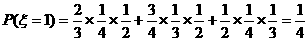 ……7分
……7分
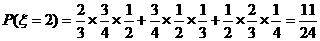 ……9分
……9分
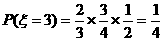 ……11分
……11分
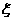 的分布列为:
的分布列为:
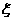 |
0 |
1 |
2 |
3 |
|
P |
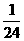 |
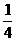 |
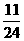 |
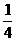 |
E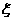 =
=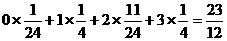 ……12分
……12分
(文)被两家单位录用的概率为: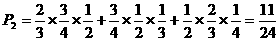 ……7分
……7分
被三家单位录用的概率为: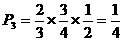 ……10分
……10分
所以至少被两家单位录用的概率为: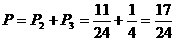 ……12分
……12分
安庆市示范高中2010届高三上学期四校元旦联考高三数学(文)测试
18.(本题满分12分)
大学毕业生小明到甲、乙、丙三个单位应聘,其被录用的概率分别为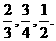 (各单位是否录用他相互独立,允许小明被多个单位同时录用)
(各单位是否录用他相互独立,允许小明被多个单位同时录用)
(1)求小明没有被录用的概率;
(2)(理)设录用小明的单位个数为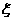 ,求
,求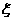 的分布列和它的数学期望。
的分布列和它的数学期望。
(文)求小明至少被两个单位录用的概率。
18.用一个不平行于圆柱底面的平面截圆柱成一个“斜截圆柱”,如图所示,已知圆柱底面半径为r,圆柱的母线被平面截下的线段称为“部分母线”, 斜截圆柱面上最短的部分母线AD=r,最长的部分母线BC=3r;A点在底面圆周上沿逆时针方向旋转一个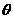 角到
角到 ,对应一条部分母线
,对应一条部分母线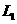 ,再旋转
,再旋转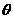 角到
角到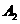 ,对应一条部分母线
,对应一条部分母线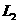 …,这样可以得到一系列部分母线
…,这样可以得到一系列部分母线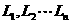 ;
;
(1)  当
当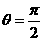 时,求
时,求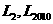 的长度;
的长度;
(2) 当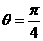 时,尝试求
时,尝试求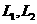 的长度,请写出
的长度,请写出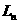 的一般表达式
的一般表达式
(3) 将斜截圆柱侧面从AD截开,并沿与AD垂直的水平方向展开,得到一个平面图形M,试研究该侧面展开图M的几何特征,提出两个你认为最有价值的问题,并予以解答。
17. 如图,正三角形ABC边长为1,将各边中点连成的三角形挖去,得到图1所示阴影部分,我们将此变换记为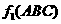 ,经2次变换
,经2次变换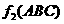 得到的图形如图2所示.经n次变换
得到的图形如图2所示.经n次变换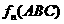 所得到图形的面积记为
所得到图形的面积记为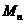 ,所有被挖去的三角形的边长之和记为
,所有被挖去的三角形的边长之和记为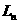
(1)求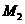 和相应的镂空区域边界长
和相应的镂空区域边界长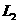
(2)研究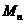 、
、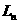 随n变化的规律
随n变化的规律
(3)将经变换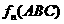 所得到图形沿与该平面成
所得到图形沿与该平面成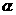 角的单位向量平行移动得到的几何体体积记为
角的单位向量平行移动得到的几何体体积记为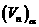 ,如图3所示的几何体体积为
,如图3所示的几何体体积为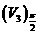 ,问是否存在
,问是否存在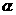 ,使得
,使得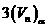 =
=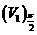 ,若存在,求出
,若存在,求出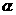 ,若不存在,请说明理由。
,若不存在,请说明理由。
16.设函数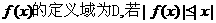 对任意的实数
对任意的实数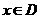 均成立,则称函数
均成立,则称函数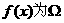 函数。
函数。
(1)函数 是
是 函数吗?请说明理由;
函数吗?请说明理由;
(2)若函数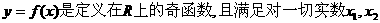 ,均有
,均有
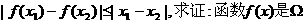 函数;
函数;
(3)请写出一个形如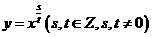 的
的 函数,并研究它的性质。
函数,并研究它的性质。
15.如果将函数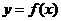 的图像以原点为中心逆时针旋转
的图像以原点为中心逆时针旋转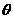 角(
角(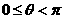 )后,所得到的图形仍是一个新的函数
)后,所得到的图形仍是一个新的函数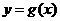 的图像,则称
的图像,则称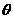 为函数
为函数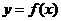 的一个“自由角”,设
的一个“自由角”,设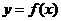 的图像是曲线C:
的图像是曲线C: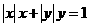
(1)写出函数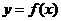 的表达式
的表达式
(2)试求函数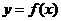 的“自由角”的取值范围
的“自由角”的取值范围
(3)请设定一个特殊的“自由角”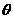 ,研究所得新函数
,研究所得新函数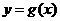 的性质
的性质
14.已知曲线C: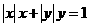 和直线
和直线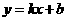
(1)当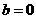 时,曲线C与直线有且仅有一个交点,求
时,曲线C与直线有且仅有一个交点,求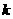 的取值范围
的取值范围
(2)当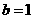 时,就
时,就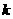 的不同取值讨论曲线与直线的交点情况
的不同取值讨论曲线与直线的交点情况
(3)对于定义在D上的单调函数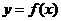 ,如果存在区间
,如果存在区间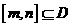 ,使得
,使得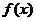 在
在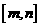 上的值域为
上的值域为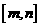 ,则称该函数为“闭合函数”;试研究曲线C能否成为闭合函数的图像,如果能,求出其闭合区间
,则称该函数为“闭合函数”;试研究曲线C能否成为闭合函数的图像,如果能,求出其闭合区间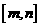 ,如不能,说明理由
,如不能,说明理由
13.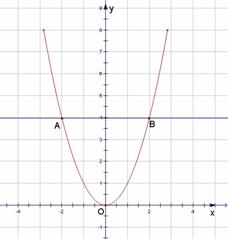 如果
如果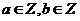 ,则称点M
,则称点M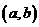 为整点,如图,直线
为整点,如图,直线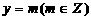 与抛物线
与抛物线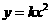 相交,组成封闭图形AOB,该图形内部包括边界线上整点个数记为
相交,组成封闭图形AOB,该图形内部包括边界线上整点个数记为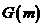
(1) 若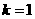 ,
,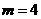 ,求
,求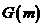
(2) 当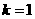 ,
,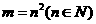 时,求
时,求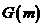 的一般表达式
的一般表达式
(3) 请设定 与
与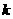 的一个关系
的一个关系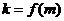 ,研究
,研究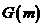 的变化规律,写出你的研究结论和过程。
的变化规律,写出你的研究结论和过程。
12.已知方程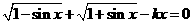 至少有4个正数解,则k的取值范围是
.
至少有4个正数解,则k的取值范围是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com