
题目列表(包括答案和解析)
10. 在正三棱柱ABC-A1B1C1中,若AB=2,A A1=1,则点A到平面A1BC的距离为( B )
A.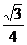 B.
B.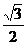 C.
C.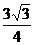 D.
D.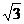
[解析]如图,取 中点
中点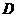 ,连
,连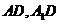 ,
,
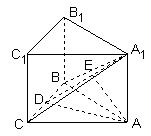
∵ABC-A1B1C1是正三棱柱,∴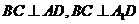 ,
,
∴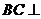 平面
平面 ,在平面
,在平面 内作
内作 于
于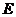 ,
,
则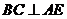 ,∴
,∴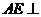 平面
平面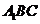 ,∴
,∴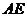 就是所求的距离.
就是所求的距离.
由已知可得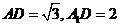 ,∴
,∴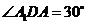 ,
,
在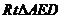 中,得
中,得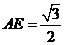 .
.
9. 设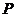 是
是 的二面角
的二面角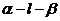 内一点,
内一点,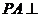 平面
平面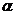 ,
,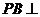 平面
平面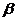 ,
,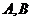 分别为垂足,
分别为垂足,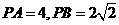 ,则
,则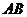 的长是 ( C )
的长是 ( C )
A.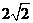 B.
B. 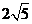 C.
C.
 D.
D. 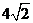
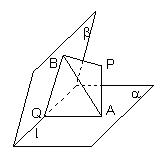
[解析]如图,平面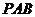 与
与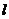 交于
交于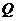 ,连
,连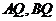 ,则
,则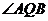 为二面角的平面角,所以
为二面角的平面角,所以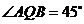 ,从而
,从而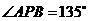 ,
,
在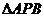 中,由余弦定理可得
中,由余弦定理可得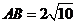 .
.
8. 正三棱柱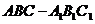 中,底面边长为2,若直线
中,底面边长为2,若直线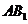 与平面
与平面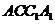 所成角为
所成角为 ,则棱柱的高为
( C )
,则棱柱的高为
( C )
A.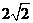 B.2 C.
B.2 C.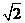 D.1
D.1
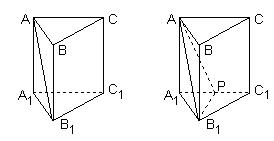
题干图 解答图
[解析]如图,取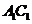 的中点
的中点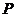 ,连接
,连接 、
、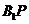 ,易得
,易得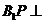 平面
平面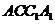 ,
, 是
是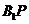 在平面
在平面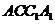 内的射影,所以
内的射影,所以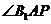 是所求的角.
是所求的角.
设棱柱的高为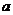 ,即
,即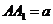 .
.
又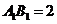 ,在
,在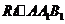 中,解得
中,解得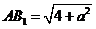 .
.
在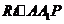 中,得
中,得 ,则在
,则在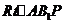 中,
中,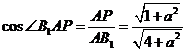 .
.
又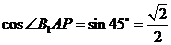 ,所以
,所以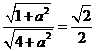 ,解得
,解得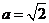 .
.
7.已知向量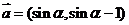 ,
, 则
则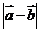 的范围是( D )
的范围是( D )
A.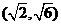 B.
B. C.
C.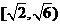 D.
D.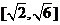
[解析]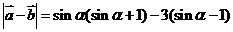
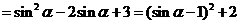
∵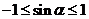 ,∴
,∴ ,
, ,
,
∴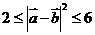 ,
,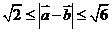 .
.
6. 已知 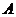 船在灯塔
船在灯塔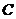 北偏东
北偏东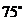 且
且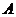 到
到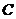 的距离为
的距离为 ,
,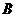 船在灯塔
船在灯塔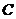 西偏北
西偏北 且
且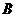 到
到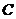 的距离为
的距离为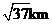 ,则
,则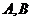 两船的距离为 ( C
)
两船的距离为 ( C
)
A.  B.
B.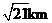 C.
C.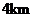 D.
D.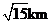
[解析]如图,由题意可知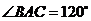 ,
,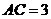 ,
,
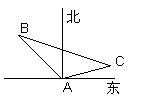
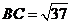 ,由余弦定理,得
,由余弦定理,得
 ,代入数据,化简得
,代入数据,化简得
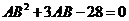 ,解得
,解得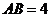 (舍去
(舍去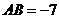 ).
).
5. 钝角△ABC中,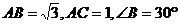 ,则
,则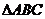 的面积等于 ( B )
的面积等于 ( B )
A.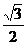 B.
B.
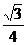 C.
C.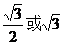 D.
D.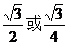
[解析]由正弦定理得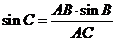
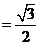 ,∴
,∴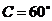 (舍去)或
(舍去)或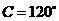 ,
,
∴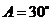 ,
,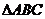 的面积为
的面积为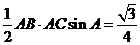 .
.
4.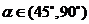 ,
,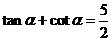 ,则
,则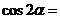 ( A )
( A )
A.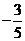 B.
B. 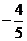 C.
C.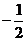 D.
D. 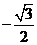
[解析]由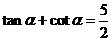 解得
解得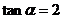 ,∴
,∴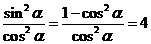 ,
,
解得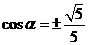 ,∵
,∵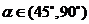 ,∴
,∴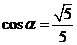 ,
,
∴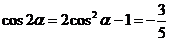
3. 已知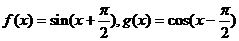 ,则
,则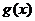 的图象 ( C )
的图象 ( C )
A.与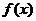 的图象相同
B.与
的图象相同
B.与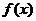 的图象关于
的图象关于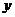 轴对称
轴对称
C.向左平移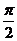 个单位,得到
个单位,得到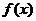 的图象 D.向右平移
的图象 D.向右平移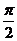 个单位,得到
个单位,得到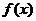 的图象
的图象
[解析]化简得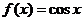 ,
,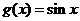 ,易知C正确.
,易知C正确.
2. 已知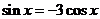 ,则
,则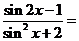 ( B )
( B )
A.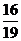 B.
B.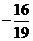 C.
C.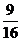 D.
D.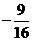
[解析]方法一:∵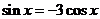
∴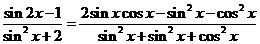
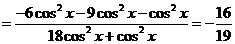 .
.
方法二:∵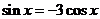 ,∴
,∴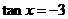 .
.
∴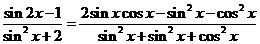
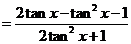
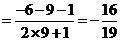 .
.
1.已知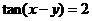 ,
,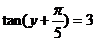 ,则
,则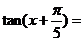 ( C )
( C )
A.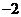 B.
B.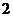 C.
C.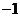 D.
D.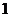
[解析]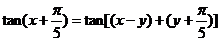

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com