
题目列表(包括答案和解析)
7.已知a、b∈R,a+b+a2+b2=24,则a+b的取值范围是_________________.
解析:∵a2+b2≥2ab,当且仅当a=b时取“=”,
∴2(a2+b2)≥(a+b)2,即a2+b2≥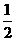 (a+b)2,当且仅当a=b时取“=”.
(a+b)2,当且仅当a=b时取“=”.
∴24-(a+b)=a2+b2≥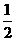 (a+b)2,当且仅当a=b时取“=”,
(a+b)2,当且仅当a=b时取“=”,
即(a+b)2+2(a+b)-48≤0.
解关于a+b的二次不等式,得-8≤a+b≤6.
答案:-8≤a+b≤6
6.一批货物随17列货车从A市以a km/h匀速直达B市,已知两地铁路线长400 km,为了安全,两列车之间的距离不得小于(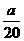 )2 km,那么这批货物全部运到B市,最快需要
)2 km,那么这批货物全部运到B市,最快需要
( )
A.6 h B.8 h C.10 h D.12 h
解析:第一列货车到达B市的时间为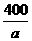 h,由于两列货车的间距不得小于(
h,由于两列货车的间距不得小于(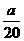 )2 km,所以第17列货车到达时间为
)2 km,所以第17列货车到达时间为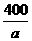 +
+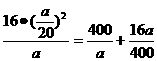 ≥8,当且仅当
≥8,当且仅当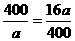 ,即a=100(km/h)时成立,所以最快需要8
h,故选择B.
,即a=100(km/h)时成立,所以最快需要8
h,故选择B.
答案:B
5.若实数a、b满足a+b=2,则3a+3b的最小值是( )
A.18 B.6 C.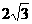 D.
D.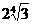
解析:由均值不等式,得3a+3b≥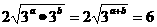 ,当且仅当a=b=1时取等号,所以3a+3b的最小值是6,故选B.
,当且仅当a=b=1时取等号,所以3a+3b的最小值是6,故选B.
答案:B
4.某学生用一不准确的天平(两臂不等长)称10 g药品,他先将5 g的砝码放在左盘,将药品放在右盘使之平衡;然后又将5 g的砝码放在右盘,将药品放于左盘使之平衡,则此学生实际所得药品( )
A.小于10 g B.大于10 g C.大于等于10 g D.小于等于10 g
解析:设左、右臂长分别为t1、t2,第一次称的药品为x1,第二次称的药品为x2,则有5t1=x1t2,x2t1=5t2,所以x1+x2=5(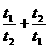 )>5×2=10,即大于10g.
)>5×2=10,即大于10g.
答案:B
3.若a,b都是正实数,π是圆周率,e是自然对数的底数,则下列各式中可能大于a2+b2的是( )
A.2(a+b-1) B.(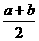 )2+ab C.
)2+ab C.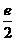 (a+b) D.
(a+b) D.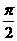 ab
ab
解析:对于A,因为a2+b2-2(a+b-1)=(a-1)2+(b-1)2≥0,因此a2+b2≥2(a+b-1);对于B,a2+b2-[(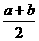 )2+ab]=
)2+ab]=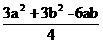 =
=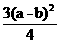 ≥0,因此a2+b2≥(
≥0,因此a2+b2≥(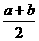 )2+ab;对于D,因为a2+b2≥2ab>
)2+ab;对于D,因为a2+b2≥2ab>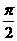 ab,所以a2+b2>
ab,所以a2+b2>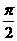 ab.
ab.
综上,可知只有C满足条件.
答案:C
2.下列结论正确的是( )
A.当x>0且x≠1时,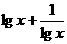 ≥2
≥2
B.当x>0时,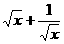 ≥2
≥2
C.当x≥2时,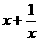 的最小值是2
的最小值是2
D.当0<x≤2时,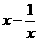 无最大值
无最大值
解析: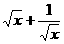 ≥
≥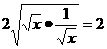 ,当且仅当
,当且仅当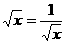 ,即x=1时等号成立.
,即x=1时等号成立.
答案:B
1.设x,y∈R,则“x2+y2≤1”是“|x|+|y|≤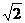 ”成立的( )
”成立的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:∵2|x||y|≤|x|2+|y|2=x2+y2≤1,
∴(|x|+|y|)2=x2+2|x||y|+y2≤2.
∴|x|+|y|≤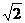 .
.
取x=0,y=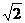 ,不满足x2+y2≤1,故是充分不必要条件.
,不满足x2+y2≤1,故是充分不必要条件.
答案:A
12.已知集合A={x|x2-6x+8<0},B={x|(x-a)(x-3a)<0}.
(1)若A B,求a的取值范围;
B,求a的取值范围;
(2)若A∩B={x|3<x<4},求a的取值范围.
解:由题意,知A={x|2<x<4},
(1)当a>0时,B={x|a<x<3a},
∴应满足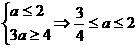 .
.
当a<0时,B={x|3a<x<a},
∴应满足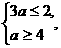 无解.
无解.
当a=0时,B=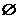 ,显然不符合条件.
,显然不符合条件.
∴若A B,则a的取值范围为[
B,则a的取值范围为[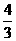 ,2].
,2].
(2)要满足A∩B={x|3<x<4},显然a>0,
∴B={x|a<x<3a}.
∴a=3,B={x|3<x<9}.
从而A∩B={x|3<x<4},故所求的a值为3.
11.已知集合A={x|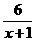 ≥1,x∈R},B={x|x2-2x-m<0}.
≥1,x∈R},B={x|x2-2x-m<0}.
(1)当m=3时,求A∩(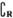 B);
B);
(2)若A∩B={x|-1<x<4},求实数m的值.
解:由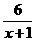 ≥1,得
≥1,得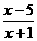 ≤0,
≤0,
∴-1<x≤5.
∴A={x|-1<x≤5}.
(1)当m=3时,B={x|-1<x<3},
则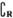 B={x|x≤-1或x≥3}.
B={x|x≤-1或x≥3}.
∴A∩(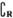 B)={x|3≤x≤5}.
B)={x|3≤x≤5}.
(2)∵A={x|-1<x≤5},A∩B={x|-1<x<4},
∴x=4是方程x2-2x-m=0的根.
∴42-2×4-m=0,解得m=8.
此时B={x|-2<x<4},符合题意,故实数m的值为8.
10.设集合A={(x,y)|y≥|x-2|,x≥0},B={(x,y)|y≤-x+b},A∩B≠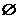 .
.
(1)则b的取值范围是_________________;
(2)若(x,y)∈A∩B,且x+2y的最大值为9,则b的值是_________________.
解析:(1)由图象可知,集合A表示的区域为图中的阴影部分,又A∩B≠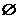 ,∴b的取值范围是[2,+∞);(2)若(x,y)∈A∩B,则(x,y)在图中的四边形内,且z=x+2y在(0,b)处取得最大值,
,∴b的取值范围是[2,+∞);(2)若(x,y)∈A∩B,则(x,y)在图中的四边形内,且z=x+2y在(0,b)处取得最大值,
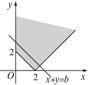
∴0+2b=9.∴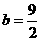 .
.
答案:(1)[2,+∞)(2)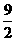
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com