
题目列表(包括答案和解析)
23.(本题满分10分)
(Ⅰ)直线的直角坐标方程为: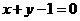 ;
;
………………3分
(Ⅱ)原点到直线的距离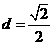 ,
,
直线参数方程为: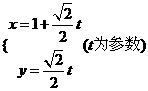 曲线
曲线 的直角坐标方程为:
的直角坐标方程为: ,
,
联立得: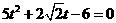 ,求得
,求得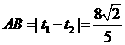
所以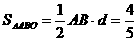 …………………………10分
…………………………10分
23.(本小题满分10分)选修4-4:坐标系与参数方程
已知直线 的极坐标方程为
的极坐标方程为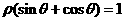 ,曲线
,曲线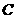 的参数方程为
的参数方程为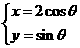 (
(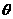 为参数).
为参数).
(Ⅰ)求直线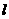 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线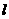 与曲线
与曲线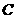 交于,四两点,原点为
交于,四两点,原点为 ,求
,求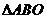 的面积.
的面积.
22.(本题满分10分)
(Ⅰ) 证明:
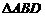 ∽
∽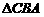
∴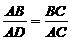 ,即
,即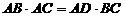 ……………………4分
……………………4分
(Ⅱ)由射影定理知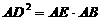
又由三角形相似可知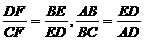 ,且
,且
∴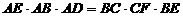 ,结合射影定理
,结合射影定理
∴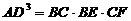 …………
………… 分
分
22.(本小题满分10分)选修4-1:几何证明选讲
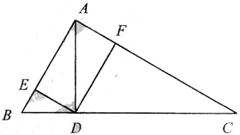 已知
已知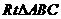 中,
中,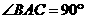 ,
,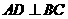 ,
,
垂足为,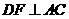 ,垂足为,
,垂足为,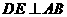 ,
,
垂足为.
求证:(Ⅰ)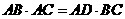 ;
;
(Ⅱ)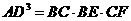
21. (本题满分12分)
(Ⅰ)由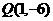 在抛物线
在抛物线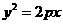 上可得,
上可得,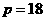 ,抛物线方程为
,抛物线方程为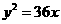 ………1分
………1分
设抛物线 的切线方程为:
的切线方程为: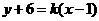
联立,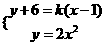 ,由
,由 ,可得
,可得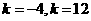
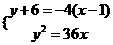 可知
可知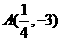
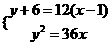 可知
可知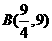 ……………………3分
……………………3分
易求直线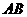 方程为
方程为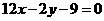 ………………………4分
………………………4分
弦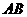 长为
长为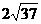 ……………………5分
……………………5分
(Ⅱ)设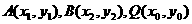 ,三个点都在抛物线
,三个点都在抛物线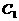 上,故有
上,故有
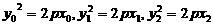 ,作差整理得
,作差整理得
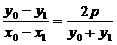 ,
,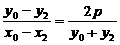
所以直线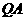 :
: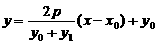 ,直线
,直线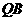 :
: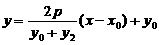
…………………6分
因为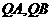 均是抛物线
均是抛物线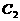 的切线,故与抛物线
的切线,故与抛物线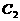 方程联立,
方程联立,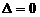 ,可得:
,可得:
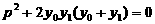 ,
,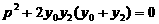
两式相减整理得: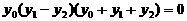 ,即可知
,即可知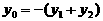
……………………8分
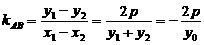
所以直线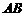 :
: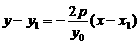 ,与抛物线
,与抛物线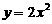 联立消去
联立消去
得关于的一元二次方程: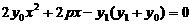 ……………………10分
……………………10分
易知其判别式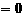 ,因而直线
,因而直线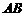 与抛物线
与抛物线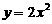 相切.故直线
相切.故直线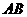 与抛物线
与抛物线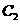 相切.
相切.
…………………………………………12分
21.(本小题满分12分)
已知点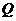 是抛物线
是抛物线 :
: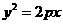 (
(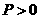 )上异于坐标原点
)上异于坐标原点 的点,过点
的点,过点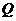 与抛物线
与抛物线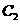 :
: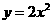 相切的两条直线分别交抛物线
相切的两条直线分别交抛物线 于点A,B.
于点A,B.
(Ⅰ)若点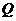 的坐标为
的坐标为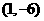 ,求直线
,求直线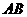 的方程及弦
的方程及弦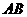 的长;
的长;
(Ⅱ)判断直线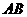 与抛物线
与抛物线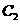 的位置关系,并说明理由.
的位置关系,并说明理由.
20.(本题满分12分)
(Ⅰ) 设
设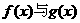 交于点
交于点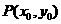 ,则有
,则有
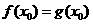 ,即
,即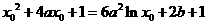
 (1)
(1)
又由题意知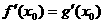 ,即
,即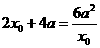 (2)
……2分
(2)
……2分
由(2)解得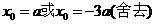
将 代入(1)整理得
代入(1)整理得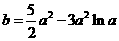 …………………………4分
…………………………4分
令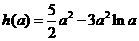 ,则
,则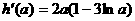
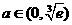 时,
时,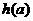 递增,
递增,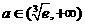 时
时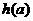 递减,所以
递减,所以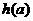
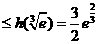
即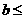
 ,
,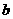 的最大值为
的最大值为 ……………………………………6分
……………………………………6分
(Ⅱ)不妨设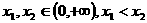 ,
,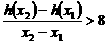 变形得
变形得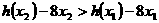
令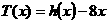 ,
,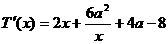 ,
,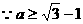 ,
,
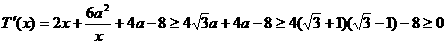
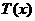 在
在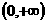 内单调增,
内单调增,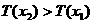 ,同理可证
,同理可证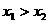 命题成立
命题成立
……………………12分
20.(本小题满分12分)
已知定义在正实数集上的函数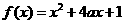 ,
,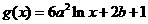 ,其中
,其中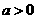 .
.
(Ⅰ)设两曲线 ,
,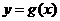 有公共点,且在该点处的切线相同,用表示
有公共点,且在该点处的切线相同,用表示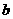 ,并求
,并求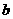 的最大值;
的最大值;
(Ⅱ)设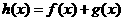 ,证明:若
,证明:若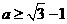 ,则对任意
,则对任意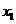 ,
,
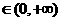 ,
,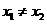 有
有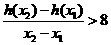 .
.
22.解:(1)由题意,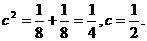
所以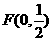 ,抛物线D的标准方程为
,抛物线D的标准方程为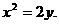 …………3分
…………3分
(2)设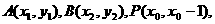
由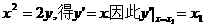
抛物线D在点A处的切线方程为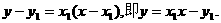 …………4分
…………4分
而A点处的切线过点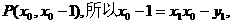
即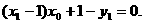
同理,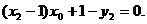
可见,点A,B在直线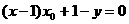 上.
上.
令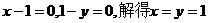
所以,直线AB过定点Q(1,1) …………6分
(3)设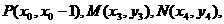
 直线PQ的方程为
直线PQ的方程为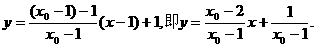
由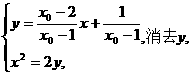
得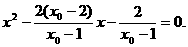
由韦达定理,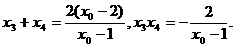 …………9分
…………9分
而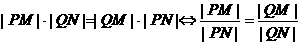
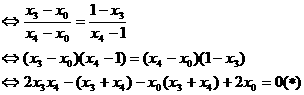
…………12分
将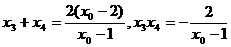 代入方程(*)的左边,得
代入方程(*)的左边,得
(*)的左边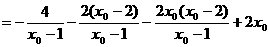
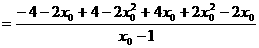
=0.
因而有|PM|·|QN|=|QM|·|PN|. …………14分
22.(本题满分14分)
抛物线D以双曲线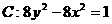 的焦点
的焦点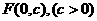 为焦点.
为焦点.
(1)求抛物线D的标准方程;
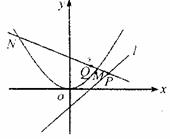
(2)过直线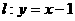 上的动点P作抛物线D的两条切线,切点为A,B.求证:直线AB过定点Q,并求出Q的坐标;
上的动点P作抛物线D的两条切线,切点为A,B.求证:直线AB过定点Q,并求出Q的坐标;
(3)在(2)的条件下,若直线PQ交抛物线D于M,N两点,求证:|PM|·|QN|=|QM|·|PN|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com