
题目列表(包括答案和解析)
3.若方程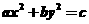 的系数
的系数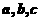 可以从
可以从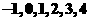 这
这 个数中任取
个数中任取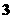 个不同的数而得到,则这样的方程表示焦点在
个不同的数而得到,则这样的方程表示焦点在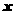 轴上的椭圆的概率是___________.(结果用数值表示)
轴上的椭圆的概率是___________.(结果用数值表示)
2.抛物线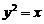 的准线方程是
.
的准线方程是
.
|
定义 |
到定点的距离与到定直线的距离相等的点的轨迹. 说明: 定点在定直线外,定点是轨迹的焦点,定直线是轨迹的准线. |
|
方程 |
1.y2=2px(p≠0),焦点是F(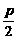 ,0) ,0)2.x2=2py(p≠0),焦点是F(0, 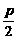 ) ) |
|
性质 |
S:y2=2px(p>0) 1.范围:x≥0 2.对称性:关于x轴对称 3.顶点:原点O 4.准线:x=- 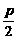 5.通径为 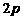 6.抛物线方程中,字母p的几何意义是抛物线的焦点F到准线的距离, 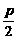 等于焦点到抛物线顶点的距离. 等于焦点到抛物线顶点的距离. |
强化练习
1.已知椭圆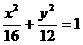 的左焦点是
的左焦点是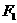 ,右焦点是
,右焦点是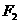 ,点
,点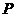 在椭圆上,如果线段
在椭圆上,如果线段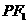 的中点在
的中点在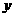 轴上,那么
轴上,那么 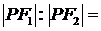 .
.
|
定义 |
到两个定点F1与F2的距离之差的绝对值等于定长(<|F1F2|)的点的轨迹 |
|
方程 |
1. 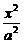 - -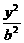 =1,c= =1,c=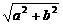 ,焦点是F1(-c,0),F2(c,0) ,焦点是F1(-c,0),F2(c,0)2. 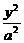 - -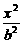 =1,c= =1,c=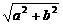 ,焦点是F1(0,-c)、F2(0,c) ,焦点是F1(0,-c)、F2(0,c) |
|
性质 |
H: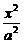 - -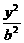 =1(a>0,b>0) =1(a>0,b>0)1.范围:|x|≥a,y∈R 2.对称性:关于x、y轴均对称,关于原点中心对称 3.顶点:轴端点A1(-a,0),A2(a,0) 4.渐近线:y= 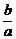 x,y=- x,y=-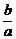 x x |
思考讨论
对于焦点在y轴上的双曲线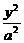 -
-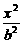 =1(a>0,b>0),其性质如何?
=1(a>0,b>0),其性质如何?
|
定义 |
到两个定点F1、F2的距离之和等于定长(>|F1F2|)的点的轨迹 |
||||
|
1.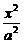 + +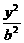 =1(a>b>0),c= =1(a>b>0),c=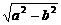 ,焦点是F1(-c,0),F2(c,0) ,焦点是F1(-c,0),F2(c,0)2. 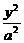 + +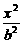 =1(a>b>0),c= =1(a>b>0),c=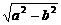 ,焦点是F1(0,-c),F2(0,c) ,焦点是F1(0,-c),F2(0,c)
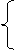 x=acosθ, x=acosθ,
y=bsinθ |
||||
|
性质 |
E: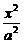 + +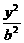 =1(a>b>0) =1(a>b>0)1.范围:|x|≤a,|y|≤b 2.对称性:关于x,y轴均对称,关于原点中心对称 3.顶点:长轴端点A1(-a,0),A2(a,0);短轴端点B1(0,-b),B2(0,b) |
思考讨论
对于焦点在y轴上的椭圆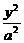 +
+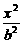 =1(a>b>0),其性质如何?
=1(a>b>0),其性质如何?
15. 求证:等差数列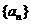 的任意连续m项的和构成的数列
的任意连续m项的和构成的数列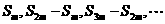 仍为等差数列.
仍为等差数列.
14. 已知数列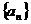 的前
的前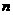 项和
项和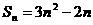 ,求证数列
,求证数列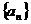 是等差数列,并求其首项、公差、通项公式.
是等差数列,并求其首项、公差、通项公式.
13. 求集合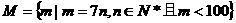 的元素个数,并求这些元素的和.
的元素个数,并求这些元素的和.
12. 成等差数列的四个数之和为26,第二数和第三数之积为40,求这四个数.
11. 求和:1+2+3+…+n=_________________,并推导等差数列{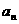 }的前n项和公式
}的前n项和公式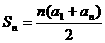 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com