
题目列表(包括答案和解析)
2. 若 (i为虚数单位,
(i为虚数单位, )则
)则 _ .
_ .
1.若集合 ,则
,则 等于_ .
等于_ .
(15)等比数列{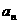 }的前n 项和为
}的前n 项和为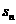 ,已知
,已知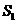 ,
,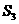 ,
, 成等差数列
成等差数列
(1)求{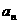 }的公比q;
(2)求
}的公比q;
(2)求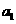 -
-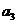 =3,求
=3,求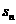 .
.
(16)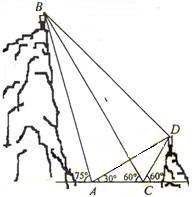 如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为 ,
,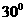 ,于水面C处测得B点和D点的仰角均为
,于水面C处测得B点和D点的仰角均为 ,AC=0.1km。试探究图中B,D间距离与另外哪两点距离相等,然后求B,D的距离(计算结果精确到0.01km,
,AC=0.1km。试探究图中B,D间距离与另外哪两点距离相等,然后求B,D的距离(计算结果精确到0.01km,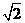
 1.414,
1.414,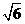
 2.449).
2.449).
(17)某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品。从两个分厂生产的零件中个抽出500件,量其内径尺寸,的结果如下表:
甲厂
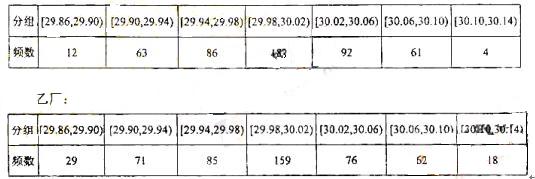
(1) 试分别估计两个分厂生产的零件的优质品率;
(2) 根据以上统计数据填下面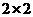 列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
|
|
甲 厂 |
乙 厂 |
合计 |
|
优质品 |
|
|
|
|
非优质品 |
|
|
|
|
合计 |
|
|
|
附: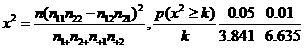 .
.
(18)设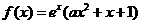 ,且曲线y=f(x)在x=1处的切线与x轴平行.
,且曲线y=f(x)在x=1处的切线与x轴平行.
(I) 求a的值,并讨论f(x)的单调性;
(II) 证明:当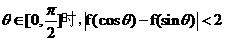 .
.
(19)已知,椭圆C以过点A(1,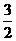 ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。
(1) 求椭圆C的方程;
(2) E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值.
(20)已知函数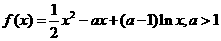 ,
,
(1)讨论函数 的单调性;
的单调性;
(2)证明:若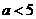 ,则对于任意
,则对于任意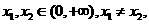 有
有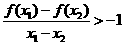 .
.
(1)已知复数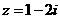 ,那么
,那么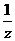 =_________.
=_________.
(2)已知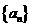 为等差数列,且
为等差数列,且 -2
-2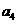 =-1,
=-1, 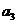 =0,则公差d=_________.
=0,则公差d=_________.
(3) 平面向量a与b的夹角为 ,a=(2,0), | b |=1,则 | a+2b |=_________.
,a=(2,0), | b |=1,则 | a+2b |=_________.
(4)若函数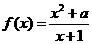 在
在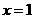 处取极值,则
处取极值,则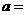 _.
_.
(5)在平面直角坐标系xoy中,四边形ABCD的边AB∥DC,AD∥BC,已知点A(-2,0),B(6,8),C(8,6),则D点的坐标为___________.
 (6) 等差数列
(6) 等差数列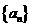 的前n项和为Sn,且
的前n项和为Sn,且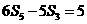 ,则
,则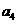 =_________.
=_________.
(7) 已知圆C与直线x-y=0 及x-y-4=0都相切,圆心在直线x+y=0上,则圆C的方程为_________.
(8)ABCD为长方形,AB=2,BC=1,O为AB的中点,在长方形ABCD内随机取一点,取到的点到O的距离大于1的概率为_________.
(9) 已知函数 的图像如图所示,
的图像如图所示,
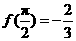 ,则
,则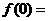 _________.
_________.

(10)已知偶函数 在区间
在区间 单调增加,则满
单调增加,则满
足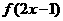 <
< 的x 取值范围是_________.
的x 取值范围是_________.
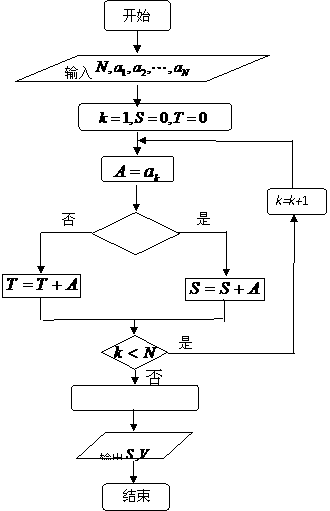
(11)某店一个月的收入和支出总共记录了 N个数据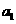 ,
,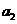 ,。。。
,。。。 ,其中收入记为正数,支出记为负数。该店用右边的程序框图计算月总收入S和月净盈利V,那么在图中空白的判断框和处理框中,应分别填入_____,____.
,其中收入记为正数,支出记为负数。该店用右边的程序框图计算月总收入S和月净盈利V,那么在图中空白的判断框和处理框中,应分别填入_____,____.
(12)已知函数 满足:x≥4,则
满足:x≥4,则 =
=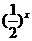 ;当x<4时
;当x<4时 =
=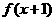 ,则
,则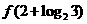 =_________.
=_________.
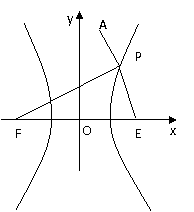 (13)下列4个命题
(13)下列4个命题
 ;
; ㏒1/2x>㏒1/3x;
㏒1/2x>㏒1/3x;
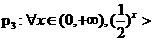 ㏒1/2x ;
㏒1/2x ;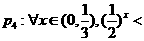 ㏒1/3x ,
㏒1/3x ,
其中的真命题是_________.
(14)已知F是双曲线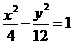 的左焦点,定点A(1,4),P是双曲线右支上的动点,则
的左焦点,定点A(1,4),P是双曲线右支上的动点,则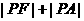 的最小值为_________.
的最小值为_________.
3.(2010江苏卷)13、在锐角三角形ABC,A、B、C的对边分别为a、b、c,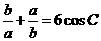 ,则
,则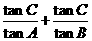 =____▲_____。
=____▲_____。
[解析] 考查三角形中的正、余弦定理三角函数知识的应用,等价转化思想。一题多解。
(方法一)考虑已知条件和所求结论对于角A、B和边a、b具有轮换性。
当A=B或a=b时满足题意,此时有: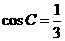 ,
,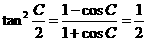 ,
,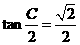 ,
,
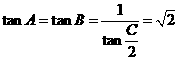 ,
,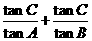 = 4。
= 4。
(方法二)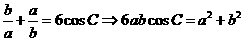 ,
,
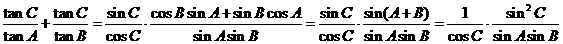
2.(2010江苏卷)10、定义在区间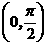 上的函数y=6cosx的图像与y=5tanx的图像的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx的图像交于点P2,则线段P1P2的长为_______▲_____。
上的函数y=6cosx的图像与y=5tanx的图像的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx的图像交于点P2,则线段P1P2的长为_______▲_____。
[解析] 考查三角函数的图象、数形结合思想。线段P1P2的长即为sinx的值,
且其中的x满足6cosx=5tanx,解得sinx=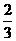 。线段P1P2的长为
。线段P1P2的长为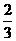
1. (2010福建理数)14.已知函数 和
和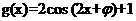 的图象的对称轴完全相同。若
的图象的对称轴完全相同。若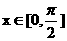 ,则
,则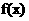 的取值范围是
。
的取值范围是
。
[答案]
[解析]由题意知, ,因为
,因为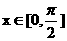 ,所以
,所以 ,由三角函数图象知:
,由三角函数图象知:
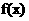 的最小值为
的最小值为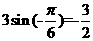 ,最大值为
,最大值为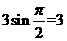 ,所以
,所以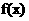 的取值范围是
的取值范围是 。
。
14.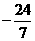 [命题意图]本小题主要考查三角函数值符号的判断、同角三角函数关系、和角的正切公式,同时考查了基本运算能力及等价变换的解题技能.
[命题意图]本小题主要考查三角函数值符号的判断、同角三角函数关系、和角的正切公式,同时考查了基本运算能力及等价变换的解题技能.
[解析]因为 为第二象限的角,又
为第二象限的角,又 , 所以
, 所以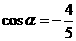 ,
,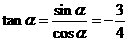 ,所
,所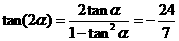
(2010全国卷1理数)(14)已知 为第三象限的角,
为第三象限的角,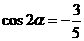 ,则
,则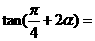 .
.

(2010山东理数)

16.(2010福建文数)观察下列等式:K^S*5U.C#O
① cos2a=2 -1;
-1;
② cos4a=8 - 8
- 8 + 1;
+ 1;
③ cos6a=32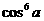 - 48
- 48 + 18
+ 18 - 1;
- 1;
④ cos8a=128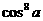 - 256
- 256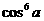 + 160
+ 160 - 32
- 32 + 1;
+ 1;
⑤ cos10a= m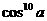 - 1280
- 1280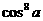 + 1120
+ 1120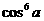 + n
+ n + p
+ p - 1.
- 1.
可以推测,m – n + p = .
[答案]962
[解析]因为
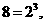
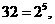
 所以
所以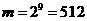 ;观察可得
;观察可得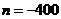 ,
,
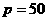 ,所以m – n + p =962。
,所以m – n + p =962。
[命题意图]本小题考查三角变换、类比推理等基础知识,考查同学们的推理能力等。
(2010全国卷1文数)(14)已知 为第二象限的角,
为第二象限的角,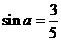 ,则
,则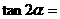 .
.
11.1.解:由A+C=2B及A+ B+ C=180°知,B =60°.由正弦定理知,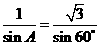 ,即
,即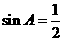 .由
.由 知,
知,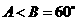 ,则
,则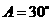 ,
,
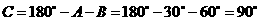 ,
,
(2010广东文数)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com