49、(2010上海文数)20.(本大题满分14分)本题共有2个小题，第1小题满分7分，第2小题满分7分.

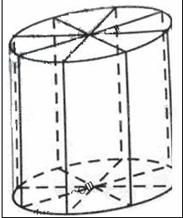
如图所示，为了制作一个圆柱形灯笼，先要制作4个全等的矩形骨架，总计耗用9.6米铁丝，再用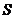平方米塑料片制成圆柱的侧面和下底面(不安装上底面).

(1)当圆柱底面半径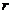取何值时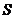，取得最大值？并求出该

最大值(结果精确到0.01平方米);

(2)若要制作一个如图放置的，底面半径为0.3米的灯笼，请作出

用于灯笼的三视图(作图时，不需考虑骨架等因素).

解析：(1) 设圆柱形灯笼的母线长为l，则l=1.2-2r(0<r<0.6)，S=-3p(r-0.4)²+0.48p， 所以当r=0.4时，S取得最大值约为1.51平方米； (2) 当r=0.3时，l=0.6，作三视图略．

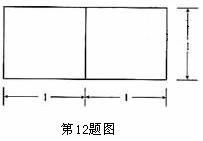
12．若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积等于　　 　　　．

[答案]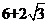

[解析]由正视图知：三棱柱是以底面边长为2，高为1的正三棱柱，所以底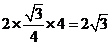面积为

，侧面积为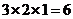，所以其表面积为。

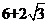[命题意图]本题考查立体几何中的三视图，考查同学们识图的能力、空间想象能力等基本能力。

48、(2010福建理数)

13.[答案]4

[解析]设球半径为r，则由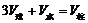可得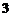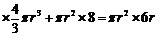,解得r=4.

47、(2010湖北理数)13.圆柱形容器内部盛有高度为8cm的水，若放入三个相同的球(球的半径与圆柱的底面半径相同)后，水恰好淹没最上面的球(如图所示)，则球的半径是　　　　　　 cm。

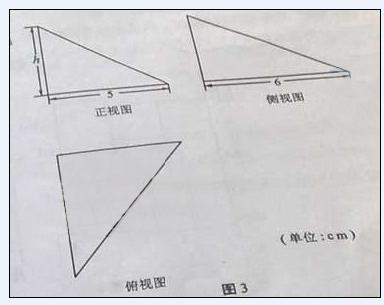
46、(2010湖南理数)13．图3中的三个直角三角形是一个体积为20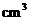的几何体的三视图，则　　　 ．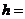

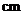45、(2010湖北文数)14.圆柱形容器内盛有高度为3cm的水，若放入三个相同的珠(球的半么与圆柱的底面半径相同)后，水恰好淹没最上面的球(如图所示)，则球的半径是____cm.

[答案]4

[解析]设球半径为r，则由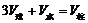可得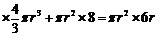,解得r=4.

44、(2010四川文数)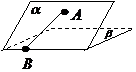(15)如图，二面角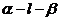的大小是60°，线段.，

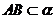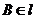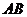与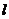所成的角为30°.则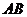与平面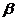所成的角的正弦值是　　　　 .

解析：过点A作平面β的垂线，垂足为C，在β内过C作l的垂线.垂足为D

连结AD，有三垂线定理可知AD⊥l，

故∠ADC为二面角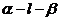的平面角，为60°

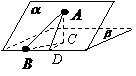又由已知，∠ABD＝30°

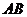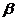连结CB，则∠ABC为与平面所成的角

设AD＝2，则AC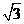＝，CD＝1

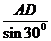AB＝＝4

∴sin∠ABC＝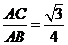

答案：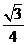

43、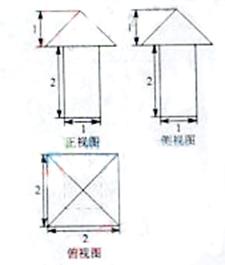(2010天津理数)(12)一个几何体的三视图如图所示，则这个几何体的体积为　　　　　

[答案]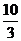

[解析]本题主要考查三视图的概念与柱体、椎体体积的计算，属于容易题。

由三视图可知，该几何体为一个底面边长为1，高为2的正四棱柱与一个底面边长为2，高为1的正四棱锥组成的组合体，因为正巳灵珠的体积为2，正四棱锥的体积为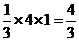，所以该几何体的体积V=2+ =

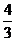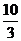
[温馨提示]利用俯视图可以看出几何体底面的形状，结合正视图与侧视图便可得到几何体的形状，求锥体体积时不要丢掉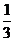哦。

42、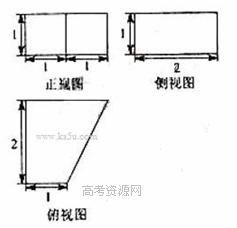(2010天津文数)(12)一个几何体的三视图如图所示，则这个几何体的体积为　　　　　 。

[答案]3

[解析]本题主要考查三视图的基础知识，和主题体积的计算，属于容易题。

由俯视图可知该几何体的底面为直角梯形，则正视图和俯视图可知该几何体的高为1，结合三个试图可知该几何体是底面为直角梯形的直四棱柱，所以该几何题的体积为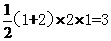

[温馨提示]正视图和侧视图的高是几何体的高，由俯视图可以确定几何体底面的形状，本题也可以将几何体看作是底面是长为3，宽为2，高为1的长方体的一半。