
题目列表(包括答案和解析)
3、(2010浙江理数)(4)设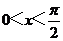 ,则“
,则“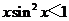 ”是“
”是“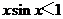 ”的
”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
解析:因为0<x<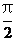 ,所以sinx<1,故xsin2x<xsinx,结合xsin2x与xsinx的取值范围相同,可知答案选B,本题主要考察了必要条件、充分条件与充要条件的意义,以及转化思想和处理不等关系的能力,属中档题
,所以sinx<1,故xsin2x<xsinx,结合xsin2x与xsinx的取值范围相同,可知答案选B,本题主要考察了必要条件、充分条件与充要条件的意义,以及转化思想和处理不等关系的能力,属中档题
2、(2010浙江理数)(9)设函数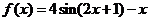 ,则在下列区间中函数
,则在下列区间中函数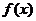 不存在零点的是
不存在零点的是
(A)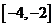 (B)
(B)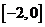 (C)
(C)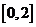 (D)
(D)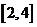
解析:将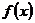 的零点转化为函数
的零点转化为函数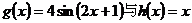 的交点,数形结合可知答案选A,本题主要考察了三角函数图像的平移和函数与方程的相关知识点,突出了对转化思想和数形结合思想的考察,对能力要求较高,属较难题
的交点,数形结合可知答案选A,本题主要考察了三角函数图像的平移和函数与方程的相关知识点,突出了对转化思想和数形结合思想的考察,对能力要求较高,属较难题
7.(2010湖南文数)在△ABC中,角A,B,C所对的边长分别为a,b,c,若∠C=120°,c=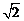 a,则
a,则
A.a>b B.a<b
C. a=b D.a与b的大小关系不能确定
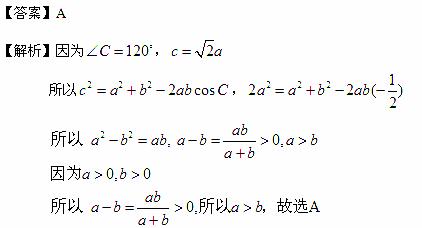
[命题意图]本题考查余弦定理,特殊角的三角函数值,不等式的性质,比较法,属中档题。
1、(2010上海文数)18.若△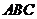 的三个内角满足
的三个内角满足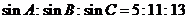 ,则△
,则△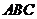
(A)一定是锐角三角形. (B)一定是直角三角形.
(C)一定是钝角三角形. (D)可能是锐角三角形,也可能是钝角三角形.
解析:由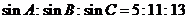 及正弦定理得a:b:c=5:11:13
及正弦定理得a:b:c=5:11:13
由余弦定理得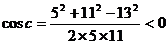 ,所以角C为钝角
,所以角C为钝角
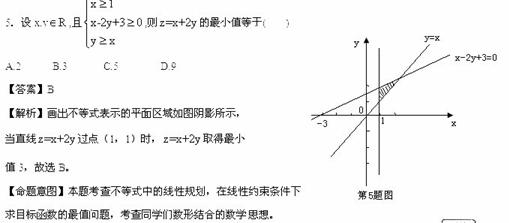
8.(2010福建理数)设不等式组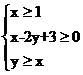 所表示的平面区域是
所表示的平面区域是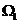 ,平面区域是
,平面区域是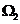 与
与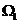 关于直线
关于直线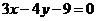 对称,对于
对称,对于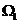 中的任意一点A与
中的任意一点A与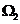 中的任意一点B,
中的任意一点B, 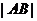 的最小值等于( )
的最小值等于( )
A.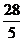 B.4 C.
B.4 C.
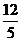 D.2
D.2
[答案]B
[解析]由题意知,所求的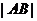 的最小值,即为区域
的最小值,即为区域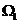 中的点到直线
中的点到直线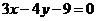 的距离的最小值的两倍,画出已知不等式表示的平面区域,如图所示,
的距离的最小值的两倍,画出已知不等式表示的平面区域,如图所示,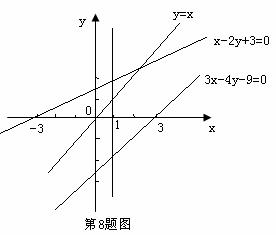
可看出点(1,1)到直线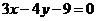 的距离最小,故
的距离最小,故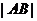 的最小值为
的最小值为
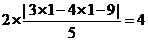 ,所以选B。
,所以选B。
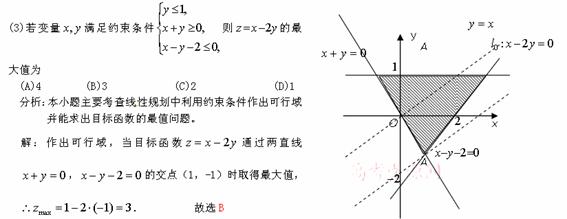
3.B [命题意图]本小题主要考查线性规划知识、作图、识图能力及计算能力.
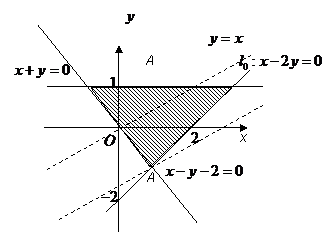 [解析]画出可行域(如右图),
[解析]画出可行域(如右图),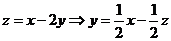 ,由图可知,当直线
,由图可知,当直线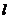 经过点A(1,-1)时,z最大,且最大值为
经过点A(1,-1)时,z最大,且最大值为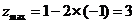 .
.

(2010全国卷1理数)(8)设a=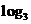 2,b=ln2,c=
2,b=ln2,c=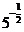 ,则
,则
(A) a<b<c (B)b<c<a (C) c<a<b (D) c<b<a

(2010全国卷1理数)
(2010四川文数)(11)设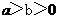 ,则
,则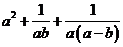 的最小值是
的最小值是
(A)1 (B)2 (C)3 (D)4
解析: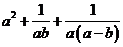


 w_w w. k#s5_
w_w w. k#s5_
=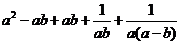
=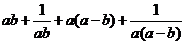
≥2+2=4
当且仅当ab=1,a(a-b)=1时等号成立
如取a=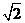 ,b=
,b=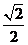 满足条件.
满足条件.
答案:D
(2010四川文数)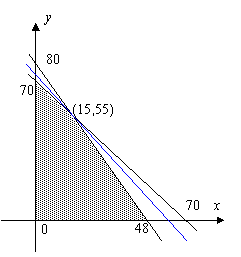 (8)某加工厂用某原料由车间加工出
(8)某加工厂用某原料由车间加工出 产品,由乙车间加工出
产品,由乙车间加工出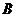 产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克
产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克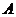 产品,每千克
产品,每千克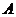 产品获利40元.乙车间加工一箱原料需耗费工时6小时可加工出4千克
产品获利40元.乙车间加工一箱原料需耗费工时6小时可加工出4千克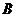 产品,每千克
产品,每千克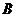 产品获利50元.甲、乙两车间每天功能完成至多70多箱原料的加工,每天甲、乙车间耗费工时总和不得超过480小时,甲、乙两车间每天获利最大的生产计划为
产品获利50元.甲、乙两车间每天功能完成至多70多箱原料的加工,每天甲、乙车间耗费工时总和不得超过480小时,甲、乙两车间每天获利最大的生产计划为

 w_w w. k#s5_
w_w w. k#s5_
(A)甲车间加工原料10箱,乙车间加工原料60箱
(B)甲车间加工原料15箱,乙车间加工原料55箱
(C)甲车间加工原料18箱,乙车间加工原料50箱
(D)甲车间加工原料40箱,乙车间加工原料30箱高^考#资*源^网
解析:解析:设甲车间加工原料x箱,乙车间加工原料y箱
则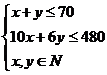
目标函数z=280x+300y
结合图象可得:当x=15,y=55时z最大
本题也可以将答案逐项代入检验.
答案:B

 w_w w. k#s5_
w_w w. k#s5_
(2010山东理数)
10.C [命题意图]本小题以指数、对数为载体,主要考查指数函数与对数函数的性质、实数大小的比较、换底公式、不等式中的倒数法则的应用.
[解析1]
a=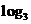 2=
2=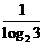 , b=In2=
, b=In2=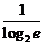 ,而
,而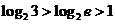 ,所以a<b,
,所以a<b,
c=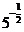 =
=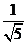 ,而
,而 ,所以c<a,综上c<a<b.
,所以c<a,综上c<a<b.
[解析2]a=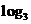 2=
2=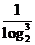 ,b=ln2=
,b=ln2=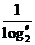 ,
, 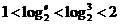 ,
,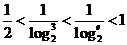 ; c=
; c=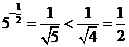 ,∴c<a<b
,∴c<a<b
(2010全国卷1文数)(3)若变量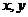 满足约束条件
满足约束条件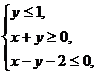 则
则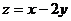 的最大值为
的最大值为
(A)4 (B)3 (C)2 (D)1
8.C
[解析]不等式表示的区域是一个三角形,3个顶点是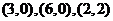 ,目标函数
,目标函数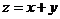 在
在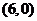 取最大值6。
取最大值6。
[规律总结]线性规划问题首先作出可行域,若为封闭区域(即几条直线围成的区域)则区域端点的值是目标函数取得最大或最小值,求出直线交点坐标代入目标函数即可求出最大值.
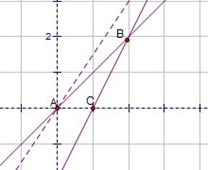 (2010重庆文数)(7)设变量
(2010重庆文数)(7)设变量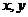 满足约束条件
满足约束条件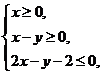 则
则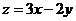 的最大值为
的最大值为
(A)0 (B)2
(C)4 (D)6
解析:不等式组表示的平面区域如图所示,
当直线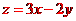 过点B时,在y轴上截距最小,z最大
过点B时,在y轴上截距最小,z最大
由B(2,2)知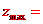 4
4

解析:将最大值转化为y轴上的截距,可知答案选A,本题主要考察了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题
 (2010重庆理数)(7)已知x>0,y>0,x+2y+2xy=8,则x+2y的最小值是
(2010重庆理数)(7)已知x>0,y>0,x+2y+2xy=8,则x+2y的最小值是
A. 3 B.
4 C. D.
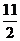
解析:考察均值不等式
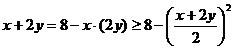 ,整理得
,整理得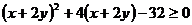
即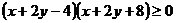 ,又
,又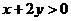 ,
,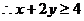
 (2010重庆理数)(4)设变量x,y满足约束条件
(2010重庆理数)(4)设变量x,y满足约束条件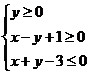 ,则z=2x+y的最大值为
,则z=2x+y的最大值为
A.-2 B. 4 C. 6 D. 8
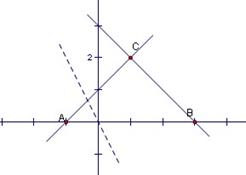
解析:不等式组表示的平面区域如图所示
当直线过点B(3,0)的时候,z取得最大值6
(2010北京理数)(7)设不等式组 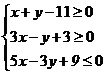 表示的平面区域为D,若指数函数y=
表示的平面区域为D,若指数函数y=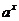 的图像上存在区域D上的点,则a 的取值范围是
的图像上存在区域D上的点,则a 的取值范围是
(A)(1,3]
(B )[2,3] (C )
(1,2]
(D )[ 3, 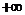 ]
]
答案:A
(2010四川理数)(12)设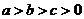 ,则
,则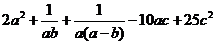 的最小值是
的最小值是

 w_w w. k#s5_
w_w w. k#s5_
(A)2 (B)4 (C) 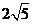 (D)5
(D)5
解析: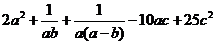
=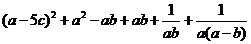 w_w_w.k*s 5*
w_w_w.k*s 5*
=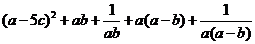
≥0+2+2=4
当且仅当a-5c=0,ab=1,a(a-b)=1时等号成立
如取a=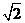 ,b=
,b=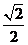 ,c=
,c=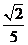 满足条件.
满足条件.
答案:B
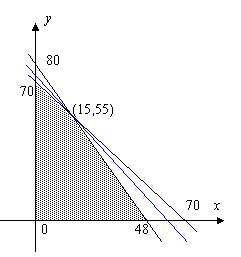 (2010四川理数)(7)某加工厂用某原料由甲车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A产品,每千克A产品获利40元,乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙两车间耗费工时总和不得超过480小时,甲、乙两车间每天总获利最大的生产计划为w_w_w.k*s 5*
(2010四川理数)(7)某加工厂用某原料由甲车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A产品,每千克A产品获利40元,乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙两车间耗费工时总和不得超过480小时,甲、乙两车间每天总获利最大的生产计划为w_w_w.k*s 5*
(A)甲车间加工原料10箱,乙车间加工原料60箱
(B)甲车间加工原料15箱,乙车间加工原料55箱
(C)甲车间加工原料18箱,乙车间加工原料50箱
(D)甲车间加工原料40箱,乙车间加工原料30箱
解析:设甲车间加工原料x箱,乙车间加工原料y箱
则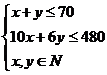


 w_w w. k#s5_
w_w w. k#s5_
目标函数z=280x+300y
结合图象可得:当x=15,y=55时z最大
本题也可以将答案逐项代入检验.
答案:B w_w_w.k*s 5*
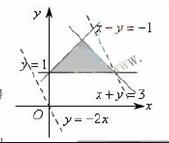 (2010天津文数)(2)设变量x,y满足约束条件
(2010天津文数)(2)设变量x,y满足约束条件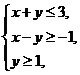 则目标函数z=4x+2y的最大值为
则目标函数z=4x+2y的最大值为
(A)12 (B)10 (C)8 (D)2
[答案]B
[解析]本题主要考查目标函数最值的求法,属于容易题,做出可行域,如图由图可知,当目标函数过直线y=1与x+y=3的交点(2,1)时z取得最大值10.
(2010福建文数)
(2010全国卷1文数)(10)设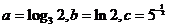 则
则
(A)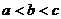 (B)
(B)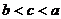 (C)
(C) 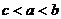 (D)
(D) 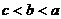
3.(2010江西理数)不等式 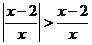 高☆考♂资♀源*网的解集是( )
高☆考♂资♀源*网的解集是( )
A. 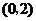 B.
B. 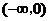 C.
C. 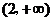 D.
D. 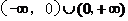
[答案] A
[解析]考查绝对值不等式的化简.绝对值大于本身,值为负数.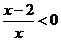 ,解得A。
,解得A。
或者选择x=1和x=-1,两个检验进行排除。
(2010安徽文数)(8)设x,y满足约束条件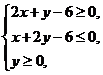 则目标函数z=x+y的最大值是
则目标函数z=x+y的最大值是
(A)3 (B) 4 (C) 6 (D)8
1.[答案]D
[解析]观察图形可知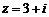 ,则
,则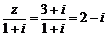 ,即对应点H(2,-1),故D正确.
,即对应点H(2,-1),故D正确.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com