
题目列表(包括答案和解析)
11 已知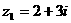 ,
,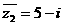 ,那么
,那么 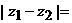 _______________
_______________
12 若定义在区间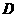 上的函数
上的函数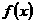 对于
对于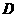 上的任意
上的任意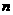 个值
个值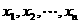 总满足,
总满足,
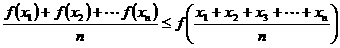 则称
则称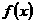 为
为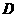 上的凸函数,现已知
上的凸函数,现已知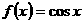 在(0,
在(0,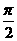 )上是凸函数,则在锐角
)上是凸函数,则在锐角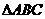 中,
中,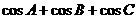 的最大值是_______________
的最大值是_______________
13 实数x y满足不等式组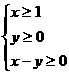 ,则W=
,则W=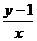 的取值范围是_____________
的取值范围是_____________
14 已知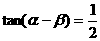 ,
,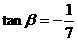 ,且
,且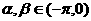 ,则
,则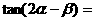 __________,
__________,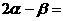 _________
_________
17(本题满分12分)
已知函数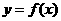 的图象关于直线
的图象关于直线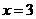 对称,当
对称,当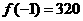 且
且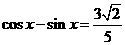 时,求
时,求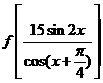 的值
的值
18(本题满分12分)
某种工作元件有3个,它能正常工作的概率均为0.6,请设计成一个工作系统,使该系统正常工作的概率不低于07(要求画出系统图,并计算正常工作的概率)
19(本题满分12分)
设函数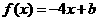 ,不等式
,不等式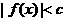 的解集为(-1,2)
的解集为(-1,2)
(Ⅰ)判断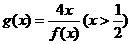 的单调性,并用定义证明;
的单调性,并用定义证明;
(Ⅱ)解不等式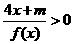
20(本题满分12分)
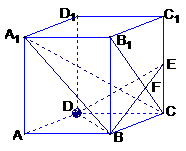
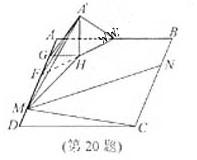
如图,在直三棱柱ABC-A1B1C1中,AC=BC=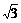 ,AA1=1,∠ACB=90°
,AA1=1,∠ACB=90°
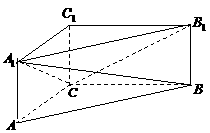 (Ⅰ)求异面直线A1B与CB1所成角的大小;
(Ⅰ)求异面直线A1B与CB1所成角的大小;
(Ⅱ)问:在A1B1边上是否存在一点Q,使
得平面QBC与平面A1BC所成的角为30°,若存在,请求点Q的位置,若不存在,请说明理由
21(本题满分12分)
设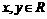 ,
,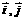 为直角坐标平面内x轴y轴正方向上的单位向量,若
为直角坐标平面内x轴y轴正方向上的单位向量,若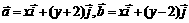 ,且
,且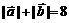
(Ⅰ)求动点M(x,y)的轨迹C的方程;
(Ⅱ)设曲线C上两点AB,满足(1)直线AB过点(0,3),(2)若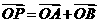 ,则OAPB为矩形,试求AB方程
,则OAPB为矩形,试求AB方程
22(本题满分14分)
直线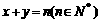 与x轴y 轴所围成区域内部(不包括边界)的整点个数为
与x轴y 轴所围成区域内部(不包括边界)的整点个数为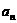 ,所围成区域内部(包括边界)的整点个数为
,所围成区域内部(包括边界)的整点个数为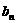 ,(整点就是横坐标,纵坐标都为整数的点)
,(整点就是横坐标,纵坐标都为整数的点)
(Ⅰ)求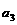 和
和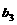 的值;
的值;
(Ⅱ)求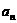 及
及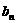 的表达式;
的表达式;
(Ⅲ)对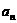 个整点用红黄蓝白四色之一着色,其方法总 数为An,对
个整点用红黄蓝白四色之一着色,其方法总 数为An,对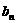 个整点用红黄两色之一着色,其方法总数为Bn,试比较An与Bn的大小
个整点用红黄两色之一着色,其方法总数为Bn,试比较An与Bn的大小
13在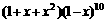 的展开式中,含
的展开式中,含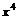 的系数为
的系数为
14若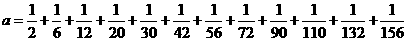 ,且
,且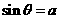 ,
,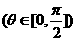 ,则
,则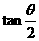 =
=
15一个公司有N个员工,下设一些部门,现采用分层抽样方法从全体员工中抽取一个容量为n的样本(N是n的倍数),已知某部门被抽取m个员工,那么这个部门的员工数为
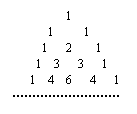 16如右图,在杨辉三角形中,从上往下数共有n(n∈N*)行,在这些数中非1的数字之和为
16如右图,在杨辉三角形中,从上往下数共有n(n∈N*)行,在这些数中非1的数字之和为
1已知集合AB,全集∪,给出下列四个命题
⑴若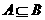 ,则
,则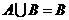 ; ⑵若
; ⑵若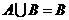 ,则
,则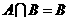 ;
;
⑶若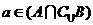 ,则
,则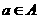 ; ⑷若
; ⑷若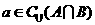 ,则
,则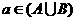
则上述正确命题的个数为
A1 B2 C3 D4
2设非零向量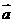
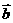
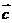 ,若
,若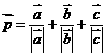 ,那么
,那么 的取值范围为
的取值范围为
A[0,1] B[0,2] C[0,3] D[1,2]
3设等差数列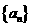 的前
的前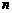 项和为
项和为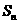 ,当
,当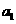
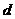 变化时,若
变化时,若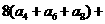
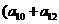
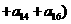 是一个定值,那么下列各数中也为定值的是
是一个定值,那么下列各数中也为定值的是
A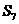 B
B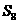 C
C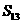 D
D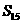
4设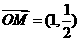 ,
,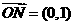 ,则满足条件
,则满足条件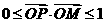 ,
,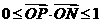 的动点P的变化范围(图中阴影部分含边界)是
的动点P的变化范围(图中阴影部分含边界)是
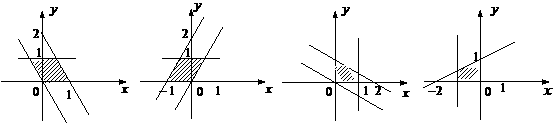
A B C D
5在斜三角形ABC中, 且
且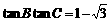 ,则∠A的值为
,则∠A的值为
A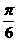 B
B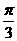 C
C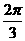 D
D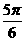
6设两个非零向量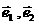 不共线,若
不共线,若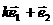 与
与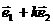 也不共线,则实数k的取值范围为
也不共线,则实数k的取值范围为
A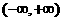 B
B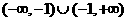
C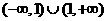 D
D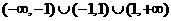
7设ABCD是半径为2的球面上四个不同的点,且满足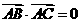 ,
,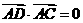 ,
,
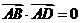 ,则
,则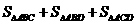 的最大值为
的最大值为
A16 B8 C4 D2
8由方程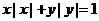 确定的函数
确定的函数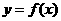 在R上是
在R上是
A奇函数 B偶函数 C增函数 D减函数
9已知函数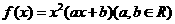 在
在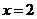 时有极值,其图象在点
时有极值,其图象在点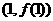 处的切线与直线
处的切线与直线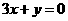 平行,则函数
平行,则函数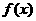 的单调减区间为
的单调减区间为
A(-∞,0) B(0,2) C(2,+∞) D(-∞,+∞)
10定义在R上的函数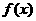 对任意的x都有
对任意的x都有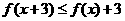 和
和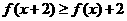 且
且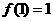 ,则
,则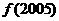 的值为
的值为
A2002 B2003 C2004 D2005
11分别把写有0,1,2,3,4数字的四张纸片放入一盒中,每次取一张记数字为m,放回后再取一张记数字为n,设P(m,n)为平面中的点,则点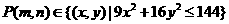 的概率为
的概率为
A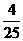 B
B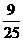 C
C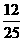 D
D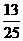
12下列三图中的多边形均为正多边形,M,N是所在边的中点,双曲线均以图中的F1,F2为焦点,设图示①②③中的双曲线的离心率分别为e1,e2,e3
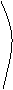
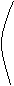
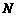
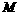
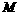
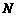

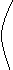

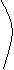
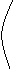


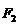
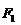
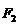
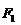
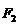

① ② ③
则e1e2e3的大小关系为
Ae1>e2>e3 Be1<e2<e3 Ce2= e3 <e1 De1= e3>e2
17 本题满分12分)
已知在⊿ABC中,角A B C的对边为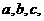 ,向量
,向量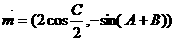 ,
,
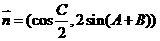 ,
, ⊥
⊥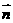
(1)求角C
(2)若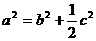 ,试求
,试求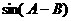 的值
的值
18 (本题满分12分)
粒子A位于数轴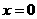 处,粒子B位于
处,粒子B位于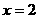 处,这两粒子每隔1秒向左或向右移动一个单位,设向右移动的概率为
处,这两粒子每隔1秒向左或向右移动一个单位,设向右移动的概率为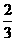 ,向左移的概率为
,向左移的概率为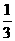
(1)求第三秒时,粒子A在点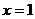 处的概率
处的概率
(2)求第2秒时,粒子A B同在点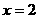 处的概率
处的概率
 19 (本题满分12分)
19 (本题满分12分)
已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1=4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F,
(1)求证:A1C⊥平面BED;
(2)求A1B与平面BDE所成角的正弦值
20 (本题满分12分)已知函数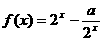
(1)将函数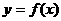 的图象向右平移两个单位,得到函数
的图象向右平移两个单位,得到函数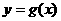 ,求
,求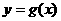 的解析式 (2)函数
的解析式 (2)函数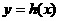 与函数
与函数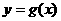 的图象关于直线
的图象关于直线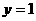 对称,求
对称,求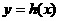 的解析式;(3)设
的解析式;(3)设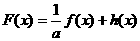 ,
,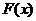 的最小值是
的最小值是 ,且
,且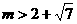 求实数
求实数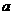 的取值范围
的取值范围
21 (本题满分12分)
自点A(0,-1)向抛物线C: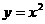 作切线AB,切点为B,且B在第一象限,再过线段AB的中点M作直线
作切线AB,切点为B,且B在第一象限,再过线段AB的中点M作直线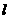 与抛物线C交于不同的两点E、F 直线AF AE分别交抛物线C于P、Q两点
与抛物线C交于不同的两点E、F 直线AF AE分别交抛物线C于P、Q两点
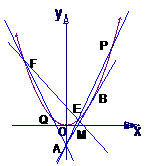 (1)求切线AB的方程及切点B的坐标
(1)求切线AB的方程及切点B的坐标
(2)证明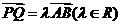
22 (本题满分14分)由原点O向三次曲线
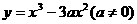 引切线,切点为P1
引切线,切点为P1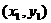 (O,P1两点不重合),再由P1引此曲线的切线,切于点P2
(O,P1两点不重合),再由P1引此曲线的切线,切于点P2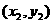 (P1,P2不重合),如此继续下去,得到点列:
(P1,P2不重合),如此继续下去,得到点列: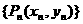
(1)求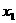 ;
;
(2)求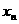 与
与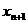 满足的关系式;
满足的关系式;
(3)若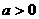 ,试判断
,试判断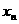 与
与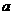 的大小关系,并说明理由
的大小关系,并说明理由
13 已知函数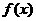 是R上的减函数,A(0,--3),B(--2,3)是其图象上的两点,那么不等式
是R上的减函数,A(0,--3),B(--2,3)是其图象上的两点,那么不等式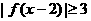 的解集是______________
的解集是______________
14 从4名男生和2名女生中任选3人参加演讲比赛,则所选3人中至少有1名女生的概率是______
15 双曲线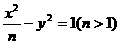 的两个焦点为F1,F2,P在双曲线上,且满足|PF1|+|PF2|=
的两个焦点为F1,F2,P在双曲线上,且满足|PF1|+|PF2|=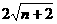 ,则⊿PF1F2的面积为____________
,则⊿PF1F2的面积为____________
16 有一个正四棱锥,它的底面边长和侧棱长均为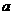 ,现在要用一张正方形的包装纸将它完全包住 (不能裁剪纸,但可以折叠)那么包装纸的最小边长应为__________________
,现在要用一张正方形的包装纸将它完全包住 (不能裁剪纸,但可以折叠)那么包装纸的最小边长应为__________________
1 已知集合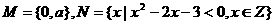 ,若
,若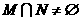 ,则
,则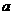 的值为
的值为
A 1 B 2 C 1或2 D 不为零的任意实数
2 下列函数中周期是2的函数是( )
A 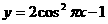 B
B 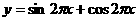
C 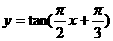 D
D 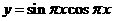
3 下列命题中正确的是( )
A 若直线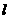 ∥平面M,则直线
∥平面M,则直线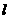 的垂线必平行于平面M;
的垂线必平行于平面M;
B 若直线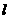 与平面M相交,则有且只有一个平面经过
与平面M相交,则有且只有一个平面经过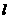 且与平面M垂直;
且与平面M垂直;
C 若直线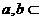 平面M,
平面M,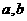 相交,且直线
相交,且直线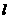 ⊥
⊥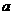 ,
,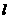 ⊥
⊥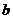 ,则
,则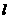 ⊥M;
⊥M;
D 若直线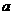 ∥平面M,直线
∥平面M,直线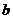 ⊥
⊥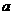 ,则
,则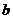 ⊥M
⊥M
4 已知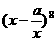 展开式中常数项为1120,其中实数
展开式中常数项为1120,其中实数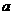 是常数,则展开式中各项系数的和为( )
是常数,则展开式中各项系数的和为( )
A 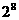 B
B 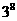 C 1或
C 1或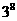 D 1或
D 1或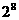
5 若函数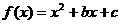 的图象的顶点在第四象限,则函数
的图象的顶点在第四象限,则函数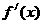 的图象是( )
的图象是( )
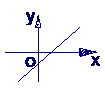
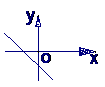
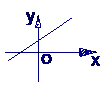
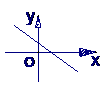
A B C D
6 已知实数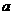 满足
满足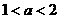
命题P:函数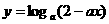 在区间[0,1]上是减函数
在区间[0,1]上是减函数
命题Q: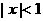 是
是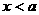 的充分不必要条件 则(
)
的充分不必要条件 则(
)
A “P或Q”为真命题; B “P且Q”为假命题;
C “┐P且Q”为真命题; D “┐P或┐Q”为真命题
7 已知两个点M(--5,0)和N(5,0),若直线上存在点P,使|PM|--|PN|=6,则称该直线为“B型直线”
给出下列直线①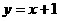 ;②
;②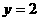 ;③
;③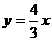 ;④
;④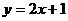 其中为“B型直线”的是( )
其中为“B型直线”的是( )
A ①③ B ①② C ③④ D ①④
8 在数列{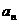 }中,
}中,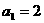 ,
,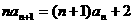 (
(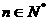 ),则
),则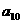 为( )
为( )
A 34 B 36 C 38 D 40
9 已知点B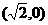 ,点O为坐标原点,点A在圆
,点O为坐标原点,点A在圆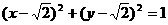 上,则向量
上,则向量
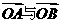 的夹角
的夹角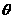 的最大值与最小值分别为( )
的最大值与最小值分别为( )
A 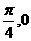 B
B 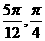 C
C 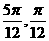 D
D 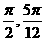
10 设函数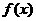 为定义域在R上的以3为周期的奇函数,若
为定义域在R上的以3为周期的奇函数,若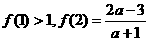 ,则
,则
A 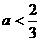 B
B 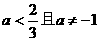 C
C 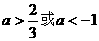 D
D 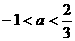
11 某商场宣传在“五一黄金周”期间对顾客购物实行一定的优惠,商场规定:
①如一次性购物不超过200元,不予以折扣;
②如一次性购物超过200元但不超过500元的,按标价给予九折优惠;
③如一次性购物超过500元的,其中500元给予9折优惠,超过500元的部分给予八五折优惠 某人两次去购物,分别付款176元和432元,如果他只去一次购买同样的商品,则应付款( )
A 608元 B 574 1元 C 582 6元 D 456 8元
12 已知直线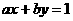 (
(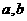 不全为0)与圆
不全为0)与圆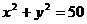 的公共点,且公共点的横 纵坐标均为整数,那么这样的直线共有( )
的公共点,且公共点的横 纵坐标均为整数,那么这样的直线共有( )
A 66条 B 72条 C 74条 D 78条
3.(2010全国卷2) (19)如图,直三棱柱
(19)如图,直三棱柱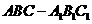 中,
中,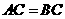 ,
,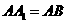 ,
,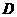 为
为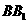 的中点,
的中点,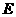 为
为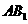 上的一点,
上的一点,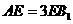 .
.
(Ⅰ)证明: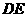 为异面直线
为异面直线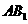 与
与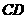 的公垂线;
的公垂线;
(Ⅱ)设异面直线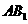 与
与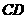 的夹角为45°,求二面角
的夹角为45°,求二面角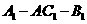 的大小.
的大小.
[命题意图]本试题主要考查空间的线面关系与空间角的求解,考查考生的空间想象与推理计算的能力.
2. (2010浙江理)(20)(本题满分15分)如图, 在矩形
(2010浙江理)(20)(本题满分15分)如图, 在矩形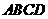 中,点
中,点 分别在线段
分别在线段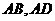 上,
上,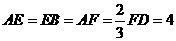 .沿直线
.沿直线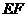 将
将
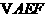 翻折成
翻折成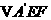 ,使平面
,使平面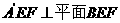 .
.
(Ⅰ)求二面角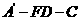 的余弦值;
的余弦值;
(Ⅱ)点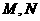 分别在线段
分别在线段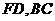 上,若沿直线
上,若沿直线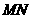 将四边形
将四边形 向上翻折,使
向上翻折,使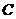 与
与 重合,求线段
重合,求线段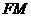 的长。
的长。
解析:本题主要考察空间点、线、面位置关系,二面角等基础知识,空间向量的应用,同事考查空间想象能力和运算求解能力。
 (Ⅰ)解:取线段EF的中点H,连结
(Ⅰ)解:取线段EF的中点H,连结 ,因为
,因为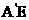 =
=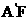 及H是EF的中点,所以
及H是EF的中点,所以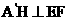 ,
,
又因为平面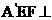 平面
平面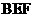 .
.
如图建立空间直角坐标系A-xyz
则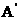 (2,2,
(2,2,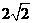 ),C(10,8,0),
),C(10,8,0),
F(4,0,0),D(10,0,0).
故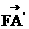 =(-2,2,2
=(-2,2,2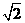 ),
),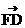 =(6,0,0).
=(6,0,0).
设 =(x,y,z)为平面
=(x,y,z)为平面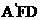 的一个法向量,
的一个法向量,
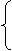 -2x+2y+2
-2x+2y+2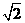 z=0
z=0
所以
6x=0.
取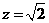 ,则
,则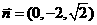 。
。
又平面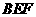 的一个法向量
的一个法向量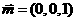 ,
,
故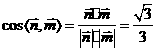 。
。
所以二面角的余弦值为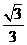
(Ⅱ)解:设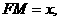 则
则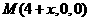 ,
,
因为翻折后,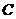 与
与 重合,所以
重合,所以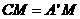 ,
,
故,
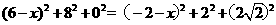 ,得
,得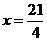 ,
,
经检验,此时点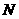 在线段
在线段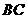 上,
上,
所以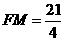 。
。
 方法二:
方法二:
(Ⅰ)解:取线段 的中点
的中点 ,
, 的中点
的中点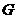 ,连结
,连结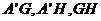 。
。
因为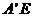 =
=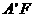 及
及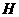 是
是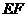 的中点,
的中点,
所以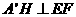
又因为平面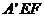
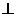 平面
平面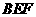 ,
,
所以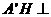 平面
平面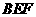 ,
,
又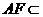 平面
平面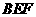 ,
,
故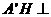
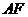 ,
,
又因为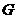 、
、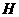 是
是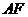 、
、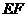 的中点,
的中点,
易知 ∥
∥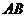 ,
,
所以
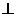
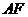 ,
,
于是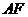
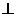 面
面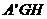 ,
,
所以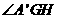 为二面角
为二面角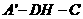 的平面角,
的平面角,
在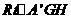 中,
中,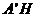 =
=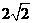 ,
, =2,
=2,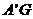 =
=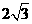
所以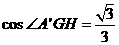 .
.
故二面角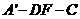 的余弦值为
的余弦值为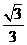 。
。
(Ⅱ)解:设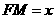 ,
,
因为翻折后,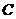 与
与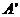 重合,
重合,
所以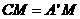 ,
,
而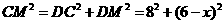 ,
,
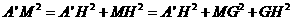
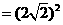
得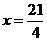 ,
,
经检验,此时点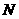 在线段
在线段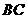 上,
上,
所以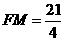 。
。
1.(2010湖南文)18.(本小题满分12分)
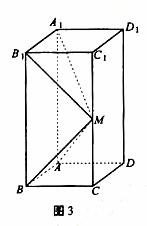 如图所示,在长方体
如图所示,在长方体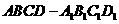 中,AB=AD=1,AA1=2,M是棱CC1的中点
中,AB=AD=1,AA1=2,M是棱CC1的中点
(Ⅰ)求异面直线A1M和C1D1所成的角的正切值;
(Ⅱ)证明:平面ABM⊥平面A1B1M1

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com