
题目列表(包括答案和解析)
4.(全国Ⅰ新卷文9)设偶函数f(x)满足f(x)=2x-4 (x 0),则
0),则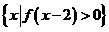 =
=
(A)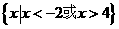 (B)
(B)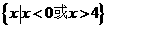
(C)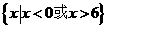 (D)
(D)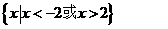
[答案]B
解析:当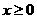 时,
时,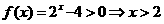 ,又由于函数是偶函数,所以
,又由于函数是偶函数,所以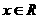 时,
时,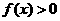 的解集为
的解集为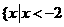 或
或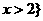 ,故
,故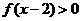 的解集为
的解集为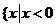 或
或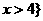 .
.
另解:根据已知条件和指数函数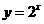 的图像易知
的图像易知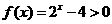 的解集为
的解集为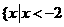 或
或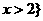 ,故
,故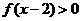 的解集为
的解集为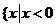 或
或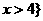 .
.
3.(全国Ⅰ新卷理8)设偶函数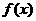 满足
满足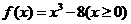 ,则
,则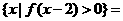
(A) 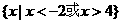 (B)
(B) 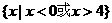
(C) 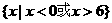 (D)
(D) 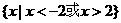
[答案]B
解析:当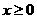 时,
时,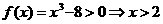 ,又由于函数是偶函数,所以
,又由于函数是偶函数,所以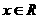 时,
时,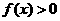 的解集为
的解集为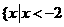 或
或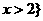 ,故
,故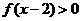 的解集为
的解集为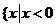 或
或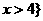 .
.
另解:根据已知条件和幂函数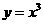 的图像易知
的图像易知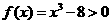 的解集为
的解集为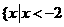 或
或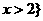 ,故
,故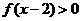 的解集为
的解集为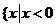 或
或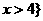 .
.
2.(江西卷文5)不等式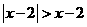 的解集是
的解集是
A.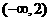 B.
B.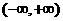 C.
C.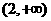 D.
D.
[答案]A
[解析]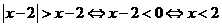
[命题意图]考查含绝对值不等式的解法,对于含绝对值不等式主要是去掉绝对值后再求解,可以通过绝对值的意义、零点分区间法、平方等方法去掉绝对值。
但此题利用代值法会更好
1.(江西卷理3)不等式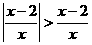 的解集是
的解集是
A.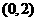 B.
B.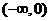 C.
C.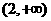 D.
D.
[答案] A
[解析]考查绝对值不等式的化简.绝对值大于本身,值为负数.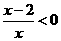 ,解得A。
,解得A。
或者选择x=1和x=-1,两个检验进行排除。
15 (本小题满分13分)
解不等式: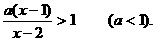
16 (本小题满分13分)
已知 ,
,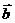 都是非零向量,且
都是非零向量,且 +3
+3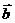 与7
与7 -5
-5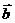 垂直,
垂直, -4
-4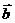 与7
与7 -2
-2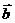 垂直,求
垂直,求 与
与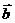 的夹角
的夹角
17 (本小题满分13分)
甲乙两人独立解某一道数学题,已知该题被甲独立解出的概率为0 6,被甲或乙解出的概率为0 92
(1)求该题被乙独立解出的概率;
(2)求解出该题的人数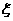 的数学期望和方差
的数学期望和方差
18 (本小题满分13分)
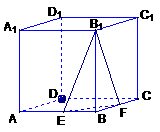 在正方体
在正方体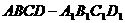 中,
中,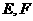 分别是
分别是 的中点,试问在棱
的中点,试问在棱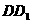 上能否找到一点
上能否找到一点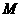 ,使
,使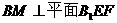 ?若能,确定点
?若能,确定点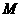 的位置;若不能,说明理由
的位置;若不能,说明理由
19 (本小题满分14分)
设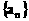 为公差大于0的等差数列,
为公差大于0的等差数列,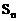 为数列
为数列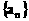 的前n项的和 已知
的前n项的和 已知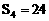 ,
,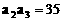
(1) 求数列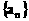 的通项公式
的通项公式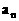 ;
;
(2) 若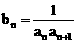 ,求
,求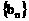 的前n项和
的前n项和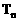
(3)求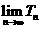 的值
的值
20 (本小题满分14分)
设抛物线过定点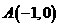 ,且以直线
,且以直线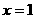 为准线
为准线
(Ⅰ)求抛物线顶点的轨迹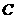 的方程;
的方程;
(Ⅱ)若直线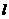 与轨迹
与轨迹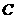 交于不同的两点
交于不同的两点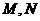 ,且线段
,且线段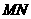 恰被直线
恰被直线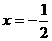 平分,设弦MN的垂直平分线的方程为
平分,设弦MN的垂直平分线的方程为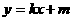 ,试求
,试求 的取值范围
的取值范围
11 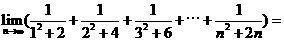 ;
;
12 已知m, l是直线,α β γ是平面,给出下列命题:
① β∩γ=l, l//α,m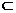 α, m⊥γ, 则α⊥γ且m//β;
α, m⊥γ, 则α⊥γ且m//β;
② 若l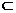 β且l⊥α,则α⊥β;
β且l⊥α,则α⊥β;
③ 若β∩γ=l, l//α, m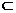 α和m⊥γ,则α⊥γ且l⊥m;
α和m⊥γ,则α⊥γ且l⊥m;
④ 若m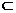 α, l
α, l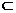 β, 且α//β,则m//l;
β, 且α//β,则m//l;
⑤ 若m//α, m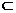 β, α∩β=l,则m⊥l,
β, α∩β=l,则m⊥l,
其中所有正确命题的序号是
13 设直线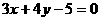 的倾斜角为
的倾斜角为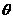 ,则该直线关于直线
,则该直线关于直线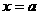 (
(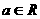 )对称的直线的倾斜角为
)对称的直线的倾斜角为
14 使函数y=f ( x ) 图象上每一点的纵坐标保持不变, 横坐标缩小到原来的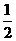 ,然后再将其图象沿x轴向左平移
,然后再将其图象沿x轴向左平移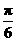 个单位, 得到的曲线与y=sin2x相同
则f ( x ) 的表达式为
个单位, 得到的曲线与y=sin2x相同
则f ( x ) 的表达式为
1 在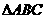 中,
中,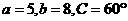 ,则
,则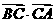 的值为 ( )
的值为 ( )
A 20
B 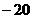 C
C 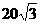 D
D 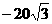
2 复数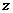 满足
满足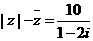 ,则
,则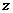 等于( )
等于( )
(A)3+4i (B)-3-4i (C)3-4i (D)-3+4i
3 已知函数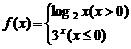 则
则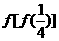 的值为( )
的值为( )
(A)9
(B)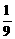 (C)-9 (D)
(C)-9 (D)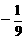
4 若0<a<1,则函数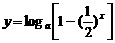 在定义域上是( )
在定义域上是( )
(A)增函数且y>0 (B)增函数且y<0
(C)减函数且y>0 (D)减函数且y<0
5 已知长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为4,则点A1到截面AB1D1的距离是( )
(A)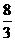 (B)
(B)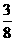 (C)
(C)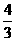 (D)
(D)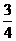
6 若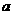 b∈R,且
b∈R,且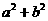 =10,则
=10,则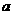 -b的取值范围是( )
-b的取值范围是( )
(A)[0,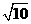 ]
(B)[0,2
]
(B)[0,2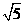 ]
]
(C)[-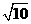 ,
,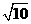 ] (D)[-2
] (D)[-2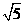 ,2
,2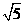 ]
]
7 抛物线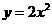 和
和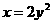 的焦点之间的距离为( )
的焦点之间的距离为( )
(A) 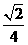 (B)
(B)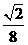 (C)
(C)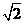 (D)
(D)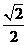
8 点P是曲线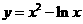 上任意一点,则点P到直线
上任意一点,则点P到直线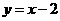 的最小距离为 ( )
的最小距离为 ( )
A 1 B 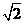 C
C 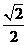 D
D 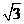
9 数列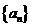 中,
中,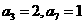 ,又数列
,又数列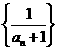 是等差数列,则
是等差数列,则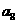 =( )
=( )
(A)0
(B)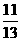 (C)
(C)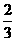 (D)-1
(D)-1
10 设双曲线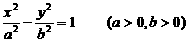 中,离心率
中,离心率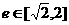 ,则两条渐近线所成的角θ(以实轴为角平分线)的取值范围是( )
,则两条渐近线所成的角θ(以实轴为角平分线)的取值范围是( )
A 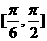 B
B 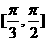 C
C 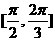 D
D 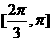
20. (本小题满分14分)
若F1 F2为双曲线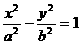 的左 右焦点,O为坐标原点,P
的左 右焦点,O为坐标原点,P
在双曲线左支上,M在右准线上,且满足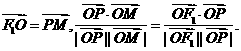
(1)求此双曲线的离心率;
(2)若此双曲线过点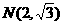 ,求双曲线方程;
,求双曲线方程;
(3)设(2)中双曲线的虚轴端点为B1,B2(B1在y轴正半轴上),求B2作直线AB与双曲线交于A B两点,求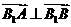 时,直线AB的方程
时,直线AB的方程
19. (本题满分14分)
已知数列{an}的前n项和为Sn,且满足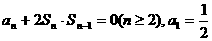
(1)求证:{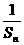 }是等差数列;(2)求an的表达式;
}是等差数列;(2)求an的表达式;
(3)若bn=2(1-n)·an(n≥2)时,求证:b22+b32+…+bn2<1
18. (本题满分13分)
已知函数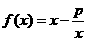 (x>1)
(x>1)
(1)若函数在f(x)上是增函数,求实数p的取值范围;
(2)解关于x的不等式f(x)<2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com