
题目列表(包括答案和解析)
1.(上海卷理11文14)将直线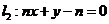 、
、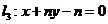 (
(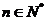 ,
,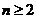 )x轴、y轴围成的封闭图形的面积记为
)x轴、y轴围成的封闭图形的面积记为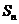 ,则
,则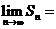 。
。
解析:B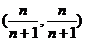 所以BO⊥AC,
所以BO⊥AC,
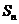 =
=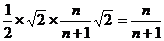 所以
所以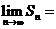
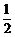
4. (重庆卷理21)在数列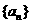 中,
中,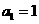 ,
,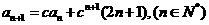 其中实数
其中实数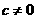 .
.
(Ⅰ) 求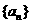 的通项公式;
的通项公式;
(Ⅱ) 若对一切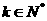 有
有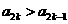 ,求c的取值范围.
,求c的取值范围.


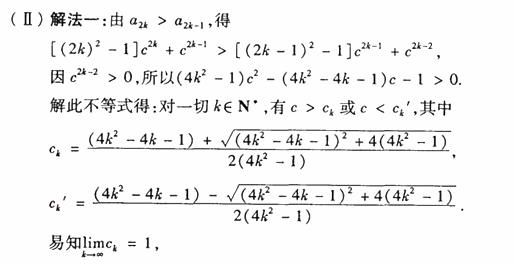


3.(全国Ⅰ卷理22)已知数列 中,
中,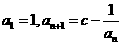 .
.
(Ⅰ)设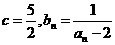 ,求数列
,求数列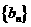 的通项公式;
的通项公式;
(Ⅱ)求使不等式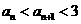 成立的
成立的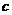 的取值范围 .
的取值范围 .
[命题意图]本小题主要考查数列的通项公式、等比数列的定义、递推数列、不等式等基础知识和基本技能,同时考查分析、归纳、探究和推理论证问题的能力,在解题过程中也渗透了对函数与方程思想、化归与转化思想的考查.
[解析]

(Ⅱ)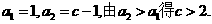
用数学归纳法证明:当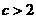 时
时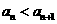 .
.
(ⅰ)当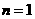 时,
时, ,命题成立;
,命题成立;
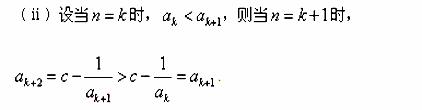

2.(湖北卷理20)已知数列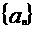 满足:
满足: 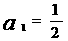 ,
, 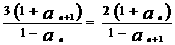 ,
,
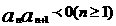 ;数列
;数列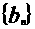 满足:
满足: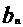 =
=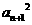 -
-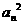 (n≥1).
(n≥1).
(Ⅰ)求数列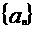 ,
,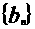 的通项公式;
的通项公式;
(Ⅱ)证明:数列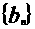 中的任意三项不可能成等差数列.
中的任意三项不可能成等差数列.


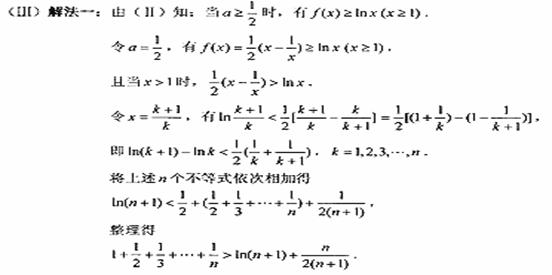

1.(安徽卷理20)设数列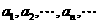 中的每一项都不为0。证明:
中的每一项都不为0。证明: 为等差数列的充分必要条件是:对任何
为等差数列的充分必要条件是:对任何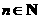 ,都有
,都有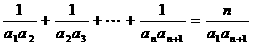 。
。




2.(浙江卷理14)设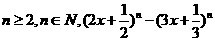
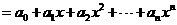 ,将
,将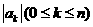 的最小值记为
的最小值记为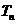 ,则
,则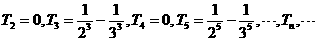
其中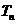 =__________________
.
=__________________
.
[答案]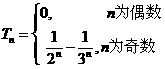
解析:本题主要考察了合情推理,利用归纳和类比进行简单的推理,属容易题
1.(福建卷文16)观察下列等式:
① cos2α=2 cos2 α-1;
② cos 4α=8 cos4 α-8 cos2 α+1;
③ cos 6α=32 cos6 α-48 cos4 α+18 cos2 α-1;
④ cos 8α= 128 cos8α-256cos6 α+160 cos4 α-32 cos2 α+1;
⑤ cos 10α=mcos10α-1280 cos8α+1120cos6 α+ncos4 α+p cos2 α-1;
可以推测,m-n+p= .
[答案]962
[解析]因为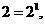
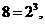
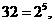
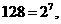 所以
所以 ;观察可得
;观察可得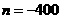 ,
,
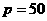 ,所以m – n + p
=962。
,所以m – n + p
=962。
[命题意图]本小题考查三角变换、类比推理等基础知识,考查同学们的推理能力等。
22.(全国Ⅱ卷理22)设函数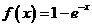 .
.
(Ⅰ)证明:当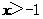 时,
时,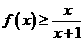 ;
;
(Ⅱ)设当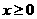 时,
时,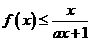 ,求a的取值范围.
,求a的取值范围.
[命题意图]本题主要考查导数的应用和利用导数证明不等式,考查考生综合运用知识的能力及分类讨论的思想,考查考生的计算能力及分析问题、解决问题的能力.
21.(全国Ⅰ新卷文21)设函数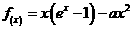
(Ⅰ)若a=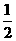 ,求
,求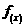 的单调区间;
的单调区间;
(Ⅱ)若当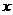 ≥0时
≥0时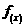 ≥0,求a的取值范围
≥0,求a的取值范围
解:(Ⅰ)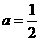 时,
时,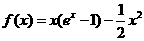 ,
,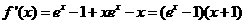 。当
。当 时
时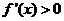 ;当
;当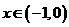 时,
时,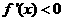 ;当
;当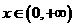 时,
时,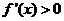 。故
。故 在
在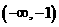 ,
,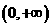 单调增加,在(-1,0)单调减少。
单调增加,在(-1,0)单调减少。
(Ⅱ)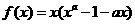 。令
。令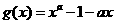 ,则
,则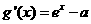 。若
。若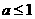 ,则当
,则当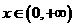 时,
时,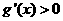 ,
, 为减函数,而
为减函数,而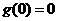 ,从而当x≥0时
,从而当x≥0时 ≥0,即
≥0,即 ≥0.若
≥0.若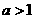 ,则当
,则当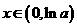 时,
时,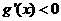 ,
, 为减函数,而
为减函数,而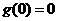 ,从而当
,从而当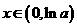 时
时 <0,即
<0,即 <0. 综合得
<0. 综合得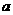 的取值范围为
的取值范围为
20.(全国Ⅰ新卷理21)设函数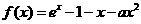 。
。
若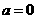 ,求
,求 的单调区间;
的单调区间;
若当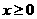 时
时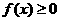 ,求
,求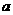 的取值范围
的取值范围
解:(1)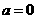 时,
时,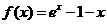 ,
,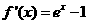 .
.
当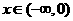 时,
时,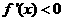 ;当
;当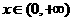 时,
时,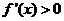 .故
.故 在
在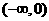 单调减少,在
单调减少,在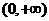 单调增加
单调增加
(II)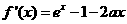
由(I)知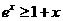 ,当且仅当
,当且仅当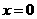 时等号成立.故
时等号成立.故
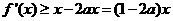 ,
,
从而当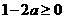 ,即
,即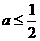 时,
时,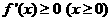 ,而
,而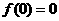 ,
,
于是当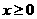 时,
时,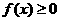 .
.
由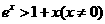 可得
可得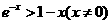 .从而当
.从而当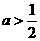 时,
时,
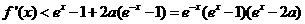 ,
,
故当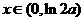 时,
时,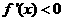 ,而
,而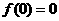 ,于是当
,于是当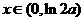 时,
时,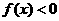 .
.
综合得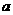 的取值范围为
的取值范围为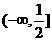 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com