
题目列表(包括答案和解析)
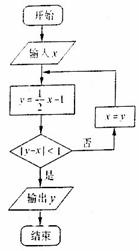
8.(山东卷理13)执行右图所示的程序框图,若输入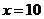 ,则输出
,则输出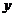 的值为
。
的值为
。
[答案]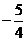
[解析]当x=10时,y=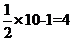 ,此时|y-x|=6;
,此时|y-x|=6;
当x=4时,y=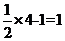 ,此时|y-x|=3;当x=1时,y=
,此时|y-x|=3;当x=1时,y=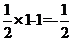 ,此时|y-x|=
,此时|y-x|=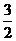 ;
;
当x=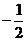 时,y=
时,y=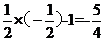 ,此时|y-x|=
,此时|y-x|=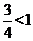 ,故输出y的值为
,故输出y的值为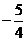 。
。
 [命题意图]本题考查程序框图的基础知识,考查了同学们的试图能力。
[命题意图]本题考查程序框图的基础知识,考查了同学们的试图能力。
7.(江苏卷7)右图是一个算法的流程图,则输出S的值是__▲
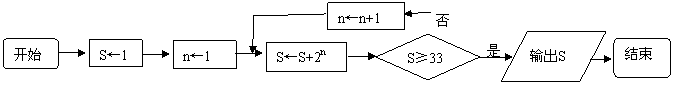
 [答案]63
[答案]63
[解析]考查流程图理解。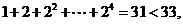 输出
输出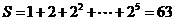 。
。
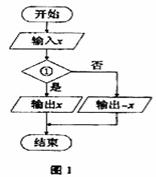
6.(湖南卷文12).图1是求实数x的绝对值的算法程序框图,则判断框①中可填
[答案]
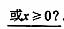
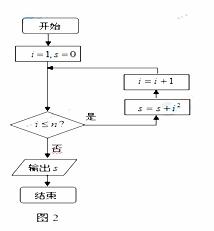 第五(
第五(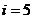 )步:
)步: ,输出
,输出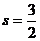
5.(湖南卷理12)图2是求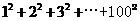 的值的程序框图,则正整数
的值的程序框图,则正整数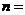 .
.

[考题分类]
(三)解答题(共6题)
1.(北京卷理20)已知集合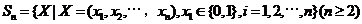 对于错误!不能通过编辑域代码创建对象。,
对于错误!不能通过编辑域代码创建对象。,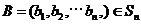 ,定义A与B的差为错误!不能通过编辑域代码创建对象。A与B之间的距离为
,定义A与B的差为错误!不能通过编辑域代码创建对象。A与B之间的距离为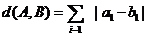
(Ⅰ)证明:错误!不能通过编辑域代码创建对象。,且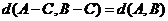 ;
;
(Ⅱ)证明:错误!不能通过编辑域代码创建对象。三个数中至少有一个是偶数
(Ⅲ) 设P错误!不能通过编辑域代码创建对象。,P中有m(m≥2)个元素,记P中所有两元素间距离的平均值为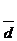 (P).
(P).
证明:错误!不能通过编辑域代码创建对象。(P)≤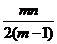 .
.
证明:(I)设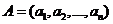 ,
,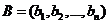 ,
,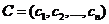
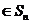
因为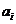 ,
,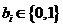 ,所以
,所以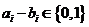 ,
,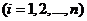 www.@ks@
www.@ks@
从而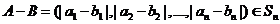
又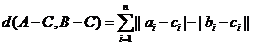
由题意知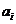 ,
,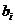 ,
,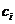
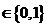
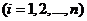 .
.
当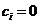 时,
时,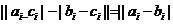 ;
;
当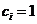 时,
时,
所以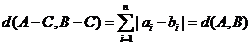
(II)设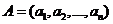 ,
,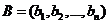 ,
,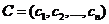
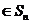
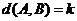 ,
,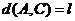 ,
,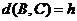 .
.
记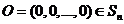 ,由(I)可知
,由(I)可知

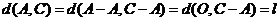
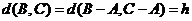
所以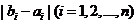 中1的个数为
中1的个数为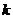 ,
,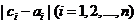 的1的个数为
的1的个数为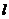 。
。
设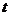 是使
是使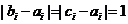 成立的
成立的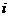 的个数,则
的个数,则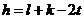
由此可知,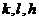 三个数不可能都是奇数,
三个数不可能都是奇数,
即 ,
,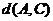 ,
,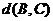 三个数中至少有一个是偶数。
三个数中至少有一个是偶数。
(III)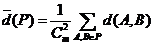 ,其中
,其中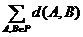 表示
表示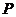 中所有两个元素间距离的总和,www.@ks@
中所有两个元素间距离的总和,www.@ks@
设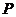 种所有元素的第
种所有元素的第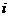 个位置的数字中共有
个位置的数字中共有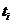 个1,
个1,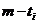 个0则
个0则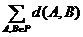 =
=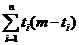
由于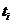
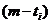
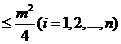 所以
所以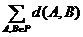
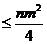
从而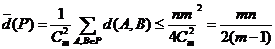
2. (北京卷文20)已知集合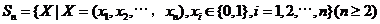 对于
对于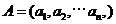 ,
,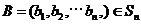 ,定义A与B的差为
,定义A与B的差为
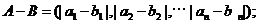
A与B之间的距离为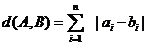
(Ⅰ)当n=5时,设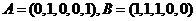 ,求
,求 ,
, ;
;
(Ⅱ)证明: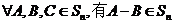 ,且
,且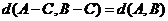 ;
;
(Ⅲ) 证明: 三个数中至少有一个是偶数
三个数中至少有一个是偶数
(Ⅰ)解: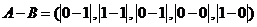 =(1,0,1,0,1)
=(1,0,1,0,1)

 设
设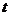 是使
是使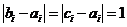 成立的
成立的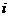 的个数。则
的个数。则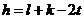
3.(广东卷理21))设A(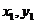 ),B(
),B(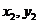 )是平面直角坐标系xOy上的两点,先定义由点A到点B的一种折线距离ρ(A,B)为ρ(A,B)=
)是平面直角坐标系xOy上的两点,先定义由点A到点B的一种折线距离ρ(A,B)为ρ(A,B)= +
+ .对于平面
.对于平面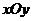 上给定的不同的两点A(
上给定的不同的两点A(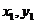 ),B(
),B(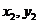 )
)
若点C(x, y)是平面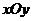 上的点,试证明ρ
上的点,试证明ρ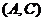 +ρ
+ρ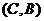
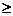 ρ
ρ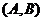 ;
;
在平面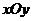 上是否存在点C(x, y),同时满足①ρ
上是否存在点C(x, y),同时满足①ρ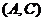 +ρ
+ρ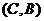 =
ρ
=
ρ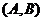 ;
②ρ
;
②ρ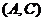 =
ρ
=
ρ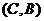 ;若存在,请求所给出所有符合条件的点;若不存在,请予以证明。
;若存在,请求所给出所有符合条件的点;若不存在,请予以证明。
解析:设A(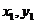 ),B(错误!不能通过编辑域代码创建对象。)是平面直角坐标系xOy上的两点,先定义由点A到点B的一种折线距离p(A,B)为
),B(错误!不能通过编辑域代码创建对象。)是平面直角坐标系xOy上的两点,先定义由点A到点B的一种折线距离p(A,B)为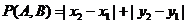 .
.

当且仅当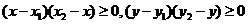 时等号成立,即
时等号成立,即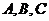 三点共线时等号成立.
三点共线时等号成立.
(2)当点C(x, y) 同时满足①P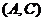 +P错误!不能通过编辑域代码创建对象。=
P
+P错误!不能通过编辑域代码创建对象。=
P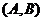 ,②P错误!不能通过编辑域代码创建对象。= P
,②P错误!不能通过编辑域代码创建对象。= P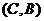 时,点
时,点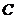 是线段
是线段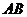 的中点.
的中点. 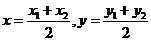 ,即存在点
,即存在点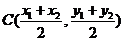 满足条件。
满足条件。
4.(江苏卷23)已知△ABC的三边长为有理数
(1)求证cosA是有理数
(2)对任意正整数n,求证cosnA也是有理数
[解析] 本题主要考查余弦定理、数学归纳法等基础知识,考查推理论证的能力与分析问题、解决问题的能力。满分10分。
(方法一)(1)证明:设三边长分别为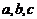 ,
,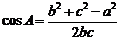 ,∵
,∵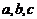 是有理数,
是有理数,
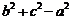 是有理数,分母
是有理数,分母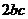 为正有理数,又有理数集对于除法的具有封闭性,
为正有理数,又有理数集对于除法的具有封闭性,
∴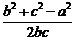 必为有理数,∴cosA是有理数。
必为有理数,∴cosA是有理数。
(2)①当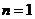 时,显然cosA是有理数;
时,显然cosA是有理数;
当 时,∵
时,∵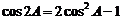 ,因为cosA是有理数, ∴
,因为cosA是有理数, ∴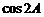 也是有理数;
也是有理数;
②假设当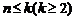 时,结论成立,即coskA、
时,结论成立,即coskA、 均是有理数。
均是有理数。
当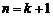 时,
时,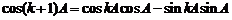 ,
,
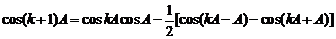 ,
,
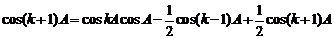 ,
,
解得: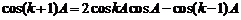
∵cosA,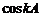 ,
, 均是有理数,∴
均是有理数,∴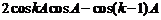 是有理数,
是有理数,
∴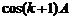 是有理数。 即当
是有理数。 即当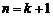 时,结论成立。
时,结论成立。
综上所述,对于任意正整数n,cosnA是有理数。
(方法二)证明:(1)由AB、BC、AC为有理数及余弦定理知
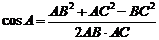 是有理数。
是有理数。
(2)用数学归纳法证明cosnA和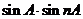 都是有理数。
都是有理数。
①当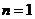 时,由(1)知
时,由(1)知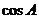 是有理数,从而有
是有理数,从而有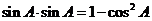 也是有理数。
也是有理数。
②假设当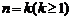 时,
时,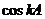 和
和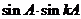 都是有理数。
都是有理数。
当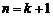 时,由
时,由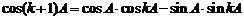 ,
,
 ,
,
及①和归纳假设,知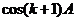 和
和 都是有理数。
都是有理数。
即当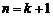 时,结论成立。
时,结论成立。
综合①、②可知,对任意正整数n,cosnA是有理数。
5.(上海卷理22)若实数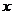 、
、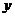 、
、 满足
满足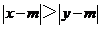 ,则称
,则称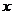 比
比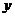 远离
远离 .
.
(1)若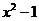 比1远离0,求
比1远离0,求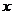 的取值范围;
的取值范围;
(2)对任意两个不相等的正数 、
、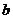 ,证明:
,证明: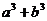 比
比 远离
远离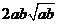 ;
;
(3)已知函数 的定义域
的定义域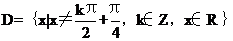 .任取
.任取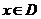 ,
, 等于
等于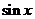 和
和 中远离0的那个值.写出函数
中远离0的那个值.写出函数 的解析式,并指出它的基本性质(结论不要求证明).
的解析式,并指出它的基本性质(结论不要求证明).
解析:(1) 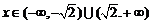 ;
(2) 对任意两个不相等的正数a、b,有
;
(2) 对任意两个不相等的正数a、b,有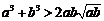 ,
,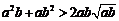 ,
因为
,
因为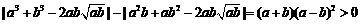 ,
所以
,
所以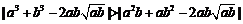 ,即a3+b3比a2b+ab2远离
,即a3+b3比a2b+ab2远离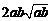 ;
(3)
;
(3) 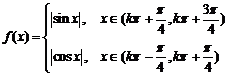 ,
性质:1°f(x)是偶函数,图像关于y轴对称,2°f(x)是周期函数,最小正周期
,
性质:1°f(x)是偶函数,图像关于y轴对称,2°f(x)是周期函数,最小正周期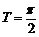 ,
3°函数f(x)在区间
,
3°函数f(x)在区间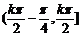 单调递增,在区间
单调递增,在区间 单调递减,kÎZ,
4°函数f(x)的值域为
单调递减,kÎZ,
4°函数f(x)的值域为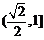 .
.
6.(上海卷文22)若实数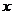 、
、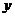 、
、 满足
满足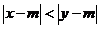 ,则称
,则称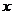 比
比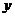 接近
接近 .
.
(1)若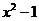 比3接近0,求
比3接近0,求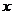 的取值范围;
的取值范围;
(2)对任意两个不相等的正数 、
、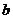 ,证明:
,证明: 比
比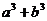 接近
接近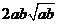 ;
;
(3)已知函数 的定义域
的定义域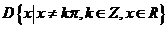 .任取
.任取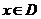 ,
, 等于
等于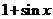 和
和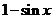 中接近0的那个值.写出函数
中接近0的那个值.写出函数 的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明).
的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明).
解析:(1) xÎ(-2,2);
(2) 对任意两个不相等的正数a、b,有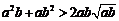 ,
,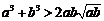 ,
因为
,
因为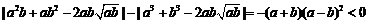 ,
所以
,
所以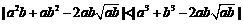 ,即a2b+ab2比a3+b3接近
,即a2b+ab2比a3+b3接近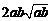 ;
(3)
;
(3) 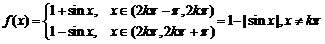 ,kÎZ,
f(x)是偶函数,f(x)是周期函数,最小正周期T=p,函数f(x)的最小值为0,
函数f(x)在区间
,kÎZ,
f(x)是偶函数,f(x)是周期函数,最小正周期T=p,函数f(x)的最小值为0,
函数f(x)在区间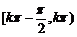 单调递增,在区间
单调递增,在区间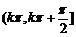 单调递减,kÎZ.
单调递减,kÎZ.
(一)选择题(共5 题)
1.(福建卷理10)对于具有相同定义域 的函数
的函数 和
和 ,若存在函数
,若存在函数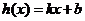 (
(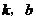 为常数),对任给的正数
为常数),对任给的正数 ,存在相应的
,存在相应的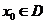 ,使得当
,使得当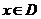 且
且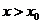 时,总有
时,总有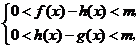 则称直线
则称直线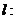
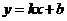 为曲线
为曲线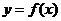 与
与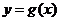 的“分渐近线”。给出定义域均为D=
的“分渐近线”。给出定义域均为D= 的四组函数如下:
的四组函数如下:
①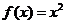 ,
,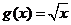 ;②
;②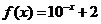 ,
,
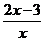 ;
;
③
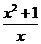 ,
,
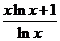 ;④
;④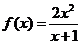 ,
, 。
。
其中,曲线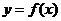 与
与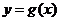 存在“分渐近线”的是
存在“分渐近线”的是
A.①④ B.②③ C.②④ D.③④
[答案]C
[解析]要透过现象看本质,存在分渐近线的充要条件是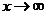 时,
时,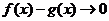 。对于1,当
。对于1,当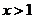 时便不符合,所以1不存在;对于2,肯定存在分渐近线,因为当时,
时便不符合,所以1不存在;对于2,肯定存在分渐近线,因为当时,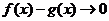 ;对于3,
;对于3, ,设
,设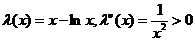 且
且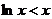 ,所以当
,所以当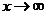 时
时 越来愈大,从而
越来愈大,从而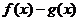 会越来越小,不会趋近于0,所以不存在分渐近线;4当
会越来越小,不会趋近于0,所以不存在分渐近线;4当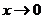 时,
时,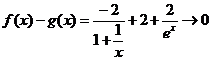 ,因此存在分渐近线。故,存在分渐近线的是24选C
,因此存在分渐近线。故,存在分渐近线的是24选C
[命题意图]本题从大学数列极限定义的角度出发,仿造构造了分渐近线函数,目的是考查学生分析问题、解决问题的能力,考生需要抓住本质:存在分渐近线的充要条件是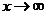 时,
时,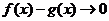 进行做答,是一道好题,思维灵活。
进行做答,是一道好题,思维灵活。
2.(广东卷文10)在集合{a,b,c,d}上定义两种运算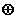 和
和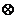 如下:
如下:

 w_w w. k#s5_
w_w w. k#s5_

那么d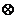
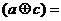
A.a B.b C.c D.d
解:由上表可知: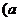 +
+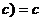 ,故
,故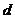 *
*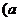 +
+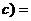
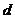 *
*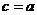 ,选A。
,选A。
3.(湖北卷理10文10)记实数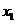 ,
,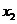 ,……
,……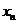 中的最大数为max
中的最大数为max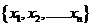 ,最小数为min
,最小数为min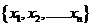 。已知ABC的三边长位a,b,c(
。已知ABC的三边长位a,b,c(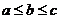 ),定义它的亲倾斜度为
),定义它的亲倾斜度为
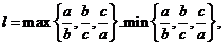 则“
则“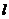 =1”是“
=1”是“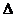 ABC为等边三角形”的
ABC为等边三角形”的
A.必要而不充分的条件 B.充分而不必要的条件
C.充要条件 D.既不充分也不必要条件
[答案]A
[解析]若△ABC为等边三角形时,即a=b=c,则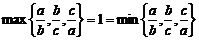 则l=1;若△ABC为等腰三角形,如a=2,b=2,c=3时,
则l=1;若△ABC为等腰三角形,如a=2,b=2,c=3时,
则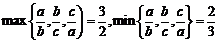 ,此时l=1仍成立但△ABC不为等边三角形,所以A正确.
,此时l=1仍成立但△ABC不为等边三角形,所以A正确.
4.(山东卷理12文12)定义平面向量之间的一种运算“⊙”如下,对任意的a=(m,u),b=(p,q),另a⊙b=mq-np,下面的说法错误的是
(A)若a与b共线,则a⊙b=0
(B)a⊙b=b⊙a
(C)对任意的λ∈R,有(λa)⊙b=λ(a⊙b)
(D)(a⊙b)2+(a·b)2=|a|2 |b|2
[答案]B
[解析]若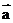 与
与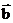 共线,则有
共线,则有 ,故A正确;因为
,故A正确;因为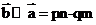 ,而
,而
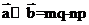 ,所以有
,所以有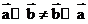 ,故选项B错误,故选B。
,故选项B错误,故选B。
[命题意图]本题在平面向量的基础上,加以创新,属创新题型,考查平面向量的基础知识以及分析问题、解决问题的能力。
5.(浙江卷理10)设函数的集合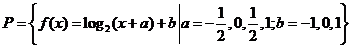 ,
,
平面上点的集合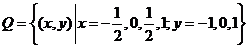 ,则在同一直角坐标系中,
,则在同一直角坐标系中,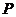 中函数
中函数 的图象恰好经过
的图象恰好经过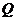 中两个点的函数的个数是
中两个点的函数的个数是
(A)4 (B)6 (C)8 (D)10
解析:当a=0,b=0;a=0,b=1;a=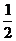 ,b=0;
a=
,b=0;
a=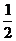 ,b=1;a=1,b=-1;a=1,b=1时满足题意,故答案选B,本题主要考察了函数的概念、定义域、值域、图像和对数函数的相关知识点,对数学素养有较高要求,体现了对能力的考察,属中档题
,b=1;a=1,b=-1;a=1,b=1时满足题意,故答案选B,本题主要考察了函数的概念、定义域、值域、图像和对数函数的相关知识点,对数学素养有较高要求,体现了对能力的考察,属中档题
 (二)填空题(共5题)
(二)填空题(共5题)
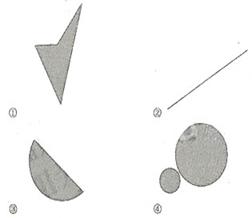
1.(福建卷文15)对于平面上的点集Ω,如果连接Ω中任意两点的线段必定包涵Ω,则称Ω为平面上的凸集,给出平面上4个点集的图形如下(阴影区域及其边界): 其中为凸集的是 (写出所有凸集相应图形的序号).
[答案]②③
[解析]根据题意,在①④中任取两点,连接起来,如下图,不符合题意。


2.(湖南卷理15)若数列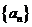 满足:对任意的
满足:对任意的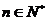 ,只有有限个正整数
,只有有限个正整数 使得
使得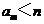 成立,记这样的
成立,记这样的 的个数为
的个数为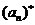 ,则得到一个新数列
,则得到一个新数列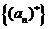 .例如,若数列
.例如,若数列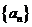 是
是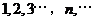 ,则数列
,则数列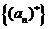 是
是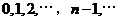 .已知对任意的
.已知对任意的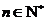 ,
,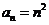 ,则
,则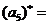 ,
,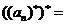 .
.
[答案]2,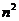
[解析]因为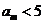 ,而
,而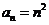 ,所以m=1,2,所以
,所以m=1,2,所以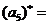 2.
2.
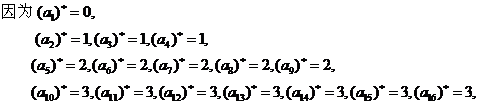
所以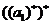 =1,
=1, 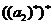 =4,
=4,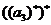 =9,
=9,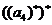 =16,
=16,
猜想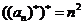
[命题意图]本题以数列为背景,通过新定义考察学生的自学能力、创新能力、探究能力,属难题。
3.(湖南卷文15)若规定E= 的子集
的子集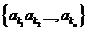 为E的第k个子集,其中k=
为E的第k个子集,其中k=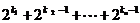 ,则(1)
,则(1) 是E的第____个子集;(2)E的第211个子集是_______
是E的第____个子集;(2)E的第211个子集是_______
[答案](1) 是E的第___5_个子集;
是E的第___5_个子集;
(2)E的第211个子集是___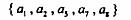 ____
____
4.(四川卷理16)设S为复数集C的非空子集.若对任意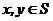 ,都有
,都有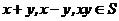 ,则称S为封闭集。下列命题:
,则称S为封闭集。下列命题:
①集合S={a+bi| 为整数,
为整数,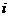 为虚数单位}为封闭集;
为虚数单位}为封闭集;
②若S为封闭集,则一定有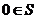 ;
;
③封闭集一定是无限集;
④若S为封闭集,则满足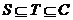 的任意集合
的任意集合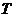 也是封闭集.
也是封闭集.
其中真命题是 (写出所有真命题的序号)
解析:直接验证可知①正确.
当S为封闭集时,因为x-y∈S,取x=y,得0∈S,②正确
对于集合S={0},显然满足素有条件,但S是有限集,③错误
取S={0},T={0,1},满足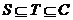 ,但由于0-1=-1ÏT,故T不是封闭集,④错误
,但由于0-1=-1ÏT,故T不是封闭集,④错误
答案:①②
5.(四川卷文16)设S为复数集C的非空子集.若对任意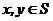 ,都有
,都有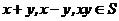 ,则称S为封闭集。下列命题:
,则称S为封闭集。下列命题:

 w_w w. k#s5_
w_w w. k#s5_
①集合S={a+b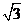 |
| 为整数}为封闭集;
为整数}为封闭集;
②若S为封闭集,则一定有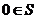 ;
;
③封闭集一定是无限集;
④若S为封闭集,则满足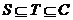 的任意集合
的任意集合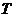 也是封闭集.
也是封闭集.
其中真命题是 (写出所有真命题的序号)
解析:直接验证可知①正确.
当S为封闭集时,因为x-y∈S,取x=y,得0∈S,②正确
对于集合S={0},显然满足素有条件,但S是有限集,③错误
取S={0},T={0,1},满足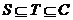 ,但由于0-1=-1ÏT,故T不是封闭集,④错误
,但由于0-1=-1ÏT,故T不是封闭集,④错误
答案:①②

 w_w w. k#s5_
w_w w. k#s5_
[考题分类]
(二)填空题(共8题)
1. (福建卷理12)若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积等于
。
(福建卷理12)若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积等于
。
[答案]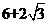
[解析]由正视图知:三棱柱是以底面边长为2,高为1的正三棱柱,所以底面积为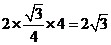 ,侧面积为
,侧面积为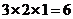 ,所以其表面积为
,所以其表面积为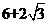 。
。
 [命题意图]本题考查立体几何中的三视图,考查同学们识图的
[命题意图]本题考查立体几何中的三视图,考查同学们识图的
能力、空间想象能力等基本能力。
2.(湖南卷理13文13)图3中的三个直角三角形是一个体积为
20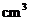 的几何体的三视图,则
的几何体的三视图,则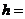
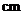 .
.
3. (辽宁卷理15文16)如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.
(辽宁卷理15文16)如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.
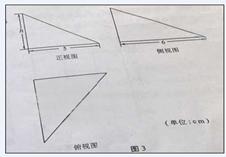
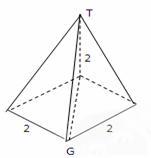

4.(全国Ⅰ新卷理14)正视图为一个三角形的几何体可以是______(写出三种)
[解析]三棱锥、三棱柱、圆锥等.
5.(全国Ⅰ新卷文15)一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的_______(填入所有可能的几何体前的编号)
①三棱锥 ②四棱锥 ③三棱柱 ④四棱柱 ⑤圆锥 ⑥圆柱
[答案]①②③⑤.
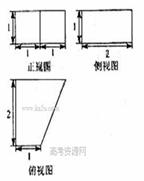
6.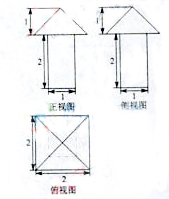 (天津卷理12)一个几何体的三视图如图所示,则这个几何体的体积为
(天津卷理12)一个几何体的三视图如图所示,则这个几何体的体积为
[答案]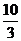
[解析]由三视图知:该几何体是一个底面边长为1、高为2的正四棱柱与一个底面边长为2、高为1的正四棱锥组成的组合体.因为正四棱柱的体积为2, 正四棱锥的体积为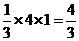 ,故该几何体的体积为
,故该几何体的体积为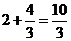 .
.
 [命题意图]本题考查立体几何中的三视图以及棱柱与棱锥体积的求解,考查空间想象能力、识图能力。
[命题意图]本题考查立体几何中的三视图以及棱柱与棱锥体积的求解,考查空间想象能力、识图能力。
7.(天津卷文12)一个几何体的三视图如图所示,则这个几何体的体积为 。
[答案]3
[解析]由三视图知,该几何体是一个底面为直角梯形的直棱柱,棱柱的高为1,梯形的上下底面边长分别为1、2,梯形的高为2,所以这个几何体的体积为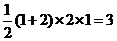 。
。
[命题意图]本题考查本题考查立体几何中的三视图以及棱柱体积的求解,考查空间想象能力与识图能力。
8.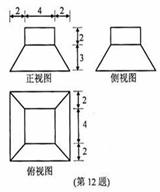 (浙江卷理12)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是___________
(浙江卷理12)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是___________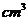 .
.
解析:图为一四棱台和长方体的组合体的三视图,由卷中所给公式计算得体积为144,本题主要考察了对三视图所表达示的空间几何体的识别以及几何体体积的计算,属容易题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com