
题目列表(包括答案和解析)
6.(辽宁卷理12)有四根长都为2的直铁条,若再选两根长都为a的直铁条,使这六根铁条端点处相连能够焊接成一个三棱锥形的铁架,则a的取值范围是
(A)(0,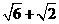 ) (B)(1,
) (B)(1,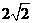 ) (C) (
) (C) (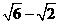 ,
,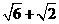 ) (D) (0,
) (D) (0,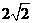 )
)
5.(江西卷文11)如图,M是正方体 的棱
的棱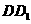 的中点,给出下列命题
的中点,给出下列命题
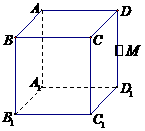 ①过M点有且只有一条直线与直线
①过M点有且只有一条直线与直线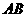 、
、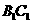 都相交;
都相交;
②过M点有且只有一条直线与直线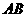 、
、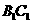 都垂直;
都垂直;
③过M点有且只有一个平面与直线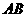 、
、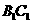 都相交;
都相交;
④过M点有且只有一个平面与直线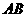 、
、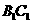 都平行.
都平行.
其中真命题是:
A.②③④ B.①③④ C.①②④ D.①②③
[答案]C
[解析]考查立体几何图形中相交平行垂直性质
4.(江西卷理10)过正方体 的顶点A作直线L,使L与棱
的顶点A作直线L,使L与棱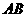 ,
, ,
, 所成的角都相等,这样的直线L可以作
所成的角都相等,这样的直线L可以作
A.1条 B.2条 C.3条 D.4条
[答案]D
[解析]考查空间感和线线夹角的计算和判断,重点考查学生分类、划归转化的能力。第一类:通过点A位于三条棱之间的直线有一条体对角线AC1,第二类:在图形外部和每条棱的外角和另2条棱夹角相等,有3条,合计4条。
3.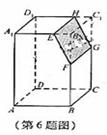 (福建卷理6)如图,若
(福建卷理6)如图,若 是长方体
是长方体 被平面
被平面 截去几何体
截去几何体 后得到的几何体,其中E为线段
后得到的几何体,其中E为线段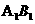 上异于
上异于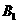 的点,F为线段
的点,F为线段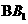 上异于
上异于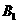 的点,且
的点,且 ∥
∥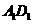 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A.  ∥
∥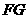 B.四边形
B.四边形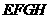 是矩形 C.
是矩形 C.  是棱柱 D.
是棱柱 D.  是棱台
是棱台
[答案]D
[解析]因为 ∥
∥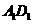 ,
,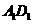 ∥
∥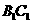 ,所以
,所以 ∥
∥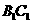 ,又
,又
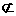 平面
平面 ,
,
所以 ∥平面
∥平面 ,又
,又
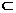 平面
平面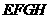 ,平面
,平面 平面
平面 =
=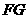 ,
,
所以 ∥
∥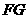 ,故
,故 ∥
∥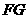 ∥
∥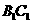 ,所以选项A、C正确;因为
,所以选项A、C正确;因为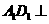 平面
平面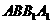 ,
,
 ∥
∥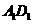 ,所以
,所以
 平面
平面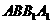 ,又
,又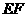
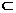 平面
平面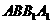 ,
故
,
故
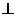
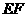 ,所以选项B也正确,故选D。
,所以选项B也正确,故选D。
[命题意图]本题考查空间中直线与平面平行、垂直的判定与性质,考查同学们的空间想象能力和逻辑推理能力。
2.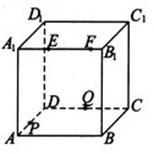 (北京卷文8)如图,正方体
(北京卷文8)如图,正方体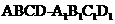 的棱长为2,动点E、F在棱
的棱长为2,动点E、F在棱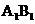 上。点Q是CD的中点,动点P在棱AD上,若EF=1,DP=x,
上。点Q是CD的中点,动点P在棱AD上,若EF=1,DP=x, E=y(x,y大于零),则三棱锥P-EFQ的体积:
E=y(x,y大于零),则三棱锥P-EFQ的体积:
(A)与x,y都有关; (B)与x,y都无关;
(C)与x有关,与y无关; (D)与y有关,与x无关;

1.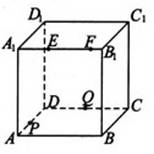 (北京卷理8)如图,正方体ABCD-
(北京卷理8)如图,正方体ABCD-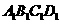 的棱长为2,动点E、F在棱
的棱长为2,动点E、F在棱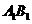 上,动点P,Q分别在棱AD,CD上,若EF=1,
上,动点P,Q分别在棱AD,CD上,若EF=1, E=x,DQ=y,DP=z(x,y,z大于零),则四面体PEFQ的体积
E=x,DQ=y,DP=z(x,y,z大于零),则四面体PEFQ的体积
(A)与x,y,z都有关 (B)与x有关,与y,z无关
(C)与y有关,与x,z无关 (D)与z有关,与x,y无关
[答案]D.
解析:这道题目延续了北京高考近年8,14,20的风格,即在变化中寻找不变,从图中可以分析出,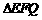 的面积永远不变,为面
的面积永远不变,为面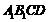 面积的
面积的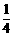 ,而当
,而当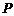 点变化时,它到面
点变化时,它到面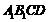 的距离是变化的,因此会导致四面体体积的变化。
的距离是变化的,因此会导致四面体体积的变化。
4.(上海春卷15)若空间三条直线a、b、c满足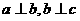 ,则直线a与c ( )
,则直线a与c ( )
(A)一定平行; (B)一定相交;
(C)一定是异面直线; (D)平行、相交、是异面直线都有可能
答案:D
解析:由直线的位置关系可知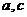 可能平行,可以相交,也可以异面,故选D。
可能平行,可以相交,也可以异面,故选D。
3.(浙江卷理6)设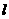 ,
, 是两条不同的直线,
是两条不同的直线,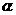 是一个平面,则下列命题正确的是
是一个平面,则下列命题正确的是
(A)若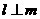 ,
,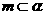 ,则
,则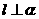 (B)若
(B)若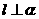 ,
,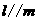 ,则
,则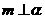
(C)若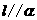 ,
,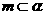 ,则
,则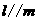 (D)若
(D)若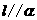 ,
,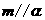 ,则
,则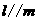
解析:选B,可对选项进行逐个检查。本题主要考察了立体几何中线面之间的位置关系及其中的公理和判定定理,也蕴含了对定理公理综合运用能力的考察,属中档题
2.(山东卷理3文4)在空间,下列命题正确的是
(A)平行直线的平行投影重合
(B)平行于同一直线的两个平面平行
(C)垂直于同一平面的两个平面平行
(D)垂直于同一平面的两条直线平行
[解析]由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可以很容易得出答案D。
[命题意图]本题考查空间直线与平面的位置关系及线面垂直与平行的判定与性质,基础题。
1.(湖北卷文4)用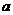 、
、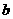 、
、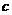 表示三条不同的直线,
表示三条不同的直线,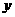 表示平面,给出下列命题:
表示平面,给出下列命题:
①若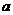 ∥
∥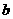 ,
,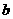 ∥
∥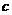 ,则
,则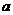 ∥
∥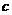 ;②若
;②若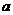 ⊥
⊥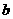 ,
,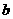 ⊥
⊥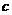 ,则
,则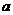 ⊥
⊥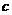 ;
;
③若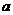 ∥
∥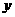 ,
,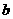 ∥
∥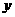 ,则
,则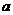 ∥
∥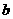 ;④若
;④若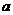 ⊥
⊥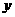 ,
,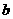 ⊥
⊥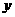 ,则
,则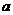 ∥
∥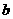 .
.
A. ①② B. ②③ C. ①④ D.③④

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com