
题目列表(包括答案和解析)
8.(重庆卷文8)若直线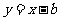 与曲线
与曲线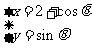 ,(
,(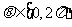 )有两个不同的公共点,则实数
)有两个不同的公共点,则实数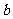 的取值范围为
的取值范围为
(A)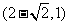 (B)
(B)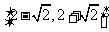
(C)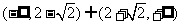 (D)
(D)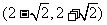
 [答案]D
[答案]D
[解析]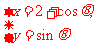 化为普通方程
化为普通方程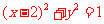 ,表示圆,
,表示圆,
因为直线与圆有两个不同的交点,所以 解得
解得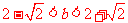
法2:利用数形结合进行分析得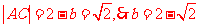
同理分析,可知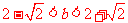
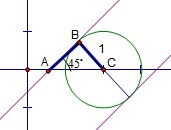
7.(重庆卷理8)直线y=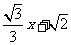 与圆心为D的圆
与圆心为D的圆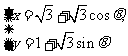
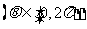 交与A、B两点,则直线AD与BD的倾斜角之和为
交与A、B两点,则直线AD与BD的倾斜角之和为
A. 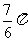 B.
B. 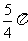 C.
C. 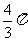 D.
D.

[答案]C
解析:数形结合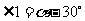
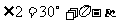
由圆的性质可知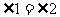
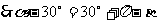
故
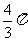
6.(全国Ⅰ卷理11文11)已知圆O的半径为1,PA、PB为该圆的两条切线,A、B为俩切点,那么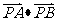 的最小值为
的最小值为
(A)  (B)
(B) (C)
(C)  (D)
(D)
 [答案]D[命题意图]本小题主要考查向量的数量积运算与圆的切线长定理,着重考查最值的求法--判别式法,同时也考查了考生综合运用数学知识解题的能力及运算能力.
[答案]D[命题意图]本小题主要考查向量的数量积运算与圆的切线长定理,着重考查最值的求法--判别式法,同时也考查了考生综合运用数学知识解题的能力及运算能力.
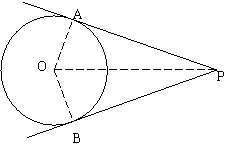
[解析]如图所示:设PA=PB=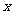
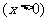 ,∠APO=
,∠APO=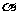 ,则∠APB=
,则∠APB= ,PO=
,PO=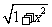 ,
,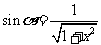 ,
,
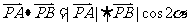 =
=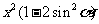 =
=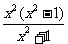 =
=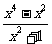 ,令
,令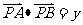 ,则
,则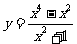 ,即
,即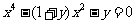 ,由
,由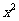 是实数,所以
是实数,所以
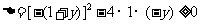 ,
,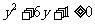 ,解得
,解得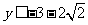 或
或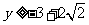 .故
.故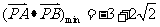 .此时
.此时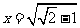 .
.
5. (江西卷文10)直线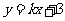 与圆
与圆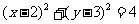 相交于M、N两点,若|MN|≥
相交于M、N两点,若|MN|≥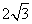 ,则
,则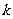 的取值范围是
的取值范围是
A.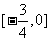 B.
B.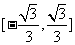 C.
C.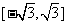 D.
D.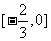
[答案]B
[解析]考查相交弦问题。法一、可联立方程组利用弦长公式求|MN|再结合|MN|≥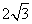 可得答案
可得答案
法二、利用圆的性质知:圆心到直线的距离的平方加上弦长的一半的平方等于半径的平方求出|MN|再结合|MN|≥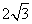 可得答案
可得答案
4. (江西卷理8)直线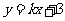 与圆
与圆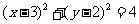 相交于M,N两点,若|MN|≥
相交于M,N两点,若|MN|≥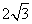 ,则
,则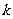 的取值范围是
的取值范围是
A.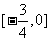 B.
B.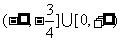 C.
C.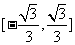 D.
D.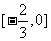
[答案]A
[解析]考查直线与圆的位置关系、点到直线距离公式,重点考察数形结合的运用.
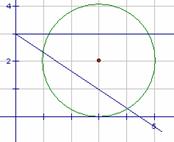 解法1:圆心的坐标为(3.,2),且圆与y轴相切.当
解法1:圆心的坐标为(3.,2),且圆与y轴相切.当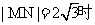 ,由点到直线距离公式,解得
,由点到直线距离公式,解得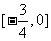 ;
;
解法2:数形结合,如图由垂径定理得夹在两直线之间即可, 不取 ,排除B,考虑区间不对称,排除C,利用斜率估值,选A
,排除B,考虑区间不对称,排除C,利用斜率估值,选A
3.(湖北卷理9文9)若直线y=x+b与曲线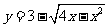 有公共点,则b的取值范围是
有公共点,则b的取值范围是
A. 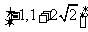 B.
B. 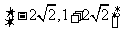 C.
C. 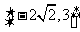 D.
D. 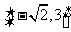
[答案]C
[解析]曲线方程可化简为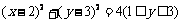 ,即表示圆心为(2,3)半径为2的半圆,依据数形结合,当直线
,即表示圆心为(2,3)半径为2的半圆,依据数形结合,当直线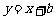 与此半圆相切时须满足圆心(2,3)到直线y=x+b距离等于2,解得
与此半圆相切时须满足圆心(2,3)到直线y=x+b距离等于2,解得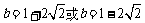 ,因为是下半圆故可得
,因为是下半圆故可得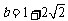 (舍),当直线过(0,3)时,解得b=3,故
(舍),当直线过(0,3)时,解得b=3,故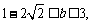 所以C正确.
所以C正确.
2.(广东卷文6)若圆心在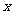 轴上、半径为
轴上、半径为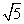 的圆
的圆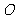 位于
位于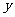 轴左侧,且与直线
轴左侧,且与直线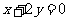 相切,则圆
相切,则圆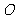 的方程是
的方程是
A.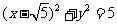 B.
B.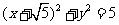
C.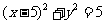 D.
D.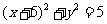
[解析]由题意知,圆心在y轴左侧,排除A、C
在 ,
,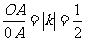 ,故
,故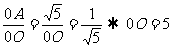 ,选D.
,选D.
1.(安徽卷理7)设曲线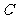 的参数方程为
的参数方程为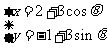 (
(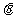 为参数),直线
为参数),直线 的方程为
的方程为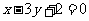 ,则曲线
,则曲线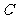 上到直线
上到直线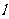 距离为
距离为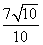 的点的个数为
的点的个数为
A、1 B、2 C、3 D、4
[答案]B
[解析]化曲线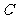 的参数方程为普通方程:
的参数方程为普通方程: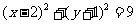 ,圆心
,圆心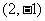 到直线
到直线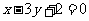 的距离
的距离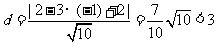 ,直线和圆相交,过圆心和
,直线和圆相交,过圆心和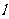 平行的直线和圆的2个交点符合要求,又
平行的直线和圆的2个交点符合要求,又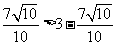 ,在直线
,在直线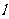 的另外一侧没有圆上的点符合要求,所以选B.
的另外一侧没有圆上的点符合要求,所以选B.
[方法总结]解决这类问题首先把曲线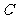 的参数方程为普通方程,然后利用圆心到直线的距离判断直线与圆的位置关系,这就是曲线
的参数方程为普通方程,然后利用圆心到直线的距离判断直线与圆的位置关系,这就是曲线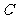 上到直线
上到直线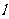 距离为
距离为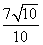 ,然后再判断知
,然后再判断知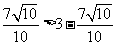 ,进而得出结论.
,进而得出结论.
2.(上海卷理16)直线l的参数方程是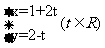 ,则l的方向向量是
,则l的方向向量是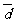 可以是( )
可以是( )
(A)(1,2) (B)(2,1) (C)(-2,1) (D)(1,-2)
[答案](C)
[解析]直线l的一般方程是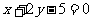 ,
,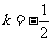 ,所以C正确
,所以C正确
1.(安徽卷文4)过点(1,0)且与直线x-2y-2=0平行的直线方程是
(A)x-2y-1=0 (B)x-2y+1=0
(C)2x+y-2=0 (D)x+2y-1=0
[答案]A
[解析]设直线方程为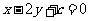 ,又经过
,又经过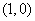 ,故
,故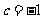 ,所求方程为
,所求方程为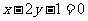 .
.
[方法技巧]因为所求直线与与直线x-2y-2=0平行,所以设平行直线系方程为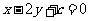 ,代入此直线所过的点的坐标,得参数值,进而得直线方程.也可以用验证法,判断四个选项中方程哪一个过点(1,0)且与直线x-2y-2=0平行.
,代入此直线所过的点的坐标,得参数值,进而得直线方程.也可以用验证法,判断四个选项中方程哪一个过点(1,0)且与直线x-2y-2=0平行.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com