
题目列表(包括答案和解析)
3. (湖南卷理19)为了考察冰川的融化状况,一支科考队在某冰川上相距8km的A,B两点各建一个考察基地.视冰川面为平面形,以过A,B两点的直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系(图6).在直线
(湖南卷理19)为了考察冰川的融化状况,一支科考队在某冰川上相距8km的A,B两点各建一个考察基地.视冰川面为平面形,以过A,B两点的直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系(图6).在直线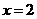 的右侧,考察范围为到点B的距离不超过
的右侧,考察范围为到点B的距离不超过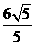 km的区域;在直线
km的区域;在直线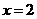 的左侧,考察范围为到A,B两点的距离之和不超过
的左侧,考察范围为到A,B两点的距离之和不超过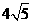 km的区域.
km的区域.
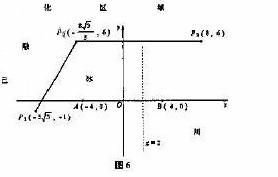 (Ⅰ)求考察区域边界曲线的方程;
(Ⅰ)求考察区域边界曲线的方程;
(Ⅱ)如图6所示,设线段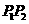 ,
,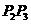 是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍,求冰川边界线移动到考察区域所需的最短时间.
是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍,求冰川边界线移动到考察区域所需的最短时间.
[解析](Ⅰ)设边界曲线上点P的坐标为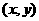 .当
.当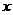 ≥2时,由题意知
≥2时,由题意知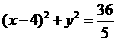
当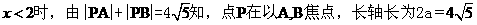
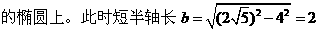 ,因而其方程为
,因而其方程为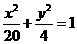
故考察区域边界曲线(如图)的方程为

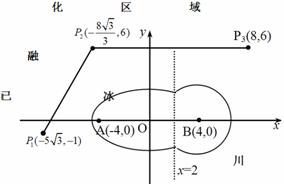
(Ⅱ)设过点P1,P2的直线为l1,点P2,P3的直线为l2,则直线l1,l2的方程分别为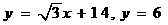 ,
,


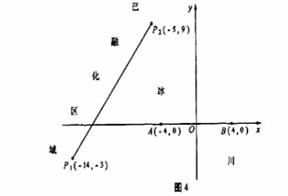 [命题意图]本题以应用题为背景,考查考察考生数学建模能力,考查圆的方程、椭圆的定义与方程、直线与圆锥曲线的位置关系、等比数列求和。本题属难题。
[命题意图]本题以应用题为背景,考查考察考生数学建模能力,考查圆的方程、椭圆的定义与方程、直线与圆锥曲线的位置关系、等比数列求和。本题属难题。
2.(湖北卷理19文20)已知一条曲线C在y轴右边,C上没一点到点F(1,0)的距离减去它到y轴距离的差是1.
(Ⅰ)求曲线C的方程;
(Ⅱ)是否存在正数m,对于过点M(m,0)且与曲线C有连个交点A,B的任一直线,都有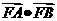 ﹤0 ? 若存在,求出m的取值范围;若不存在,请说明理由.
﹤0 ? 若存在,求出m的取值范围;若不存在,请说明理由.
1.(北京卷理19)在平面直角坐标系xOy中,点B与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于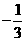 .
.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由。
解:(1)因点B与(-1,1)关于原点对称,得B点坐标为(1,-1)。
设P点坐标为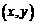 ,则
,则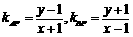 ,由题意得
,由题意得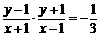 ,
,
化简得: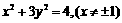 。
。
即P点轨迹为: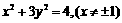
(2)因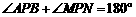 ,可得
,可得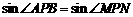 ,
,
又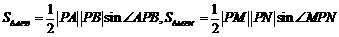 ,
,
若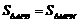 ,则有
,则有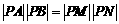 , 即
, 即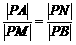
设P点坐标为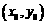 ,则有:
,则有: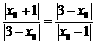
解得: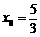 ,又因
,又因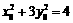 ,解得
,解得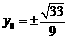 。
。
故存在点P使得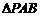 与
与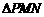 的面积相等,此时P点坐标为
的面积相等,此时P点坐标为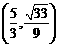 或
或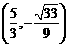
1.(上海卷理3文8)动点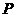 到点
到点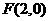 的距离与它到直线
的距离与它到直线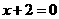 的距离相等,则
的距离相等,则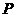 的轨迹方程为
。
的轨迹方程为
。
答案:y2=8x 。
命题立意:考查抛物线定义及标准方程
解析:定义知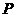 的轨迹是以
的轨迹是以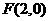 为焦点的抛物线,p=2所以其方程为y2=8x
为焦点的抛物线,p=2所以其方程为y2=8x
3.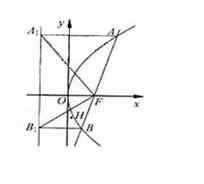 (浙江卷文22)已知m是非零实数,抛物线
(浙江卷文22)已知m是非零实数,抛物线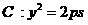 (p>0)的焦点F在直线
(p>0)的焦点F在直线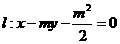 上。
上。
(I)若m=2,求抛物线C的方程
(II)设直线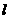 与抛物线C交于A、B,△A
与抛物线C交于A、B,△A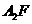 ,△
,△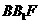 的重
的重
心分别为G,H,求证:对任意非零实数m,抛物线C的准线与x轴
的焦点在以线段GH为直径的圆外
解析:本题主要考查抛物线几何性质,直线与抛物线、点与圆的位置关系等基础知识,同时考查解析几何的基本思想方法和运算求解能力。
(Ⅰ)解:因为焦点F(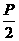 ,0)在直线l上,得
,0)在直线l上,得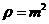
又m=2,故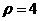 所以抛物线C的方程为
所以抛物线C的方程为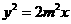
设A(x1,y1) , B(x2,y2)
由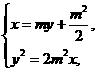 消去x得y2-2m3y-m4=0,
消去x得y2-2m3y-m4=0,
由于m≠0,故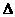 =4m6+4m4>0,
=4m6+4m4>0,
且有y1+y2=2m3,y1y2=-m4,
设M1,M2分别为线段AA1,BB1的中点,
由于2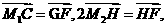
可知G(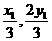 ),H(
),H(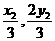 ),
),
所以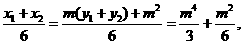
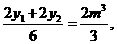
所以GH的中点M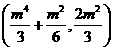 .
.
设R是以线段GH为直径的圆的半径,
则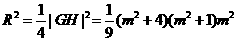
设抛物线的标准线与x轴交点N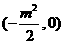 ,
,
则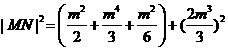
=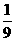 m4(m4+8
m2+4)
m4(m4+8
m2+4)
=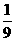 m4[(m2+1)(
m2+4)+3m2]
m4[(m2+1)(
m2+4)+3m2]
>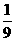 m2
(m2+1)( m2+4)=R2.
m2
(m2+1)( m2+4)=R2.
故N在以线段GH为直径的圆外.
2. (全国Ⅰ卷理21文22)已知抛物线
(全国Ⅰ卷理21文22)已知抛物线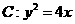 的焦点为F,过点
的焦点为F,过点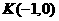 的直线
的直线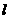 与
与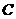 相交于
相交于 、
、 两点,点A关于
两点,点A关于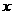 轴的对称点为D .
轴的对称点为D .
(Ⅰ)证明:点F在直线BD上;
(Ⅱ)设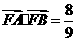 ,求
,求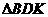 的内切圆M的方程 .
的内切圆M的方程 .
[命题意图]本小题为解析几何与平面向量综合的问题,主要考查抛物线的性质、直线与圆的位置关系,直线与抛物线的位置关系、圆的几何性质与圆的方程的求解、平面向量的数量积等知识,考查考生综合运用数学知识进行推理论证的能力、运算能力和解决问题的能力,同时考查了数形结合思想、设而不求思想.
[解析]设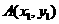 ,
,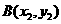 ,
,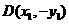 ,
,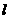 的方程为
的方程为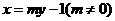 .
.

(Ⅱ)由①知,
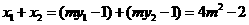
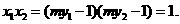
因为 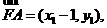
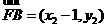 ,
,

故
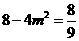 ,解得
,解得
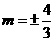
所以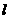 的方程为
的方程为
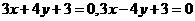
又由①知 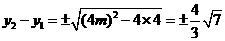
故直线BD的斜率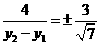 ,
,
因而直线BD的方程为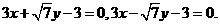
因为KF为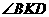 的平分线,故可设圆心
的平分线,故可设圆心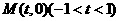 ,
,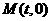 到
到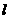 及BD的距离分别为
及BD的距离分别为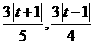 .
.
由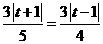 得
得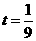 ,或
,或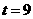 (舍去),
(舍去),
故 圆M的半径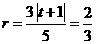 .所以圆M的方程为
.所以圆M的方程为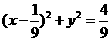 .
.
1.(福建卷文19)已知抛物线C的方程C:y 2 =2 p x(p>0)过点A(1,-2).
(I)求抛物线C的方程,并求其准线方程;
(II)是否存在平行于OA(O为坐标原点)的直线l,使得直线l与抛物线C有公共点,且直线OA与l 的距离等于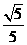 ?若存在,求出直线l的方程;若不存在,说明理由。
?若存在,求出直线l的方程;若不存在,说明理由。
6.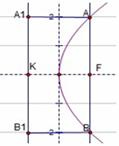 (重庆卷文13)已知过抛物线y2=4x的焦点F的直线交该抛物线于A、B两点,|AF|=2,则|BF|=
。
(重庆卷文13)已知过抛物线y2=4x的焦点F的直线交该抛物线于A、B两点,|AF|=2,则|BF|=
。
[答案]2
[解析]由抛物线的定义可知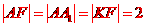
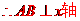 故
故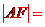
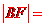 2
2
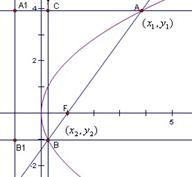
5.(重庆卷理14)已知以F为焦点的抛物线 上的两点A、B满足
上的两点A、B满足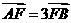 ,则弦AB的中点到准线的距离为___________.
,则弦AB的中点到准线的距离为___________.
 [答案]
[答案]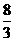
解析:设BF=m,由抛物线的定义知
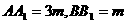
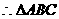 中,AC=2m,AB=4m,
中,AC=2m,AB=4m,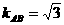
直线AB方程为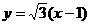
与抛物线方程联立消y得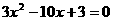
所以AB中点到准线距离为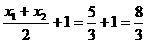
4.(浙江卷理13)设抛物线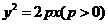 的焦点为
的焦点为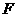 ,点
,点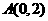 .若线段
.若线段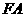 的中点
的中点 在抛物线上,则
在抛物线上,则 到该抛物线准线的距离为_____________。
到该抛物线准线的距离为_____________。
解析:利用抛物线的定义结合题设条件可得出p的值为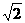 ,B点坐标为(
,B点坐标为(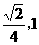 )所以点B到抛物线准线的距离为
)所以点B到抛物线准线的距离为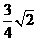 ,本题主要考察抛物线的定义及几何性质,属容易题
,本题主要考察抛物线的定义及几何性质,属容易题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com