
题目列表(包括答案和解析)
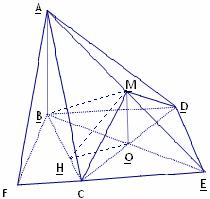
15. (江西卷文20)如图,
(江西卷文20)如图,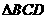 与
与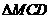 都是边长为2的正三角形,平面
都是边长为2的正三角形,平面 平面
平面 ,
,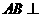 平面
平面 ,
,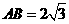 .
.
(1)求直线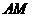 与平面
与平面 所成的角的大小;
所成的角的大小;
(2)求平面 与平面
与平面 所成的二面角的正弦值.
所成的二面角的正弦值.
 [解析]本题主要考查了考查立体图形的空间感、线面角、二面角、空间向量、二面角平面角的判断有关知识,同时也考查了空间想象能力和推理能力
[解析]本题主要考查了考查立体图形的空间感、线面角、二面角、空间向量、二面角平面角的判断有关知识,同时也考查了空间想象能力和推理能力
解法一:(1)取CD中点O,连OB,OM,则OB⊥CD,OM⊥CD.
又平面 平面
平面 ,则MO⊥平面
,则MO⊥平面 ,所以MO∥AB,A、B、O、M共面.延长AM、BO相交于E,则∠AEB就是AM与平面BCD所成的角.
,所以MO∥AB,A、B、O、M共面.延长AM、BO相交于E,则∠AEB就是AM与平面BCD所成的角.
OB=MO=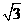 ,MO∥AB,则
,MO∥AB,则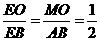 ,
,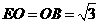 ,所以
,所以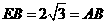 ,故
,故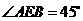 .
.
 (2)CE是平面
(2)CE是平面 与平面
与平面 的交线.
的交线.
由(1)知,O是BE的中点,则BCED是菱形.
作BF⊥EC于F,连AF,则AF⊥EC,∠AFB就是二面角A-EC-B的平面角,设为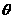 .
.
因为∠BCE=120°,所以∠BCF=60°.
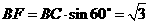 ,
,
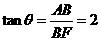 ,
,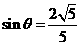
所以,所求二面角的正弦值是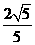 .
.
解法二:取CD中点O,连OB,OM,则OB⊥CD,OM⊥CD,又平面 平面
平面 ,则MO⊥平面
,则MO⊥平面 .
.
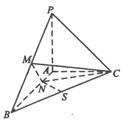
 以O为原点,直线OC、BO、OM为x轴,y轴,z轴,建立空间直角坐标系如图.
以O为原点,直线OC、BO、OM为x轴,y轴,z轴,建立空间直角坐标系如图.
OB=OM=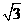 ,则各点坐标分别为O(0,0,0),C(1,0,0),M(0,0,
,则各点坐标分别为O(0,0,0),C(1,0,0),M(0,0,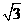 ),B(0,-
),B(0,-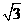 ,0),A(0,-
,0),A(0,-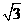 ,2
,2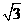 ),
),
(1)设直线AM与平面BCD所成的角为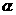 .
.
因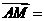 (0,
(0,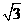 ,
,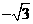 ),平面
),平面 的法向量为
的法向量为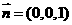 .则有
.则有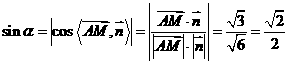 ,所以
,所以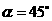 .
.
(2)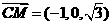 ,
,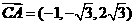 .
.
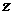 设平面ACM的法向量为
设平面ACM的法向量为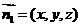 ,
,
由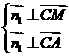 得
得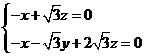 .解得
.解得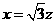 ,
,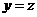 ,取
,取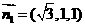 .
.
又平面BCD的法向量为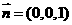 ,则
,则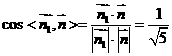
 设所求二面角为
设所求二面角为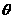 ,则
,则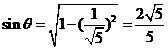 .
.
14.(江西卷理20)如图,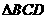 与
与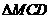 都是边长为2的正三角形,平面
都是边长为2的正三角形,平面 平面
平面 ,
,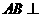 平面
平面 ,
,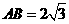 .
.
(1)求点 到平面
到平面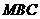 的距离;
的距离;
(2)求平面 与平面
与平面 所成二面角的正弦值.
所成二面角的正弦值.
[解析]本题以图形拼折为载体主要考查了考查立体图形的空间感、点到直线的距离、二面角、空间向量、二面角平面角的判断有关知识,同时也考查了空间想象能力和推理能力
解法一:(1)取CD中点O,连OB,OM,则OB⊥CD,OM⊥CD.又平面 平面
平面 ,则MO⊥平面
,则MO⊥平面 ,所以MO∥AB,A、B、O、M共面.延长AM、BO相交于E,则∠AEB就是AM与平面BCD所成的角.OB=MO=
,所以MO∥AB,A、B、O、M共面.延长AM、BO相交于E,则∠AEB就是AM与平面BCD所成的角.OB=MO=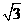 ,MO∥AB,MO//面ABC,M、O到平面ABC的距离相等,作OH
,MO∥AB,MO//面ABC,M、O到平面ABC的距离相等,作OH BC于H,连MH,则MH
BC于H,连MH,则MH BC,求得:
BC,求得:
 OH=OCsin600=
OH=OCsin600=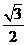 ,MH=
,MH=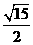 ,利用体积相等得:
,利用体积相等得: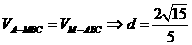 。
。
(2)CE是平面 与平面
与平面 的交线.
的交线.
由(1)知,O是BE的中点,则BCED是菱形.
作BF⊥EC于F,连AF,则AF⊥EC,∠AFB就是二面角A-EC-B的平面角,设为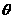 .
.
因为∠BCE=120°,所以∠BCF=60°.
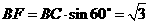 ,
,
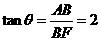 ,
,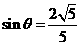
所以,所求二面角的正弦值是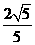 .
.
[点评]传统方法在处理时要注意到辅助线的处理,一般采用射影、垂线、平行线等特殊位置的元素解决
 解法二:取CD中点O,连OB,OM,则OB⊥CD,OM⊥CD,又平面
解法二:取CD中点O,连OB,OM,则OB⊥CD,OM⊥CD,又平面 平面
平面 ,则MO⊥平面
,则MO⊥平面 .
.
以O为原点,直线OC、BO、OM为x轴,y轴,z轴,建立空间直角坐标系如图.
OB=OM=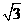 ,则各点坐标分别为O(0,0,0),C(1,0,0),M(0,0,
,则各点坐标分别为O(0,0,0),C(1,0,0),M(0,0,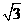 ),B(0,-
),B(0,-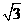 ,0),A(0,-
,0),A(0,-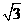 ,2
,2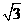 ),
),
(1)设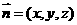 是平面MBC的法向量,则
是平面MBC的法向量,则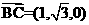 ,
,
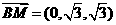 ,由
,由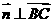 得
得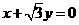 ;由
;由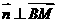 得
得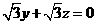 ;取
;取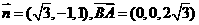 ,则距离
,则距离
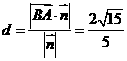
(2)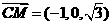 ,
,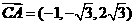 .
.

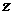 设平面ACM的法向量为
设平面ACM的法向量为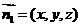 ,
,
由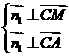 得
得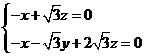 .解得
.解得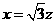 ,
,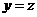 ,取
,取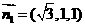 .
.
又平面BCD的法向量为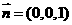 ,则
,则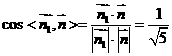
设所求二面角为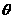 ,则
,则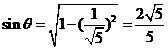 .
.
[点评]向量方法作为沟通代数和几何的工具在考察中越来越常见,此类方法的要点在于建立恰当的坐标系,便于计算,位置关系明确,以计算代替分析,起到简化的作用,但计算必须慎之又慎
13.
 (江苏卷16)如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900
(江苏卷16)如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900
求证:PC⊥BC
求点A到平面PBC的距离
[解析] 本小题主要考查直线与平面、平面与平面的位置关系,考查几何体的体积,考查空间想象能力、推理论证能力和运算能力。满分14分。
(1)证明:因为PD⊥平面ABCD,BC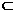 平面ABCD,所以PD⊥BC。
平面ABCD,所以PD⊥BC。
由∠BCD=900,得CD⊥BC,
又PD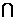 DC=D,PD、DC
DC=D,PD、DC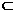 平面PCD,
平面PCD,
所以BC⊥平面PCD。
因为PC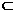 平面PCD,故PC⊥BC。
平面PCD,故PC⊥BC。
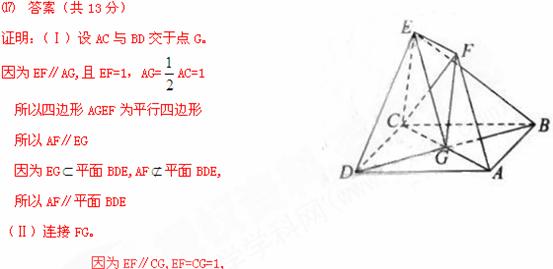
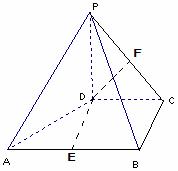 (2)(方法一)分别取AB、PC的中点E、F,连DE、DF,则:
(2)(方法一)分别取AB、PC的中点E、F,连DE、DF,则:
易证DE∥CB,DE∥平面PBC,点D、E到平面PBC的距离相等。
又点A到平面PBC的距离等于E到平面PBC的距离的2倍。
由(1)知:BC⊥平面PCD,所以平面PBC⊥平面PCD于PC,
因为PD=DC,PF=FC,所以DF⊥PC,所以DF⊥平面PBC于F。
易知DF=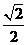 ,故点A到平面PBC的距离等于
,故点A到平面PBC的距离等于 。
。
(方法二)体积法:连结AC。设点A到平面PBC的距离为h。
因为AB∥DC,∠BCD=900,所以∠ABC=900。
从而AB=2,BC=1,得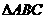 的面积
的面积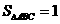 。
。
由PD⊥平面ABCD及PD=1,得三棱锥P-ABC的体积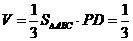 。
。
因为PD⊥平面ABCD,DC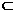 平面ABCD,所以PD⊥DC。
平面ABCD,所以PD⊥DC。
又PD=DC=1,所以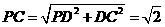 。
。
由PC⊥BC,BC=1,得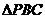 的面积
的面积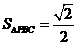 。
。
由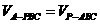 ,
,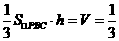 ,得
,得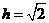 ,
,
 故点A到平面PBC的距离等于
故点A到平面PBC的距离等于 。
。
12.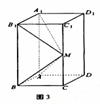 (湖南卷文18)如图所示,在长方体
(湖南卷文18)如图所示,在长方体 中,AB=AD=1,AA1=2,M是棱CC1的中点
中,AB=AD=1,AA1=2,M是棱CC1的中点
(Ⅰ)求异面直线A1M和C1D1所成的角的正切值;
(Ⅱ)证明:平面ABM⊥平面A1B1M1
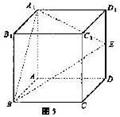
11.(湖南卷理18)如图5所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点。
(Ⅰ)求直线BE与平面ABB1A1所成的角的正弦值;
(Ⅱ)在棱C1D1上是否存在一点F,使B1F//平面A1BE?证明你的结论。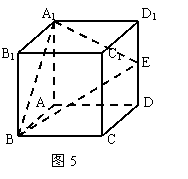
[解析]


所以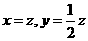 ,取
,取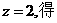 n
n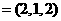 .
.
设F是棱C1D1上的点,则F(t,1,1)(0≤t≤1),又B1(1,0,1),所以
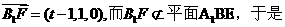
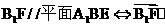 n
n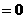
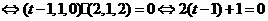
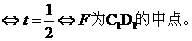 这说明在在棱C1D1上是否存在一点F(
这说明在在棱C1D1上是否存在一点F(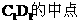 ),使B1F//平面A1BE
),使B1F//平面A1BE
解法2 如图(a)所示,取AA1的中点M,连结EM,BM,因为E是DD1的中点,四边形ADD1A1为正方形,所以EM//AD。
又在正方体ABCD-A1B1C1D1中。AD⊥平面ABB1A1,所以EM⊥ABB1A1,从而BM为直线BE在平面ABB1A1上的射影,∠EBM直线BE与平面ABB1A1所成的角.
设正方体的棱长为2,则EM=AD=2,BE=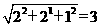 ,于是
,于是
在RT△BEM中,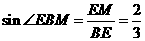

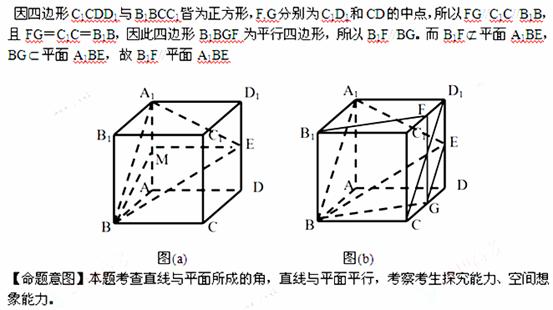
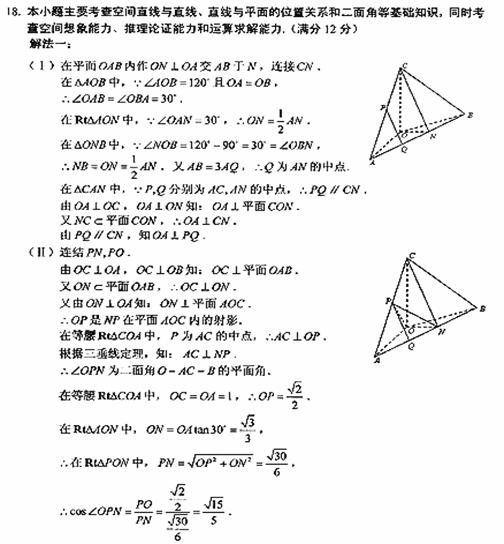
10.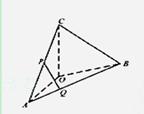 (湖北卷文18)如图,在四面体ABOC中,OC⊥OA。OC⊥OB,∠AOB=120°,且OA=OB=OC=1
(湖北卷文18)如图,在四面体ABOC中,OC⊥OA。OC⊥OB,∠AOB=120°,且OA=OB=OC=1
(Ⅰ)设P为AC的中点,Q在AB上且AB=3AQ,证明:PQ⊥OA;
(Ⅱ)求二面角O-AC-B的平面角的余弦值。
8. (广东卷文18)如图4,弧
(广东卷文18)如图4,弧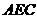 是半径为
是半径为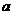 的半圆,
的半圆, 为直径,点
为直径,点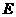 为弧AC的中点,点
为弧AC的中点,点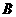 和点
和点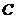 为线段
为线段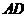 的三等分点,平面
的三等分点,平面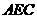 外一点
外一点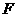 满足
满足
 平面
平面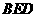 ,
,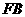 =
=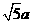 .
.
(1)证明: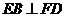 ;
;
(2)求点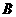 到平面
到平面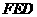 的距离.
的距离.
解析:(1)证明: 点E为弧AC的中点
点E为弧AC的中点

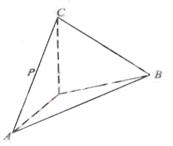
 9.(湖北卷理18)如图, 在四面体ABOC中,
9.(湖北卷理18)如图, 在四面体ABOC中, 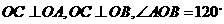 ,
且
,
且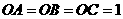
(Ⅰ)设为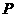 为
为 的中点,
证明: 在
的中点,
证明: 在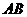 上存在一点
上存在一点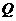 ,使
,使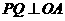 ,并计算
,并计算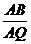 的值;
的值;
(Ⅱ)求二面角 的平面角的余弦值。
的平面角的余弦值。


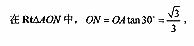

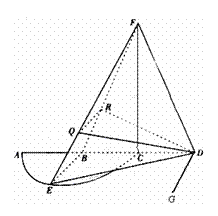
7. (广东卷理18)如图,弧AEC是半径为a的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点。平面AEC外一点F满足FB=FD=
(广东卷理18)如图,弧AEC是半径为a的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点。平面AEC外一点F满足FB=FD=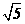 a,FE=
a,FE=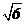 a
,
a
,
(1)证明:EB⊥FD;
(2)已知点Q,R分别为线段FE,FB上的点,使得FQ=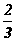 FE,FR=
FE,FR=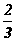 FB,求平面BED与平面RQD所成二面角的正弦值。
FB,求平面BED与平面RQD所成二面角的正弦值。

 (2)设平面
(2)设平面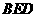 与平面RQD的交线为
与平面RQD的交线为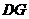 .
.
由BQ=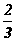 FE,FR=
FE,FR=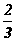 FB知,
FB知, 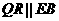 .
.
而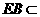 平面
平面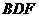 ,∴
,∴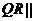 平面
平面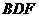 ,
,
而平面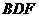
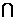 平面
平面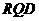 =
=
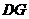 ,
,
∴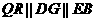 .
.
由(1)知,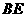
 平面
平面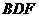 ,∴
,∴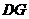
 平面
平面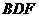 ,
,
而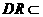 平面
平面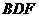 ,
,
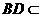 平面
平面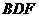 ,
,
∴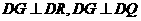 ,
,
∴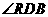 是平面
是平面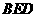 与平面
与平面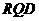 所成二面角的平面角.
所成二面角的平面角.
在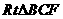 中,
中,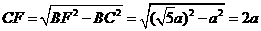 ,
,
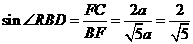 ,
,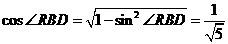 .
.
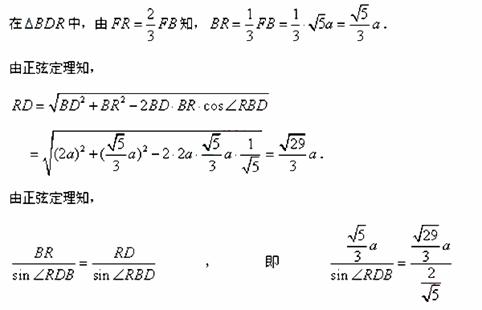
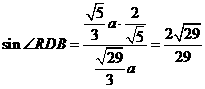 .
.
故平面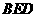 与平面
与平面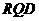 所成二面角的正弦值是
所成二面角的正弦值是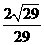 .
.
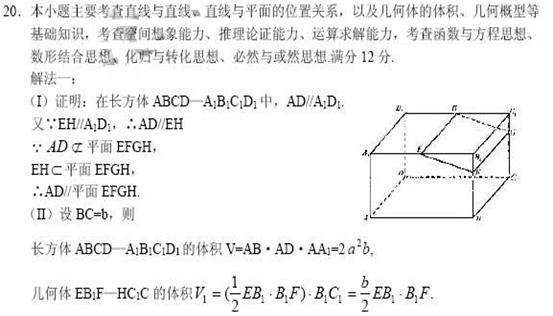
6. (福建卷文20)如图,在长方体ABCD-A1B1C1D1 中,E,H分别是棱A1B1,D1C1上的点(点E与B1 不重合),且EH∥A1 D1. 过EH的平面与棱BB1 ,CC1 相交,交点分别为F,G。
(福建卷文20)如图,在长方体ABCD-A1B1C1D1 中,E,H分别是棱A1B1,D1C1上的点(点E与B1 不重合),且EH∥A1 D1. 过EH的平面与棱BB1 ,CC1 相交,交点分别为F,G。
(I)证明:AD∥平面EFGH;
(II)设AB=2AA1 =2 a .在长方体ABCD-A1B1C1D1 内随机选取一点。记该点取自几何体A1ABFE-D1DCGH内的概率为p,当点E,F分别在棱A1B1上运动且满足EF=a时,求p的最小值.

5.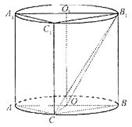
 (福建卷理18)如图,圆柱
(福建卷理18)如图,圆柱 内有一个三棱柱
内有一个三棱柱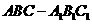 ,三棱柱的底面为圆柱底面的内接三角形,且
,三棱柱的底面为圆柱底面的内接三角形,且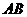 是圆
是圆 的直径。
的直径。
(Ⅰ)证明:平面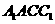 ⊥平面
⊥平面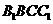 ;
;
(Ⅱ)设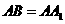 。在圆柱
。在圆柱 内随机选取一点,记该点取自于三棱柱
内随机选取一点,记该点取自于三棱柱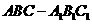 内的概率为
内的概率为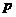 。
。
(ⅰ)当点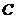 在圆周上运动时,求
在圆周上运动时,求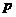 的最大值;
的最大值;
(ⅱ)记平面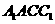 与平面
与平面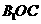 所成的角为
所成的角为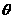 (0°<
(0°<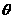 ≤90°)。当
≤90°)。当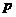 取最大值时,求
取最大值时,求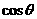 的值。
的值。
[命题意图]本小题主要考查直线与直线、直线与平面、平面与平面的位置关系,以及几何体的体积、几何概型等基础知识,考查空间想象能力、运算求解能力、推理论证能力,考查数形结合思想、化归与转化思想、必然与或然思想。
[解析](Ⅰ)因为
 平面ABC,
平面ABC,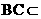 平面ABC,所以
平面ABC,所以

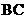 ,
,
因为AB是圆O直径,所以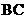

 ,又
,又
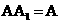 ,所以
,所以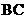
 平面
平面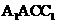 ,
,
而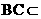 平面
平面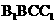 ,所以平面
,所以平面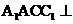 平面
平面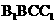 。
。
(Ⅱ)(i)设圆柱的底面半径为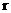 ,则AB=
,则AB=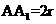 ,故三棱柱
,故三棱柱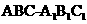 的体积为
的体积为
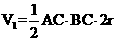 =
=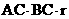 ,又因为
,又因为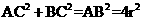 ,
,
所以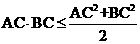 =
=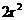 ,当且仅当
,当且仅当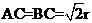 时等号成立,
时等号成立,
从而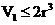 ,而圆柱的体积
,而圆柱的体积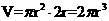 ,
,
故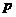 =
=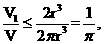 当且仅当
当且仅当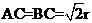 ,即
,即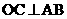 时等号成立,
时等号成立,
所以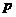 的最大值是
的最大值是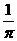 。
。
(ii)由(i)可知,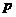 取最大值时,
取最大值时,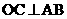 ,于是以O为坐标原点,建立空间直角坐标系
,于是以O为坐标原点,建立空间直角坐标系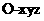 (如图),则C(r,0,0),B(0,r,0),
(如图),则C(r,0,0),B(0,r,0),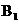 (0,r,2r),
(0,r,2r),
因为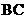
 平面
平面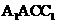 ,所以
,所以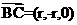 是平面
是平面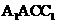 的一个法向量,
的一个法向量,
设平面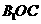 的法向量
的法向量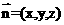 ,由
,由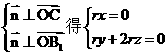 ,故
,故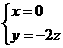 ,
,
取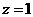 得平面
得平面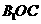 的一个法向量为
的一个法向量为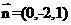 ,因为
,因为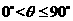 ,
,
所以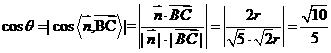 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com