
题目列表(包括答案和解析)
4. (北京卷文1)集合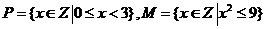 ,则
,则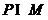 =
=
(A) {1,2} (B) {0,1,2} (C){1,2,3} (D){0,1,2,3}

3.(北京卷理1)集合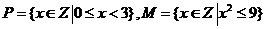 ,则
,则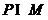 =
=
(A) {1,2} (B) {0,1,2} (C){x|0≤x<3} (D) {x|0≤x≤3}
解析: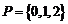 ,
,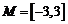 ,因此
,因此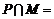
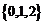
2.(安徽卷文1)若A=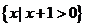 ,B=
,B=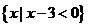 ,则
,则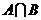 =
=
(A)(-1,+∞) (B)(-∞,3) (C)(-1,3) (D)(1,3)
[解析]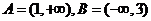 ,
,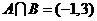 ,故选C.
,故选C.
[方法总结]先求集合A、B,然后求交集,可以直接得结论,也可以借助数轴得交集.
1.(安徽卷理2)若集合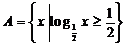 ,则
,则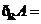
A、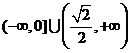 B、
B、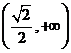 C、
C、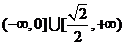 D、
D、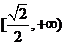
[答案]A

2.(全国Ⅰ新卷理24文24)设函数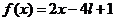
(Ⅰ)画出函数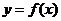 的图像
的图像
(Ⅱ)若不等式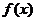 ≤
≤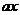 的解集非空,求a的取值范围。
的解集非空,求a的取值范围。
解:(Ⅰ)由于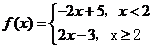 则函数
则函数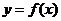 的图像如图所示。
的图像如图所示。
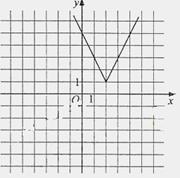 (Ⅱ)由函数
(Ⅱ)由函数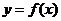 与函数
与函数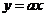 的图像可知,当且仅当
的图像可知,当且仅当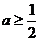 或
或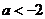 时,函数
时,函数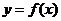 与函数
与函数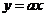 的图像有交点。故不等式
的图像有交点。故不等式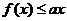 的解集非空时,
的解集非空时,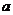 的取值范围为
的取值范围为
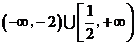 。
。
1.(福建卷理21③)已知函数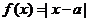 。
。
(Ⅰ)若不等式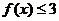 的解集为
的解集为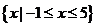 ,求实数
,求实数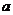 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,若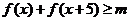 对一切实数x恒成立,求实数m的取值范围。
对一切实数x恒成立,求实数m的取值范围。
[命题意图]本小题主要考查绝对值的意义、绝对值不等式等基础知识,考查运算求解能力。
[解析](Ⅰ)由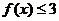 得
得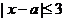 ,解得
,解得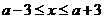 ,
,
又已知不等式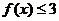 的解集为
的解集为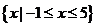 ,所以
,所以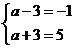 ,解得
,解得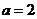 。
。
(Ⅱ)当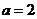 时,
时,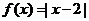 ,设
,设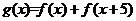 ,于是
,于是
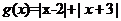 =
=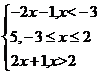 ,所以当
,所以当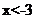 时,
时,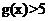 ;当
;当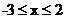 时,
时,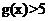 ;当
;当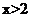 时,
时,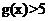 。
。
2.(陕西卷文15A)不等式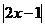 <3的解集为
.
<3的解集为
.
[答案]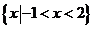
1.(陕西卷理15A)不等式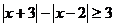 的解集为
的解集为 .
.
[答案]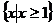
[解析](方法一)当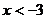 时,∵原不等式即为
时,∵原不等式即为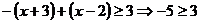 ,这显然不可能,∴
,这显然不可能,∴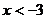 不适合.
不适合.
当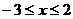 时,∵原不等式即为
时,∵原不等式即为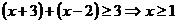 ,又
,又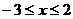 ,∴
,∴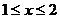 适合.
适合.
当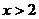 时,∵原不等式即为
时,∵原不等式即为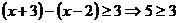 ,这显然恒成立,∴
,这显然恒成立,∴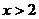 适合.
适合.
 故综上知,不等式的解集为
故综上知,不等式的解集为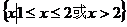 ,即
,即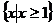 .
.
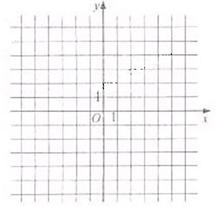
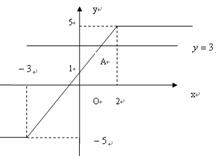
(方法二)设函数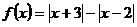 ,则
,则
∵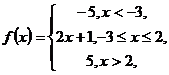 ∴作函数
∴作函数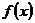
的图象,如图所示,并作直线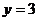 与之交于点
与之交于点 .
.
又令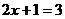 ,则
,则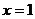 ,即点
,即点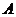 的横坐标为
的横坐标为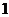 .
.
故结合图形知,不等式的解集为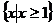 .
.
6.(重庆卷文12)已知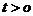 ,则函数
,则函数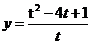 的最小值为
的最小值为
[答案]-2
[解析]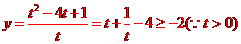 ,当且仅当
,当且仅当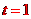 时,
时,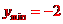 .
.
5.(浙江卷文15)若正实数x,y 满足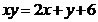 ,则xy 的最小值是 。
,则xy 的最小值是 。
解析:运用基本不等式,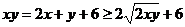 ,令
,令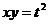 ,可得
,可得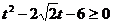 ,注意到t>0,解得t≥
,注意到t>0,解得t≥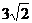 ,故xy的最小值为18,本题主要考察了用基本不等式解决最值问题的能力 ,以及换元思想和简单一元二次不等式的解法,属中档题
,故xy的最小值为18,本题主要考察了用基本不等式解决最值问题的能力 ,以及换元思想和简单一元二次不等式的解法,属中档题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com