
题目列表(包括答案和解析)
4.(2010浙江理数)(4)设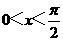 ,则“
,则“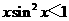 ”是“
”是“ ”的
”的

 w_w w. k#s5_
w_w w. k#s5_
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
答案:B
解析:因为0<x<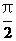 ,所以sinx<1,故xsin2x<xsinx,结合xsin2x与xsinx的取值范围相同,可知答案选B,本题主要考察了必要条件、充分条件与充要条件的意义,以及转化思想和处理不等关系的能力,属中档题
,所以sinx<1,故xsin2x<xsinx,结合xsin2x与xsinx的取值范围相同,可知答案选B,本题主要考察了必要条件、充分条件与充要条件的意义,以及转化思想和处理不等关系的能力,属中档题
3.(2010浙江理数)(9)设函数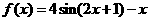 ,则在下列区间中函数
,则在下列区间中函数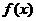 不存在零点的是
不存在零点的是

 w_w w. k#s5_
w_w w. k#s5_
(A)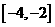 (B)
(B)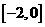 (C)
(C)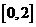 (D)
(D)
答案:A
解析:将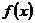 的零点转化为函数
的零点转化为函数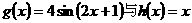 的交点,数形结合可知答案选A,本题主要考察了三角函数图像的平移和函数与方程的相关知识点,突出了对转化思想和数形结合思想的考察,对能力要求较高,属较难题
的交点,数形结合可知答案选A,本题主要考察了三角函数图像的平移和函数与方程的相关知识点,突出了对转化思想和数形结合思想的考察,对能力要求较高,属较难题
2.(2010湖南文数)7.在△ABC中,角A,B,C所对的边长分别为a,b,c,若∠C=120°,c=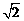 a,则
a,则
A.a>b B.a<b
C. a=b D.a与b的大小关系不能确定
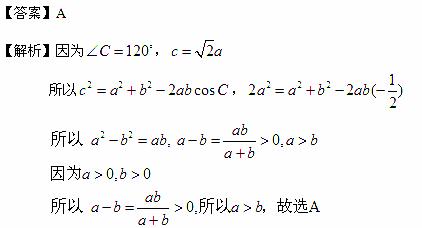
[命题意图]本题考查余弦定理,特殊角的三角函数值,不等式的性质,比较法,属中档题。
1.(2010上海文数)18.若△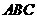 的三个内角满足
的三个内角满足 ,则△
,则△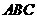
(A)一定是锐角三角形. (B)一定是直角三角形.
(C)一定是钝角三角形. (D)可能是锐角三角形,也可能是钝角三角形.
答案:C
解析:由 及正弦定理得a:b:c=5:11:13
及正弦定理得a:b:c=5:11:13
由余弦定理得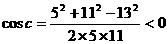 ,所以角C为钝角
,所以角C为钝角
23.(2010福建理数)3.设等差数列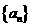 的前n项和为
的前n项和为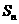 ,若
,若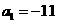 ,
,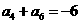 ,则当
,则当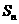 取最小值时,n等于
取最小值时,n等于

 w_w w. k#s5_
w_w w. k#s5_
A.6 B.7 C.8 D.9
[答案]A
[解析]设该数列的公差为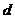 ,则
,则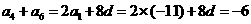 ,解得
,解得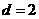 ,
,
所以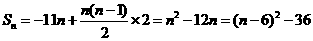 ,所以当
,所以当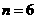 时,
时,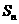 取最小值。
取最小值。
[命题意图]本题考查等差数列的通项公式以及前n项和公式的应用,考查二次函数最值的求法及计算能力。
22.(2010湖北理数)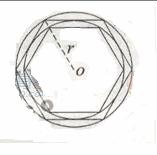 7、如图,在半径为r 的园内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设
7、如图,在半径为r 的园内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设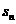 为前n个圆的面积之和,则
为前n个圆的面积之和,则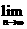
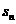 =
= 

 w_w w. k#s5_
w_w w. k#s5_
A. 2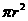 B.
B. 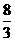
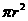 C.4
C.4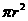 D.6
D.6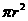

21.(2010安徽理数)10、设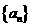 是任意等比数列,它的前
是任意等比数列,它的前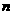 项和,前
项和,前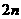 项和与前
项和与前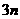 项和分别为
项和分别为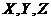 ,则下列等式中恒成立的是
,则下列等式中恒成立的是

 w_w w. k#s5_
w_w w. k#s5_
A、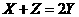 B、
B、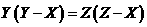
C、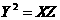 D、
D、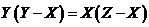
[答案]D
[分析]取等比数列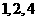 ,令
,令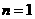 得
得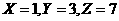 代入验算,只有选项D满足。
代入验算,只有选项D满足。
[方法技巧]对于含有较多字母的客观题,可以取满足条件的数字代替字母,代入验证,若能排除3个选项,剩下唯一正确的就一定正确;若不能完全排除,可以取其他数字验证继续排除.本题也可以首项、公比即项数n表示代入验证得结论.
20.(2010山东理数)

19.(2010湖北文数)7.已知等比数列{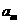 }中,各项都是正数,且
}中,各项都是正数,且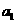 ,
,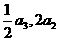 成等差数列,则
成等差数列,则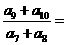
A.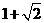 B.
B.
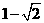 C.
C.
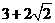 D
D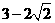


 w_w w. k#s5_
w_w w. k#s5_
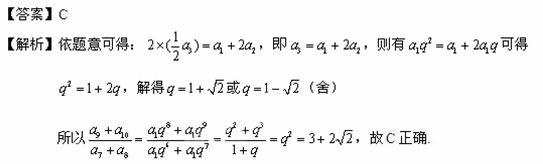
18.(2010全国卷1理数)(4)已知各项均为正数的等比数列{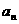 }中,
}中,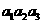 =5,
=5,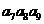 =10,则
=10,则
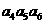 =
=

 w_w w. k#s5_
w_w w. k#s5_
(A) 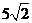 (B) 7 (C) 6 (D)
(B) 7 (C) 6 (D) 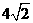

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com