
题目列表(包括答案和解析)
5.(湖北卷理16)已知函数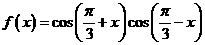 ,
,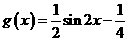 .
.
(Ⅰ)求函数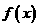 的最小正周期;
的最小正周期;
(Ⅱ)求函数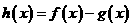 的最大值,并求使
的最大值,并求使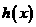 取得最大值的
取得最大值的 的集合.
的集合.

4.(广东卷文16)设函数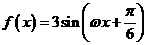 ,
,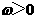 ,
,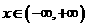 ,且以
,且以 为最小正周期.
为最小正周期.
(1)求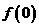 ;
;
(2)求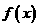 的解析式;
的解析式;
(3)已知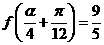 ,求
,求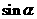 的值.w_w
的值.w_w
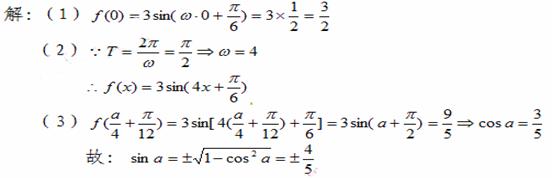
3. (广东卷理16)已知函数
(广东卷理16)已知函数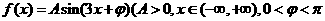 在
在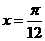 时取得最大值4.
时取得最大值4.
(1) 求 的最小正周期;
的最小正周期;
(2) 求 的解析式;
的解析式;
(3) 若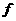 (
(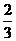 α +
α +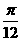 )=
)=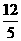 ,求sinα.
,求sinα.

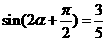 ,
,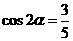 ,
,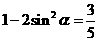 ,
,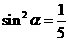 ,
,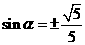 .
.
2.(北京卷文15)已知函数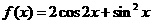
(Ⅰ)求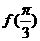 的值;
的值;
(Ⅱ)求 的最大值和最小值
的最大值和最小值
1.(北京卷理15)已知函数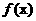
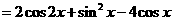 。
。
(Ⅰ)求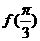 的值;
的值;
(Ⅱ)求 的最大值和最小值。
的最大值和最小值。
解析:(I)
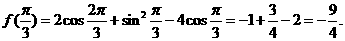
(2)
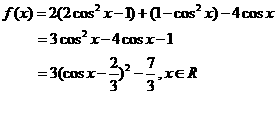
因为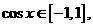 所以当
所以当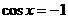 时,
时, 取最大值6;当
取最大值6;当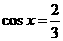 时,取最小值
时,取最小值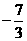 。
。
5.(上海春卷1)函数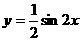 的最小正周期T=_______________。
的最小正周期T=_______________。
答案: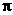
解析:由周期公式得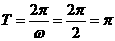 。
。
4.(浙江卷文12)函数 的最小正周期是
。
的最小正周期是
。
解析:对解析式进行降幂扩角,转化为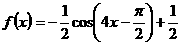 ,可知其最小正周期为
,可知其最小正周期为 ,本题主要考察了二倍角余弦公式的灵活运用,属容易题。
,本题主要考察了二倍角余弦公式的灵活运用,属容易题。
3.(浙江卷理11)函数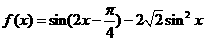 的最小正周期是_________ .
的最小正周期是_________ .
解析: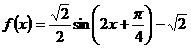 故最小正周期为π,本题主要考察了三角恒等变换及相关公式,属中档题
故最小正周期为π,本题主要考察了三角恒等变换及相关公式,属中档题
2.(江苏卷10)定义在区间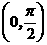 上的函数y=6cosx的图像与y=5tanx的图像的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx的图像交于点P2,则线段P1P2的长为_____。
上的函数y=6cosx的图像与y=5tanx的图像的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx的图像交于点P2,则线段P1P2的长为_____。
[答案]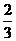
[解析] 考查三角函数的图象、数形结合思想。线段P1P2的长即为sinx的值,
且其中的x满足6cosx=5tanx,解得sinx=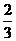 。线段P1P2的长为
。线段P1P2的长为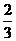
1.(福建卷理14)已知函数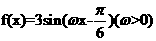 和
和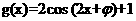 的图象的对称轴完全相同。若
的图象的对称轴完全相同。若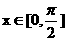 ,则
,则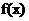 的取值范围是
。
的取值范围是
。
[答案]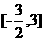
[解析]由题意知, ,因为
,因为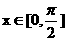 ,所以
,所以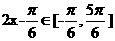 ,由三角函数图象知:
,由三角函数图象知:
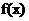 的最小值为
的最小值为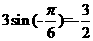 ,最大值为
,最大值为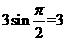 ,所以
,所以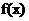 的取值范围是
的取值范围是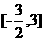 。
。
[命题意图]本题考查三角函数的图象与性质,考查了数形结合的数学思想。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com