
题目列表(包括答案和解析)
6.(辽宁卷理18)为了比较注射A, B两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物A,另一组注射药物B。
(Ⅰ)甲、乙是200只家兔中的2只,求甲、乙分在不同组的概率;
(Ⅱ)下表1和表2分别是注射药物A和B后的试验结果.(疱疹面积单位:mm2)
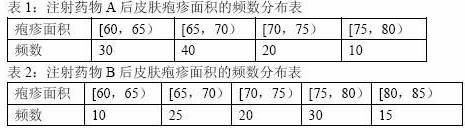
(ⅰ)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;
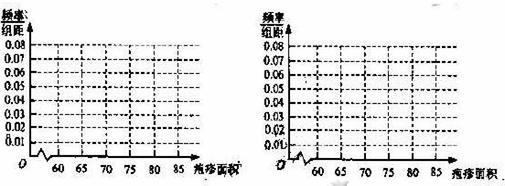
(ⅱ)完成下面2×2列联表,并回答能否有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”.
表3:

解:(Ⅰ)甲、乙两只家兔分在不同组的概率为
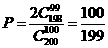 ……4分
……4分
(Ⅱ)(i)
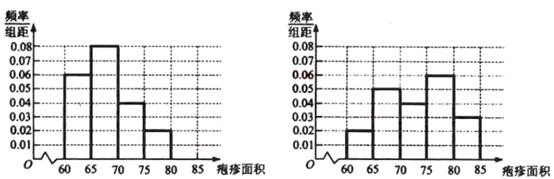
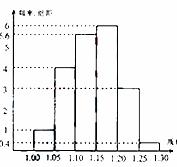
图Ⅰ注射药物A后皮肤疱疹面积的频率分布直方图 图Ⅱ注射药物B后皮肤疱疹面积的频率分布直方图
可以看出注射药物A后的疱疹面积的中位数在65至70之间,而注射药物B后的疱疹面积的中位数在70至75之间,所以注射药物A后疱疹面积的中位数小于注射药物B后疱疹面积的中位数。 ……8分
(ii)表3:
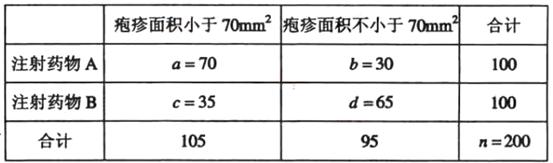
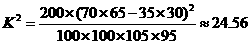
由于K2>10.828,所以有99.9%的把握认为“注射药物A后的疱疹面积于注射药物B后的疱疹面积有差异”。

5.(江西卷文18)某迷宫有三个通道,进入迷宫的每个人都要经过一扇智能门。首次到达此门,系统会随机(即等可能)为你打开一个通道.若是1号通道,则需要1小时走出迷宫;若是2号、3号通道,则分别需要2小时、3小时返回智能门.再次到达智能门时,系统会随机打开一个你未到过的通道,直至走出迷宫为止.
(1)求走出迷宫时恰好用了1小时的概率;
(2)求走出迷宫的时间超过3小时的概率.
解:(1)设A表示走出迷宫时恰好用了1小时这一事件,则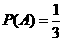 .
.
(2) 设B表示走出迷宫的时间超过3小时这一事件,则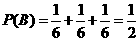 .
.
4.(江苏卷22)某厂生产甲、乙两种产品,生产甲产品一等品80%,二等品20%;生产乙产品,一等品90%,二等品10%。生产一件甲产品,如果是一等品可获利4万元,若是二等品则要亏损1万元;生产一件乙产品,如果是一等品可获利6万元,若是二等品则要亏损2万元。设生产各种产品相互独立
记x(单位:万元)为生产1件甲产品和件乙产品可获得的总利润,求x的分布列
求生产4件甲产品所获得的利润不少于10万元的概率
[解析] 本题主要考查概率的有关知识,考查运算求解能力。满分10分。
解:(1)由题设知,X的可能取值为10,5,2,-3,且
P(X=10)=0.8×0.9=0.72, P(X=5)=0.2×0.9=0.18,
P(X=2)=0.8×0.1=0.08, P(X=-3)=0.2×0.1=0.02。
由此得X的分布列为:
|
X |
10 |
5 |
2 |
-3 |
|
P |
0.72 |
0.18 |
0.08 |
0.02 |
(2)设生产的4件甲产品中一等品有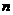 件,则二等品有
件,则二等品有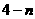 件。
件。
由题设知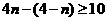 ,解得
,解得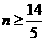 ,
,
又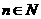 ,得
,得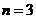 ,或
,或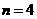 。
。
所求概率为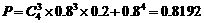
答:生产4件甲产品所获得的利润不少于10万元的概率为0.8192。
3.(湖南卷文17)为了对某课题进行研究,用分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组、有关数据见下表(单位:人)
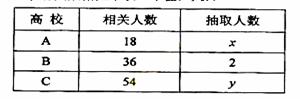
(Ⅰ)求x,y ;
(Ⅱ)若从高校B、C抽取的人中选2人作专题发言,求这二人都来自高校C的概率。


2. (广东卷文17)某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
(广东卷文17)某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:

 (1)由表中数据直观分析,收看新闻节目的观众是否与年龄有关?
(1)由表中数据直观分析,收看新闻节目的观众是否与年龄有关?
(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?
(3)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率。

1.(福建卷文18)设平面向量a m =(m,1),b n =(2,n),其中m,n∈{1,2,3,4}.
(I)请列出有序数组(m,n)的所有可能结果;
(II)记“使得a m ⊥(a m-b n)成立的(m,n)”为事件A,求事件A发生的概率.
13.(上海春卷9)连续两次掷骰子,出现点数之和等于4的概率为____________(结果用数值表示)。
答案: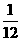 。解析:点数和为的结果为(1,3),(2,2),(3,1)共3个,而总的试验结果为36个,由古典概型概率计算公式可得
。解析:点数和为的结果为(1,3),(2,2),(3,1)共3个,而总的试验结果为36个,由古典概型概率计算公式可得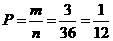 。
。
12.(重庆卷文14)加工某一零件需经过三道工序,设第一、二、三道工序的次品率分别为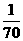 、
、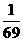 、
、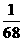 ,且各道工序互不影响,则加工出来的零件的次品率为
。
,且各道工序互不影响,则加工出来的零件的次品率为
。
[答案]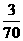
[解析]加工出来的零件的次品的对立事件为零件是正品,由对立事件公式得加工出来的零件的次品率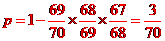 .
.
11.(重庆卷理13)某篮球队员在比赛中每次罚球的命中率相同,且在两次罚球中至多命中一次的概率为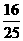 ,则该队员每次罚球的命中率为____________.
,则该队员每次罚球的命中率为____________.
[答案]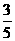
解析:由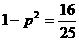 得
得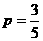
10.(浙江卷文17)在平行四边形ABCD中,O是AC与BD的交点,P、Q、M、N分别是线段OA、OB、OC、OD的中点,在APMC中任取一点记为E,在B、Q、N、D中任取一点记为F,设G为满足向量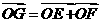 的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为
。
的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为
。
解析:由题意知,G点共有16种取法,而只有E为P、M中一点,F为Q、N中一点时,落在平行四边形内,故符合要求的G的只有4个,因此概率为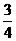 ,本题主要考察了平面向量与古典概型的综合运用,属中档题
,本题主要考察了平面向量与古典概型的综合运用,属中档题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com