(二)主要方法：

1．涉及等差(比)数列的基本概念的问题，常用基本量来处理；

2．使用等比数列前项和公式时，必须弄清公比是否可能等于1还是必不等于1，如果不能确定则需要讨论；

3．若奇数个成等差数列且和为定值时，可设中间三项为；若偶数个成等差数列且和为定值时，可设中间两项为，其余各项再根据等差数列的定义进行对称设元．若干个数个成等比数列且积为定值时，设元方法与等差数列类似．

4．在求解数列问题时要注意运用函数思想，方程思想和整体消元思想，设而不求．

(一)主要知识：

1．等差数列的概念及其通项公式，等差数列前项和公式；

2．等比数列的概念及其通项公式，等比数列前项和公式；

3．等差中项和等比中项的概念．

版权所有：()

版权所有：()

(四)巩固练习：

1．若数列(*)是等差数列，则有数列(*)也为等差数列，类比上述性质，相应地：若数列是等比数列，且(*)，则有(*)也是等比数列．

2．设和分别为两个等差数列的前项和，若对任意，都有 ，则第一个数列的第项与第二个数列的第项的比是．

说明：．　

(三)例题分析：

例1．(1)若一个等差数列前3项的和为34，最后三项的和为146，且所有项的和为,则这个数列有13 项；

(2)已知数列是等比数列,且,,，则　 9　 ．

(3)等差数列前项和是，前项和是，则它的前项和是 210 ．

例2．若数列成等差数列，且，求．

解：(法一)基本量法(略)；

　 (法二)设，则

得：，， ∴，

∴．

例3．等差数列中共有奇数项，且此数列中的奇数项之和为，偶数项之和为，，求其项数和中间项.

解：设数列的项数为项，

则，

∴，∴，∴数列的项数为，中间项为第项，且．

说明：

(1)在项数为项的等差数列中，；

(2)在项数为项的等差数列中．

例4．数列是首项为，公比为的等比数列，数列满足

　 ，

(1)求数列的前项和的最大值；(2)求数列的前项和．

解：(1)由题意：，∴，

∴数列是首项为3，公差为的等差数列，

∴，∴

由，得，∴数列的前项和的最大值为

(2)由(1)当时，，当时，，

∴当时，

当时，

∴．

例5*．若和分别表示数列和的前项和，对任意自然数，有，，(1)求数列的通项公式；(2)设集合，

．若等差数列任一项是中的最大数，且，求的通项公式．

解：(1)当时：，

两式相减得：，∴，又也适合上式，

∴数列的通项公式为．

(2)对任意，，∴，∴

∵是中的最大数，∴，设等差数列的公差为，则，

∴，即，又是一个以为公差的等差数列，

∴，∴，∴．

(二)主要方法：

1．解决等差数列和等比数列的问题时，通常考虑两类方法：①基本量法：即运用条件转化为关于和的方程；②巧妙运用等差数列和等比数列的性质，一般地运用性质可以化繁为简，减少运算量．

2．深刻领会两类数列的性质，弄清通项和前项和公式的内在联系是解题的关键．

(一)主要知识：

有关等差、等比数列的结论

1．等差数列的任意连续项的和构成的数列仍为等差数列．

2．等差数列中，若，则

3．等比数列中，若，则

4．等比数列{a_n}的任意连续项的和构成的数列仍为等比数列．

5．两个等差数列与的和差的数列仍为等差数列．

6．两个等比数列与的积、商、倒数的数列、、仍为等比数列．

(四)巩固练习：

1．的解集是；的解集是；

2．不等式成立的充要条件是；

3．若关于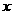的不等式的解集不是空集，则；

4．不等式成立，则

版权所有：()

版权所有：()

(三)例题分析：

例1．解下列不等式：

(1)；(2)；(3)．

解：(1)原不等式可化为或，∴原不等式解集为．

(2)原不等式可化为，即，∴原不等式解集为．

(3)当时，原不等式可化为，∴，此时；

当时，原不等式可化为，∴，此时；

当时，原不等式可化为，∴，此时．

综上可得：原不等式的解集为．

例2．(1)对任意实数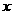，恒成立，则的取值范围是；

(2)对任意实数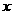，恒成立，则的取值范围是．

解：(1)可由绝对值的几何意义或的图象或者绝对值不等式的性质得，∴；

(2)与(1)同理可得，∴．

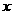例3．(《高考计划》考点3“智能训练第13题”)设，解关于的不等式：．

解：原不等式可化为或，即①或②，

当时，由①得，∴此时，原不等式解为：或；

当时，由①得，∴此时，原不等式解为：；

当时，由①得，∴此时，原不等式解为：．

综上可得，当时，原不等式解集为，

当时，原不等式解集为．

例4．已知，，且，求实数的取值范围．

解：当时，，此时满足题意；

当时，，∵，

∴，

综上可得，的取值范围为．

例5．(《高考计划》考点3“智能训练第15题”)在一条公路上，每隔有个仓库(如下图)，共有5个仓库．一号仓库存有货物，二号仓库存，五号仓库存，其余两个仓库是空的．现在想把所有的货物放在一个仓库里，如果每吨货物运输需要元运输费，那么最少要多少运费才行？

解：以一号仓库为原点建立坐标轴，

则五个点坐标分别为，

设货物集中于点，则所花的运费，

当时，，此时，当时，；

当时，，此时，；

当时，，此时，当时，．

综上可得，当时，，即将货物都运到五号仓库时，花费最少，为元．

(二)主要方法：

1．解含绝对值的不等式的基本思想是去掉绝对值符号，将其等价转化为一元一次(二次)不等式(组)进行求解；

2．去掉绝对值的主要方法有：

(1)公式法：，或．

(2)定义法：零点分段法；

(3)平方法：不等式两边都是非负时，两边同时平方．