
题目列表(包括答案和解析)
(三)基础训练:
1.下列个命题中,真命题的个数为 ( )
①若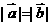 ,则
,则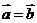 或
或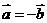 ②若
②若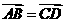 ,则
,则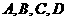 是一个平行四边形的四个顶点 ③若
是一个平行四边形的四个顶点 ③若 ,则
,则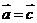 ④若
④若 ,则
,则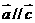
 4
4
 3
3
 2
2  1
1
2.在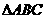 中,已知
中,已知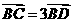 ,则
,则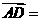 (
)
(
)
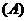
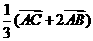
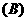
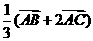

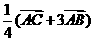
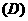
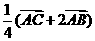
3.化简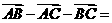 。
。
4.边长为1的正方形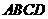 中,设
中,设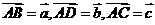 ,则
,则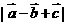 = 。
= 。
5.下面三种说法:
①一个平面内只有一对不共线向量可作为表示该平面所有向量的基底;
②一个平面内有无数多对不共线向量可作为表示该平面所有向量的基底;
③零向量不可为基底中的向量。 其中正确的说法是:( )
A.①,②;B.②,③;C.①,③;D.①,②,③。
 (四)例题分析:
(四)例题分析:
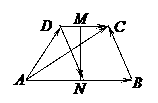
例1.已知梯形 中,
中,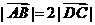 ,
, ,
, 分别是
分别是 、
、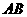 的中点,若
的中点,若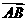
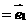 ,
,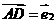 ,用
,用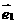 ,
,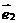 表示
表示 、
、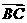 、
、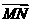 .
.
解:(1)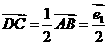
(2)
(3)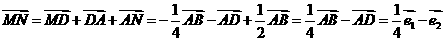
例2.(1)设两个非零向量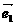 、
、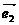 不共线,如果
不共线,如果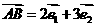 ,
,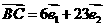
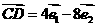 ,求证:
,求证: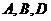 三点共线.
三点共线.
(2)设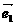 、
、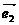 是两个不共线的向量,已知
是两个不共线的向量,已知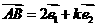 ,
,
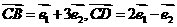 ,若
,若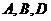 三点共线,求
三点共线,求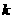 的值.
的值.
(1)证明:因为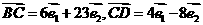
所以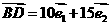 ,又因为
,又因为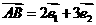 ,得
,得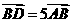
即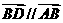 ,又因为公共点
,又因为公共点 ,所以
,所以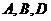 三点共线;
三点共线;
(2)解: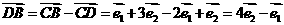
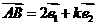 ,因为
,因为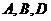 共线,所以
共线,所以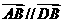
设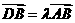 ,所以
,所以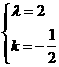 即
即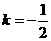 ;
;
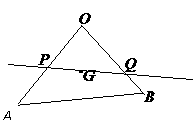 例3. 经过
例3. 经过 重心
重心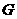 的直线与
的直线与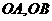 分别交于点
分别交于点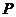 ,
,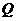 ,
,
设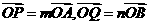 ,
,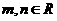 ,求
,求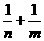 的值。
的值。
解:设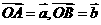 ,则
,则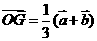 ,
,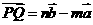

由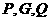 共线,得
共线,得
存在实数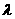 ,使得
,使得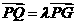 ,即
,即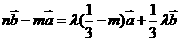
从而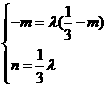 ,消去
,消去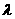 得:
得: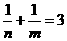
(二)主要方法:
1.充分理解向量的概念和向量的表示;
2.数形结合的方法的应用;
3.用基底向量表示任一向量唯一性;
4.向量的特例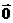 和单位向量,要考虑周全.
和单位向量,要考虑周全.
(一)主要知识:
1.向量的概念及向量的表示;
2.向量的加法、减法与实数乘向量概念与运算律;
3.两向量共线定理与平面向量基本定理.
2.会用向量的代数运算法则、三角形法则、平行四边形法则解决有关问题.不断培养并深化用数形结合的思想方法解题的自觉意识.
12.已知平行四边形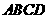 中,点
中,点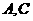 的坐标分别是
的坐标分别是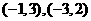 ,点
,点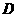 在椭圆
在椭圆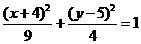 上移动,求
上移动,求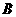 点的轨迹方程
点的轨迹方程
|

|
版权所有:()
版权所有:()
11.向量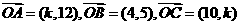 ,当
,当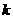 为何值时,
为何值时,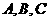 三点共线?
三点共线?
10.已知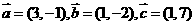 ,求
,求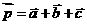 ,并以
,并以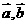 为基底来表示
为基底来表示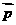 。
。
9.已知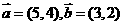 ,则与
,则与 平行的单位向量的坐标为 。
平行的单位向量的坐标为 。
8.已知向量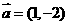 ,
,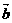 与
与 方向相反,且
方向相反,且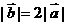 ,那么向量
,那么向量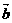 的坐标是 .
的坐标是 .
7.如果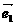 ,
, 是平面
是平面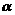 内所有向量的一组基底,那么下列命题中正确的是( )
内所有向量的一组基底,那么下列命题中正确的是( )
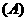 若实数
若实数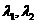 使
使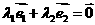 ,则
,则 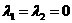
 空间任一向量
空间任一向量 可以表示为
可以表示为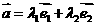 ,这里
,这里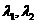 是实数
是实数
 对实数
对实数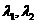 ,向量
,向量 不一定在平面
不一定在平面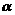 内
内
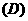 对平面内任一向量
对平面内任一向量 ,使
,使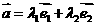 的实数
的实数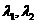 有无数对
有无数对
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com