
题目列表(包括答案和解析)
2.(北京卷文6)给定函数①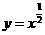 ,②
,②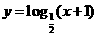 ,③
,③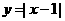 ,④
,④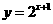 ,期中在区间(0,1)上单调递减的函数序号是
,期中在区间(0,1)上单调递减的函数序号是
(A)①② (B)②③ (C)③④ (D)①④
1.(安徽卷理4)若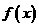 是
是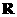 上周期为5的奇函数,且满足
上周期为5的奇函数,且满足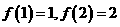 ,则
,则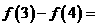
A、-1 B、1 C、-2 D、2
[答案]A

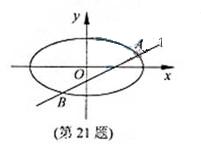
19.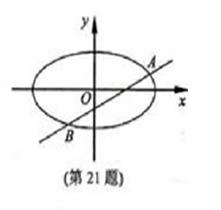 (天津卷文21)已知椭圆
(天津卷文21)已知椭圆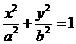 (a>b>0)的离心率e=
(a>b>0)的离心率e=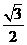 ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线l与椭圆相交于不同的两点A、B,已知点A的坐标为(-a,0).
(i)若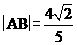 ,求直线l的倾斜角;
,求直线l的倾斜角;
(ii)若点Q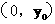 在线段AB的垂直平分线上,且
在线段AB的垂直平分线上,且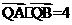 .求
.求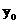 的值.
的值.
[命题意图]本小题主要考查椭圆的标准方程和几何性质、直线的方程、两点间的距离公式、直线的倾斜角、平面向量等基础知识,考查用代数方法研究圆锥曲线的性质及数形结合的思想,考查综合分析与运算能力.
[解析](Ⅰ)解:由e=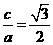 ,得
,得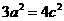 .再由
.再由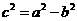 ,解得a=2b.
,解得a=2b.
由题意可知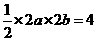 ,即ab=2.
,即ab=2.
解方程组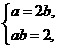 得a=2,b=1,所以椭圆的方程为
得a=2,b=1,所以椭圆的方程为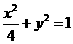 .
.
(Ⅱ)(i)解:由(Ⅰ)可知点A的坐标是(-2,0).设点B的坐标为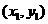 ,直线l的斜率为k.则直线l的方程为y=k(x+2).
,直线l的斜率为k.则直线l的方程为y=k(x+2).
于是A、B两点的坐标满足方程组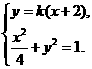 消去y并整理,得
消去y并整理,得
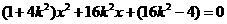 .
.
由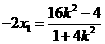 ,得
,得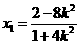 .从而
.从而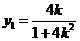 .
.
所以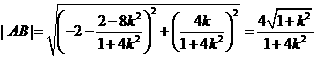 .
.
由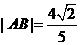 ,得
,得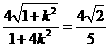 .
.
整理得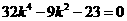 ,即
,即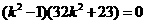 ,解得k=
,解得k=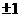 .
.
所以直线l的倾斜角为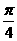 或
或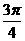 .
.
(ii)解:设线段AB的中点为M,由(i)得到M的坐标为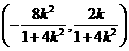 .
.
以下分两种情况:
(1)当k=0时,点B的坐标是(2,0),线段AB的垂直平分线为y轴,于是
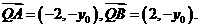 由
由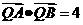 ,得
,得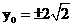 。
。
(2)当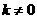 时,线段AB的垂直平分线方程为
时,线段AB的垂直平分线方程为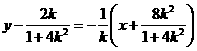 。
。
令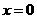 ,解得
,解得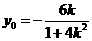 。
。
由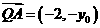 ,
,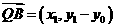 ,
,
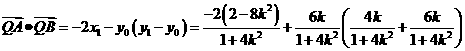
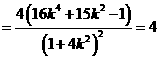 ,
,
整理得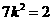 。故
。故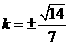 。所以
。所以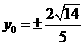 。
。
综上,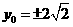 或
或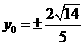
当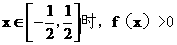 等价于
等价于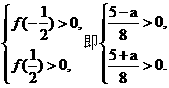
解不等式组得-5<a<5.因此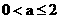 .
.
20(浙江卷理21)已知m>1,直线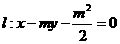 ,
,
椭圆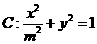 ,
,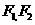 分别为椭圆
分别为椭圆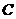 的左、右焦点.
的左、右焦点.
(Ⅰ)当直线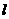 过右焦点
过右焦点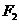 时,求直线
时,求直线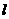 的方程;
的方程;
(Ⅱ)设直线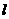 与椭圆
与椭圆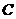 交于
交于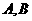 两点,
两点,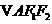 ,
,
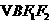 的重心分别为
的重心分别为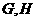 .若原点
.若原点 在以线段
在以线段
 为直径的圆内,求实数
为直径的圆内,求实数 的取值范围.
的取值范围.
解析:本题主要考察椭圆的几何性质,直线与椭圆,点与圆的位置关系等基础知识,同时考察解析几何的基本思想方法和综合解题能力。
(Ⅰ)解:因为直线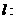
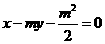 经过
经过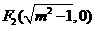 ,
,
所以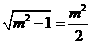 ,得
,得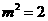 ,
,
又因为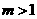 ,所以
,所以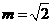 ,
,
故直线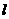 的方程为
的方程为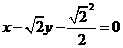 。
。
 (Ⅱ)解:设
(Ⅱ)解:设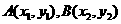 。
。
由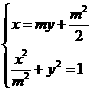 ,消去
,消去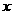 得
得
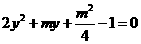
则由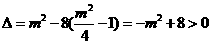 ,知
,知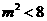 ,
,
且有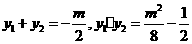 。
。
由于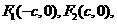 ,故
,故 为
为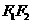 的中点,
的中点,
由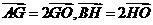 ,可知
,可知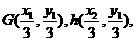
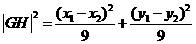
设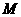 是
是 的中点,则
的中点,则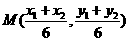 ,
,
由题意可知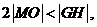
即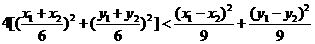 即
即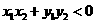
而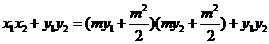
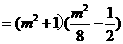
所以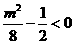 即
即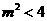
又因为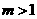 且
且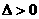 所以
所以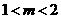 。
。
所以 的取值范围是
的取值范围是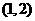 。
。
18.(天津卷理20)已知椭圆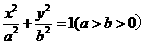 的离心率
的离心率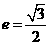 ,连接椭圆的四个顶点得到的菱形的面积为4。
,连接椭圆的四个顶点得到的菱形的面积为4。
求椭圆的方程;
设直线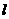 与椭圆相交于不同的两点
与椭圆相交于不同的两点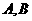 ,已知点
,已知点 的坐标为(
的坐标为(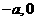 ),点
),点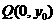 在线段
在线段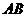 的垂直平分线上,且
的垂直平分线上,且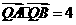 ,求
,求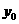 的值
的值
[命题意图]本小题主要考察椭圆的标准方程和几何性质,直线的方程,平面向量等基础知识,考查用代数方法研究圆锥曲线的性质及数形结合的思想,考查运算和推理能力。
[解析](1)解:由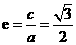 ,得
,得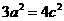 ,再由
,再由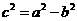 ,得
,得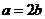
由题意可知,
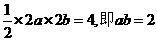
解方程组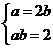 得 a=2,b=1
所以椭圆的方程为
得 a=2,b=1
所以椭圆的方程为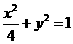
(2)解:由(1)可知A(-2,0)。设B点的坐标为(x1,,y1),直线l的斜率为k,则直线l的方程为y=k(x+2),
于是A,B两点的坐标满足方程组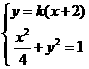
由方程组消去Y并整理,得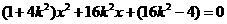
由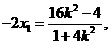 得
得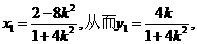
设线段AB是中点为M,则M的坐标为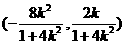
以下分两种情况:
(1)当k=0时,点B的坐标为(2,0)。线段AB的垂直平分线为y轴,于是
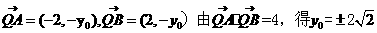
(2)当K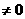 时,线段AB的垂直平分线方程为
时,线段AB的垂直平分线方程为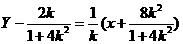
令x=0,解得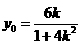
由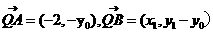
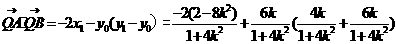
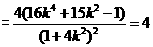
整理得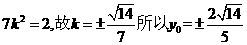
综上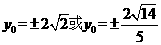 。
。
17.(上海卷文23)已知椭圆 的方程为
的方程为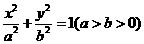 ,
,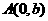 、
、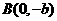 和
和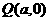 为
为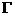 的三个顶点.
的三个顶点.
(1)若点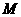 满足
满足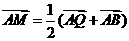 ,求点
,求点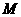 的坐标;
的坐标;
(2)设直线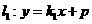 交椭圆
交椭圆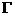 于
于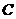 、
、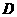 两点,交直线
两点,交直线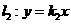 于点
于点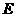 .若
.若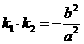 ,证明:
,证明: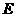 为
为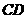 的中点;
的中点;
(3)设点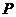 在椭圆
在椭圆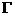 内且不在
内且不在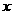 轴上,如何构作过
轴上,如何构作过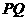 中点
中点 的直线
的直线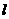 ,使得
,使得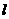 与椭圆
与椭圆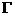 的两个交点
的两个交点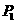 、
、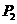 满足
满足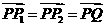 ?令
?令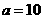 ,
,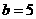 ,点
,点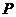 的坐标是(-8,-1),若椭圆
的坐标是(-8,-1),若椭圆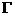 上的点
上的点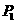 、
、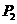 满足
满足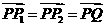 ,求点
,求点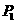 、
、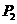 的坐标.
的坐标.
解析:(1) 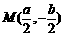 ;
(2) 由方程组
;
(2) 由方程组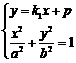 ,消y得方程
,消y得方程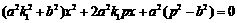 ,
因为直线
,
因为直线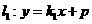 交椭圆
交椭圆 于
于 、
、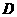 两点,所以D>0,即
两点,所以D>0,即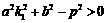 ,
设C(x1,y1)、D(x2,y2),CD中点坐标为(x0,y0),
则
,
设C(x1,y1)、D(x2,y2),CD中点坐标为(x0,y0),
则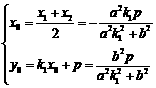 ,由方程组
,由方程组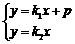 ,消y得方程(k2-k1)x=p,
又因为
,消y得方程(k2-k1)x=p,
又因为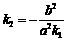 ,所以
,所以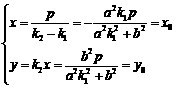 ,
故E为CD的中点;
(3) 因为点P在椭圆Γ内且不在x轴上,所以点F在椭圆Γ内,可以求得直线OF的斜率k2,由
,
故E为CD的中点;
(3) 因为点P在椭圆Γ内且不在x轴上,所以点F在椭圆Γ内,可以求得直线OF的斜率k2,由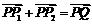 知F为P1P2的中点,根据(2)可得直线l的斜率
知F为P1P2的中点,根据(2)可得直线l的斜率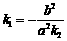 ,从而得直线l的方程.
,从而得直线l的方程.
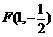 ,直线OF的斜率
,直线OF的斜率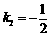 ,直线l的斜率
,直线l的斜率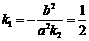 ,
解方程组
,
解方程组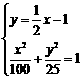 ,消y:x2-2x-48=0,解得P1(-6,-4)、P2(8,3).
,消y:x2-2x-48=0,解得P1(-6,-4)、P2(8,3).
16.(上海卷理23)已知椭圆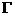 的方程为
的方程为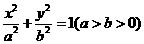 ,点P的坐标为(-a,b).
,点P的坐标为(-a,b).
(1)若直角坐标平面上的点M、A(0,-b),B(a,0)满足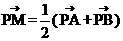 ,求点
,求点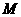 的坐标;
的坐标;
(2)设直线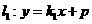 交椭圆
交椭圆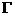 于
于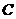 、
、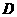 两点,交直线
两点,交直线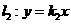 于点
于点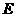 .若
.若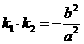 ,证明:
,证明: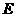 为
为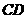 的中点;
的中点;
(3)对于椭圆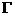 上的点Q(a cosθ,b sinθ)(0<θ<π),如果椭圆
上的点Q(a cosθ,b sinθ)(0<θ<π),如果椭圆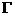 上存在不同的两个交点
上存在不同的两个交点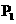 、
、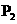 满足
满足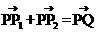 ,写出求作点
,写出求作点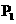 、
、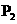 的步骤,并求出使
的步骤,并求出使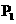 、
、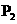 存在的θ的取值范围.
存在的θ的取值范围.
解析:(1) 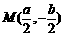 ;
(2) 由方程组
;
(2) 由方程组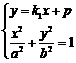 ,消y得方程
,消y得方程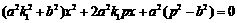 ,
因为直线
,
因为直线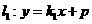 交椭圆
交椭圆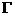 于
于 、
、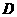 两点,所以D>0,即
两点,所以D>0,即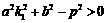 ,
设C(x1,y1)、D(x2,y2),CD中点坐标为(x0,y0),
则
,
设C(x1,y1)、D(x2,y2),CD中点坐标为(x0,y0),
则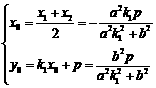 ,由方程组
,由方程组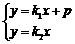 ,消y得方程(k2-k1)x=p,
又因为
,消y得方程(k2-k1)x=p,
又因为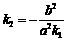 ,所以
,所以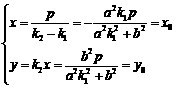 ,故E为CD的中点;
(3) 求作点P1、P2的步骤:1°求出PQ的中点
,故E为CD的中点;
(3) 求作点P1、P2的步骤:1°求出PQ的中点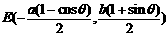 ,
2°求出直线OE的斜率
,
2°求出直线OE的斜率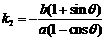 ,
3°由
,
3°由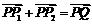 知E为CD的中点,根据(2)可得CD的斜率
知E为CD的中点,根据(2)可得CD的斜率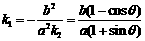 ,
4°从而得直线CD的方程:
,
4°从而得直线CD的方程: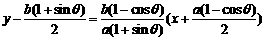 ,
5°将直线CD与椭圆Γ的方程联立,方程组的解即为点P1、P2的坐标.
欲使P1、P2存在,必须点E在椭圆内,
所以
,
5°将直线CD与椭圆Γ的方程联立,方程组的解即为点P1、P2的坐标.
欲使P1、P2存在,必须点E在椭圆内,
所以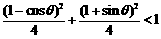 ,化简得
,化简得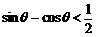 ,
,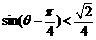 ,
又0<q <p,即
,
又0<q <p,即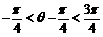 ,所以
,所以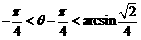 ,
故q 的取值范围是
,
故q 的取值范围是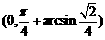 .
.
15.(陕西卷文20)如图,椭圆C: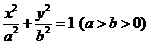 的顶点为A1,A2,B1,B2,焦点为F1,F2, | A1B1| =
的顶点为A1,A2,B1,B2,焦点为F1,F2, | A1B1| =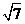 ,
,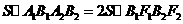
(Ⅰ)求椭圆C的方程;
(Ⅱ)设n 为过原点的直线,l是与n垂直相交与点P,与椭圆相交于A,B两点的直线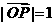 ,是否存在上述直线l使
,是否存在上述直线l使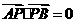 成立?若存在,求出直线l的方程;并说出;若不存在,请说明理由。
成立?若存在,求出直线l的方程;并说出;若不存在,请说明理由。


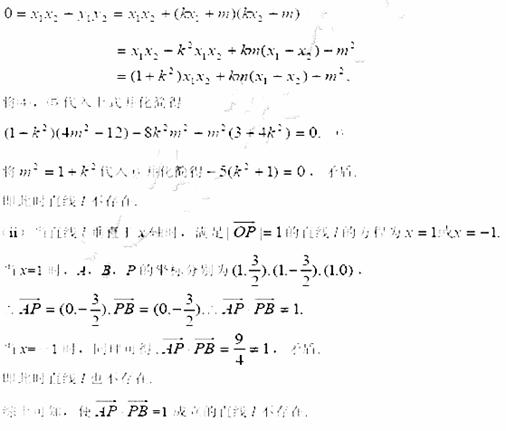
14.(陕西卷理20)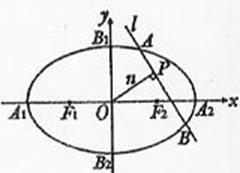 如图,椭圆C:
如图,椭圆C: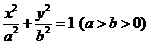 的顶点为A1,A2,B1,B2,焦点为F1,F2, | A1B1| =
的顶点为A1,A2,B1,B2,焦点为F1,F2, | A1B1| =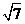 ,
,
(Ⅰ)求椭圆C的方程;
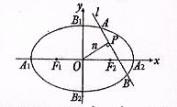 (Ⅱ)设n是过原点的直线,l是与n垂直相交于P点、与椭圆相交于A,B两点的直线,
(Ⅱ)设n是过原点的直线,l是与n垂直相交于P点、与椭圆相交于A,B两点的直线,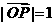 ,是否存在上述直线l使
,是否存在上述直线l使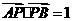 成立?若存在,求出直线l的方程;若不存在,请说明理由。
成立?若存在,求出直线l的方程;若不存在,请说明理由。



13.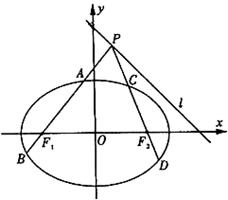 (山东卷文22)如图,已知椭圆
(山东卷文22)如图,已知椭圆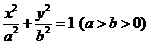 过
点.
过
点.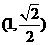 ,离心率为
,离心率为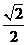 ,左、右焦点分别为
,左、右焦点分别为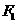 、
、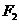 .点
.点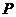 为直线
为直线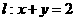 上且不在
上且不在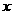 轴上的任意一点,直线
轴上的任意一点,直线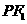 和
和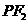 与椭圆的交点分别为
与椭圆的交点分别为 、
、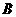 和
和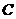 、
、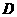 ,
, 为坐标原点.
为坐标原点.
(I)求椭圆的标准方程;
(II)设直线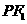 、
、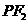 的斜线分别为
的斜线分别为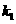 、
、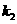 .
.
(i)证明: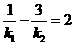 ;
;
(ii)问直线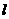 上是否存在点
上是否存在点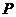 ,使得直线
,使得直线 、
、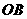 、
、 、
、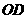 的斜率
的斜率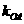 、
、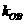 、
、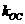 、
、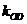 满足
满足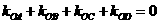 ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点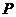 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
[命题意图]本小题主要考查椭圆的基本概念和性质,考查直线与椭圆的位置关系,考查数形结合思想、分类讨论思想以及探求解决新问题的能力。
[解析](Ⅰ)解:因为椭圆过点(1,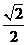 ),e=
),e=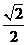 ,
所以
,
所以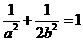 ,
,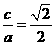 .
.
又a2=b2+c2,所以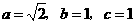 ,故所求椭圆方程为
,故所求椭圆方程为
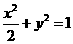 .
.
(Ⅱ)(i)设点P(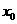 ,
,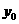 ),则
),则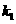 =
=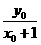 ,
,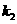 =
=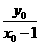 ,因为点
,因为点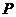 不在
不在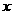 轴上,所以
轴上,所以
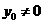 ,又
,又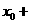
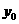 =2,所以
=2,所以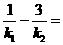
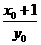
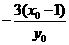 =
=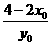
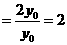 ,
,
因此结论成立。


11.(全国Ⅰ新卷文20)设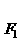 ,
, 分别是椭圆E:
分别是椭圆E: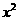 +
+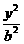 =1(0﹤b﹤1)的左、右焦点,过
=1(0﹤b﹤1)的左、右焦点,过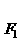 的直线
的直线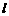 与E相交于A、B两点,且
与E相交于A、B两点,且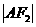 ,
,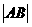 ,
,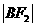 成等差数列。
成等差数列。
(Ⅰ)求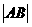
(Ⅱ)若直线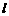 的斜率为1,求b的值。
的斜率为1,求b的值。
解: (1)由椭圆定义知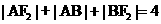
又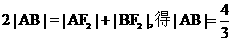
(2)L的方程式为y=x+c,其中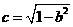
设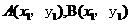 ,则A,B 两点坐标满足方程组
,则A,B 两点坐标满足方程组 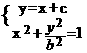
化简得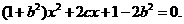 则
则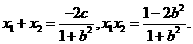
因为直线AB的斜率为1,所以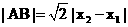 即
即 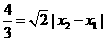 .
.
则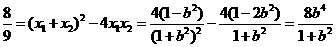 解得
解得 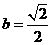 .
.
12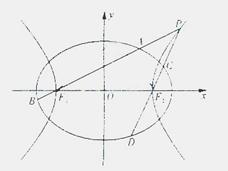 (山东卷理21)如图,已知椭圆
(山东卷理21)如图,已知椭圆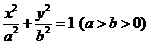 的离心率为
的离心率为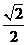 ,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长
,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长
为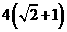 。一等轴双曲线的顶点是该椭圆的焦点,设
。一等轴双曲线的顶点是该椭圆的焦点,设
P为该双曲线上异于顶点的任一点,直线PF1和PF2与
椭圆的焦点分别为A、B和C、D。
(Ⅰ)求椭圆和双曲线的标准方程
(Ⅱ)设直线PF1、PF2的斜率分别为k1、k2,
证明:k1·k2=1
(Ⅲ)是否存在常数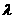 ,使得|AB|+|CD|=
,使得|AB|+|CD|=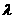 |AB|·|CD|
|AB|·|CD|
恒成立?若存在,求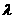 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
[解析](Ⅰ)由题意知,椭圆离心率为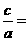
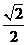 ,得
,得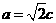 ,又
,又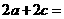
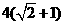 ,所以可解得
,所以可解得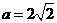 ,
,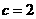 ,所以
,所以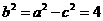 ,所以椭圆的标准方程为
,所以椭圆的标准方程为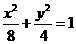 ;所以椭圆的焦点坐标为(
;所以椭圆的焦点坐标为(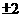 ,0),因为双曲线为等轴双曲线,且顶点是该椭圆的焦点,所以该双曲线的标准方程为
,0),因为双曲线为等轴双曲线,且顶点是该椭圆的焦点,所以该双曲线的标准方程为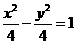 。
。
(Ⅱ)设点P(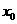 ,
,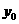 ),则
),则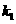 =
=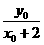 ,
,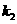 =
=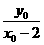 ,所以
,所以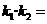
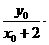
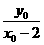 =
=
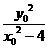 ,又点P(
,又点P(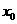 ,
,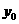 )在双曲线上,所以有
)在双曲线上,所以有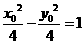 ,即
,即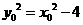 ,所以
,所以
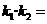
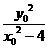 =1。
=1。
(Ⅲ)假设存在常数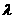 ,使得
,使得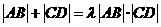 恒成立,则由(Ⅱ)知
恒成立,则由(Ⅱ)知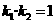 ,所以设直线AB的方程为
,所以设直线AB的方程为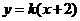 ,则直线CD的方程为
,则直线CD的方程为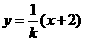 ,
,
由方程组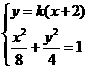 消y得:
消y得: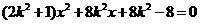 ,设
,设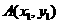 ,
,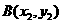 ,
,
则由韦达定理得: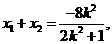
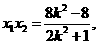
所以|AB|=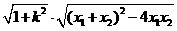 =
=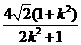 ,同理可得
,同理可得
|CD|=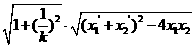 =
=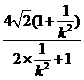 =
=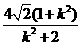 ,
,
又因为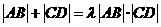 ,所以有
,所以有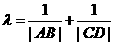 =
=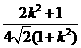 +
+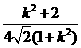
=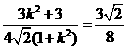 ,所以存在常数
,所以存在常数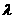
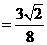 ,使得
,使得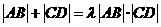 恒成立。
恒成立。
[命题意图]本题考查了椭圆的定义、离心率、椭圆与双曲线的标准方程、直线与圆锥曲线的位置关系,是一道综合性的试题,考查了学生综合运用知识解决问题的能力。其中问题(3)是一个开放性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力,
(标准答案)本小题主要考查椭圆、双曲线的基本概念和基本性质。考查直线和椭圆的位置关系,考查坐标化、定值和存在性问题,考查数行结合思想和探求问题的能力。
解(Ⅰ)设椭圆的半焦距为c,由题意知: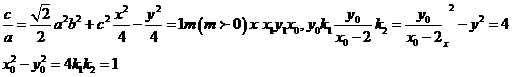
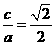 ,2a+2c=4(
,2a+2c=4(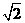 +1)所以a=2
+1)所以a=2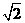 ,c=2,
,c=2,
又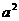 =
=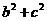 ,因此b=2。故 椭圆的标准方程为
,因此b=2。故 椭圆的标准方程为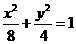
由题意设等轴双曲线的标准方程为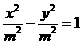
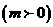 ,因为等轴双曲线的顶点是椭圆的焦点。所以m=2,
,因为等轴双曲线的顶点是椭圆的焦点。所以m=2,
因此 双曲线的标准方程为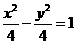
(Ⅱ)设A(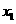 ,
,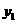 ),B(
),B(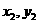 ),P(
),P(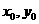 ),则
),则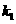 =
=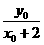 ,
,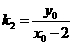 。
。
因为点P在双曲线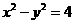 上,所以
上,所以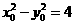 。
。
因此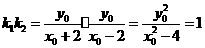 ,即
,即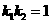

同理可得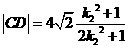 .
.
则 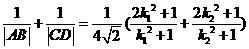 ,
,
又 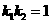 ,所以
,所以 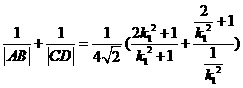
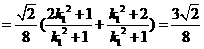 .
.
故 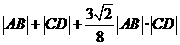
因此 存在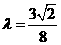 ,使
,使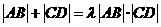 恒成立.
恒成立.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com