
题目列表(包括答案和解析)
7.(2010江西理数)4.
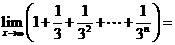 ( )
( )
A. 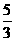 B.
B. 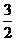 C. 2 D. 不存在
C. 2 D. 不存在
[答案]B

 w_w w. k#s5_
w_w w. k#s5_
[解析]考查等比数列求和与极限知识.解法一:先求和,然后对和取极限。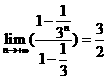
6.(2010江西理数)5.等比数列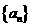 中,
中,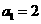 ,
,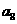 =4,函数
=4,函数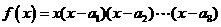 ,则
,则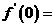 ( )
( )
A.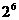 B.
B. 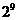 C.
C. 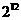 D.
D. 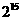
[答案]C

 w_w w. k#s5_
w_w w. k#s5_
[解析]考查多项式函数的导数公式,重点考查学生创新意识,综合与灵活地应用所学的数学知识、思想和方法。考虑到求导中,含有x项均取0,则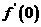 只与函数
只与函数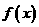 的一次项有关;得:
的一次项有关;得: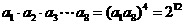 。
。
5.(2010全国卷2文数)(6)如果等差数列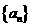 中,
中,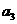 +
+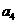 +
+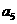 =12,那么
=12,那么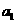 +
+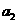 +•••…+
+•••…+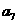 =
=
(A)14 (B) 21 (C) 28 (D) 35
[答案]C

 w_w w. k#s5_
w_w w. k#s5_
[解析]本题考查了数列的基础知识。
∵ 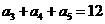 ,∴
,∴ 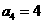
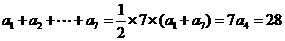
4.(2010辽宁理数)(6)设{an}是有正数组成的等比数列,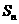 为其前n项和。已知a2a4=1,
为其前n项和。已知a2a4=1, 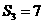 ,则
,则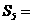


 w_w w. k#s5_
w_w w. k#s5_
(A)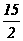 (B)
(B)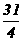 (C)
(C)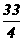 (D)
(D)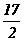
[答案]B
[命题立意]本题考查了等比数列的通项公式与前n项和公式,考查了同学们解决问题的能力。
[解析]由a2a4=1可得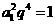 ,因此
,因此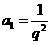 ,又因为
,又因为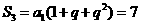 ,联力两式有
,联力两式有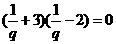 ,所以q=
,所以q= ,所以
,所以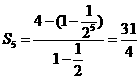 ,故选B。
,故选B。
3.(2010辽宁文数)(3)设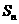 为等比数列
为等比数列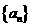 的前
的前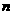 项和,已知
项和,已知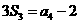 ,
,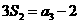 ,则公比
,则公比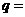


 w_w w. k#s5_
w_w w. k#s5_
(A)3 (B)4 (C)5 (D)6
答案B
解析:选B. 两式相减得,
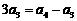 ,
,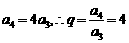 .
.
2.(2010全国卷2理数)(4).如果等差数列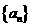 中,
中,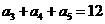 ,那么
,那么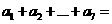
(A)14 (B)21 (C)28 (D)35
[答案]C
[命题意图]本试题主要考查等差数列的基本公式和性质.
[解析]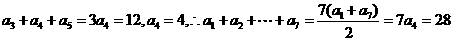
1.(2010浙江理数)(3)设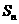 为等比数列
为等比数列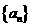 的前
的前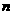 项和,
项和,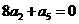 ,则
,则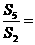
(A)11 (B)5 (C)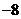 (D)
(D)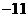
答案:D
解析:通过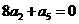 ,设公比为
,设公比为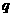 ,将该式转化为
,将该式转化为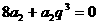 ,解得
,解得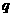 =-2,带入所求式可知答案选D,本题主要考察了本题主要考察了等比数列的通项公式与前n项和公式,属中档题
=-2,带入所求式可知答案选D,本题主要考察了本题主要考察了等比数列的通项公式与前n项和公式,属中档题
本资料来源于《》http://www.
|

|
版权所有:()
版权所有:()
(四)巩固练习:
1.已知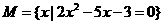 ,
,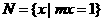 ,若
,若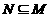 ,则适合条件的实数
,则适合条件的实数 的集合
的集合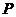 为
为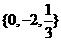 ;
;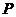 的子集有 8 个;
的子集有 8 个;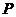 的非空真子集有 6 个.
的非空真子集有 6 个.
2.已知: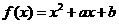 ,
,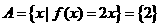 ,则实数
,则实数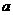 、
、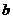 的值分别为
的值分别为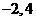 .
.
3.调查100名携带药品出国的旅游者,其中75人带有感冒药,80人带有胃药,那么既带感冒药又带胃药的人数的最大值为 75 ,最小值为 55 .
4.设数集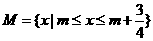 ,
,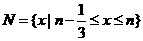 ,且
,且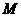 、
、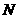 都是集合
都是集合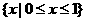 的子集,如果把
的子集,如果把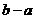 叫做集合
叫做集合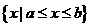 的“长度”,那么集合
的“长度”,那么集合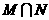 的长度的最小值是
的长度的最小值是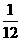 .
.
(三)例题分析:
例1.已知集合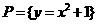 ,
,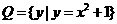 ,
,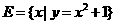 ,
,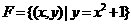 ,
,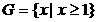 ,则
(
,则
( 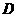 )
)
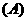
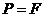
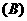
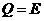

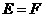
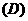
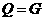
解法要点:弄清集合中的元素是什么,能化简的集合要化简.
例2.设集合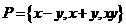 ,
,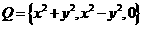 ,若
,若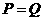 ,求
,求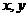 的值及集合
的值及集合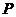 、
、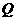 .
.
解:∵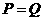 且
且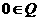 ,∴
,∴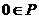 .
.
(1)若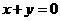 或
或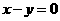 ,则
,则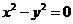 ,从而
,从而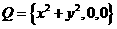 ,与集合中元素的互异性矛盾,∴
,与集合中元素的互异性矛盾,∴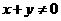 且
且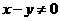 ;
;
(2)若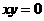 ,则
,则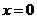 或
或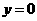 .
.
当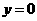 时,
时,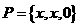 ,与集合中元素的互异性矛盾,∴
,与集合中元素的互异性矛盾,∴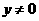 ;
;
当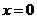 时,
时,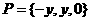 ,
,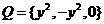 ,
,
由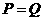 得
得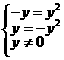 ①
或
①
或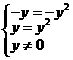 ②
②
由①得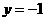 ,由②得
,由②得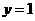 ,
,
∴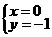 或
或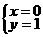 ,此时
,此时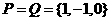 .
.
例3.设集合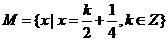 ,
, 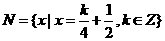 ,则(
,则( 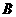 )
)
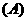
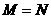
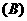
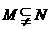

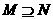
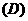
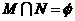
解法一:通分;
解法二:从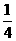 开始,在数轴上表示.
开始,在数轴上表示.
例4.若集合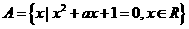 ,集合
,集合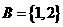 ,且
,且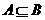 ,求实数
,求实数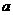 的取值范围.
的取值范围.
解:(1)若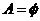 ,则
,则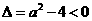 ,解得
,解得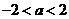 ;
;
(2)若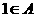 ,则
,则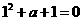 ,解得
,解得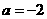 ,此时
,此时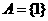 ,适合题意;
,适合题意;
(3)若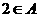 ,则
,则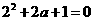 ,解得
,解得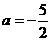 ,此时
,此时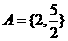 ,不合题意;
,不合题意;
综上所述,实数 的取值范围为
的取值范围为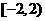 .
.
例5.设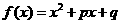 ,
,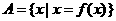 ,
,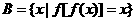 ,
,
(1)求证: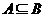 ;
;
(2)如果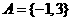 ,求
,求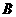 .
.
解答见《高考 计划(教师用书)》第5页.
计划(教师用书)》第5页.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com