
题目列表(包括答案和解析)
5.设函数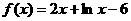 的零点为
的零点为 ,则
,则 的所在区间为( )
的所在区间为( )
(A) 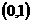 (B)
(B) 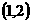 (C)
(C) 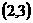 (D)
(D) 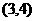
4.在区间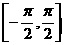 上随机取一个
上随机取一个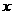 ,
,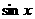 的值介于
的值介于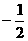 与
与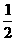 之间的概率为( )
之间的概率为( )
(A) 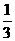 (B)
(B) 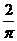 (C)
(C) 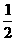 (D)
(D) 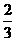
3.在等差数列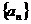 中,若
中,若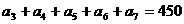 ,则
,则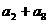 的值为( )
的值为( )
(A) 45 (B) 90 (C) 180 (D)300
2.在复平面内,复数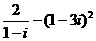 对应的点位于( )
对应的点位于( )
(A) 第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限
1.设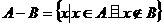 ,若
,若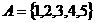 ,
,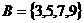 ,则
,则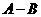 等于( )
等于( )
(A) 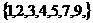 (B)
(B) 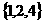 (C)
(C) 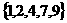 (D)
(D) 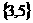
22.(文科 本题满分14分)
已知函数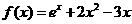 .
.
(Ⅰ)求证:函数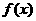 在区间
在区间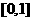 上存在唯一的极值点,并用二分法求函数取得极值时相应
上存在唯一的极值点,并用二分法求函数取得极值时相应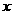 的近似值(误差不超过
的近似值(误差不超过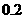 );(参考数据
);(参考数据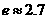 ,
,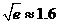 ,
,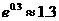 )
)
(Ⅱ)当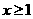 时,若关于
时,若关于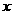 的不等式
的不等式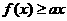 恒成立,试求实数
恒成立,试求实数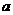 的取值范围.
的取值范围.
21.(本题满分12分)
已知椭圆 、抛物线
、抛物线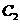 的焦点均在
的焦点均在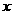 轴上,
轴上, 的中心和
的中心和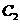 的顶点均为原点
的顶点均为原点 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
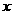 |
3 |
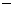 2 2 |
4 |
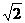 |
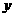 |
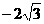 |
0 |
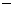 4 4 |
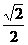 |
(Ⅰ)求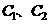 的标准方程;
的标准方程;
(Ⅱ)请问是否存在直线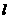 满足条件:①过
满足条件:①过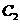 的焦点
的焦点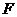 ;②与
;②与 交不同两点
交不同两点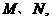 且满足
且满足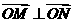 ?若存在,求出直线
?若存在,求出直线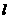 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
20.( 本题满分12分)
设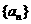 是公比大于
是公比大于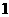 的等比数列,
的等比数列,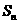 为数列
为数列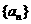 的前
的前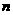 项和.已知
项和.已知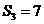 ,且
,且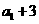 ,
,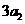 ,
,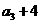 构成等差数列.
构成等差数列.
(Ⅰ)求数列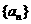 的通项公式;
的通项公式;
(Ⅱ)令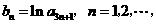 求数列
求数列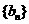 的前
的前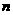 项和
项和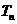 .
.
19.(本题满分12分)
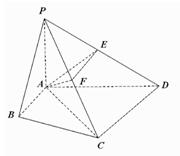 在四棱锥
在四棱锥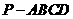 中,
中,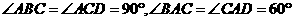 ,
,
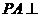 平面
平面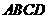 ,
,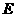 为
为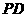 的中点,
的中点,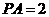 ,
,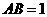 .
.
(Ⅰ) 求四棱锥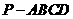 的体积
的体积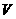 ;
;
(Ⅱ) 若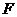 为
为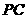 的中点,求证:
的中点,求证:
平面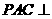 平面
平面 .
.
18.(本题满分12分)
有关部门要了解甲型H1N1流感预防知识在学校的普及情况,命制了一份有 道题的问卷到各学校做问卷调查.某中学
道题的问卷到各学校做问卷调查.某中学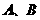 两个班各被随机抽取
两个班各被随机抽取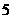 名学生接受问卷调查,
名学生接受问卷调查, 班
班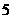 名学生得分为:
名学生得分为: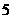 ,
,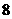 ,
,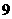 ,
,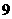 ,
,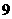 ;B班5名学生得分为:
;B班5名学生得分为: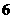 ,
,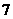 ,
,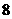 ,
,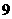 ,
, .
.
(Ⅰ)请你估计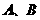 两个班中哪个班的问卷得分要稳定一些;
两个班中哪个班的问卷得分要稳定一些;
(Ⅱ)如果把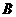 班
班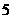 名学生的得分看成一个总体,并用简单随机抽样方法从中抽取样本容量为
名学生的得分看成一个总体,并用简单随机抽样方法从中抽取样本容量为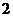 的
的 样本,求样本平均数与总体平均数之差的绝对值不小于
样本,求样本平均数与总体平均数之差的绝对值不小于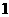 的概率.
的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com