
题目列表(包括答案和解析)
16. 设f(x)是R上的奇函数,且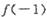 =0,当
=0,当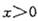 时,
时,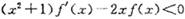 ,则不等式.
,则不等式.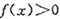 的解集为___________
的解集为___________
15. 设抛物线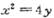 的焦点为F,经过点P(l,4)的直线l与抛物线相交于A、B两点,且点P恰为AB的中点,则
的焦点为F,经过点P(l,4)的直线l与抛物线相交于A、B两点,且点P恰为AB的中点,则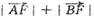 =___________
=___________
14.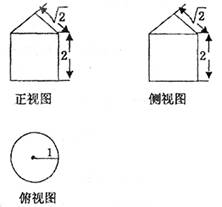 如图是一个几何体的三视图,则该几何体的表面积为________.
如图是一个几何体的三视图,则该几何体的表面积为________.
13. 若复数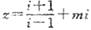 (i为虚数单位)为实数,则实数m=____________.
(i为虚数单位)为实数,则实数m=____________.
21.(本小题满分14分)
已知动圆过定点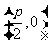 ,且与直线
,且与直线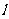 :
: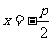 相切,其中
相切,其中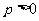 .
.
(Ⅰ)求动圆圆心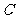 的轨迹方程;
的轨迹方程;
(Ⅱ)设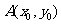 为轨迹C上一定点,经过A作直线AB、AC 分别交抛物线于B、C 两点,若 AB 和AC 的斜率之积为常数
为轨迹C上一定点,经过A作直线AB、AC 分别交抛物线于B、C 两点,若 AB 和AC 的斜率之积为常数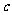 .求证:直线 BC 经过一定点,并
.求证:直线 BC 经过一定点,并
20. (本小题满分13分)
已知数列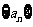 满足
满足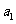 =1,且
=1,且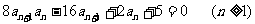
记 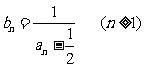
(Ⅰ)求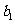 、
、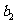 、
、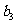 的值;
的值;
(Ⅱ) 求数列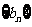 的通项公式及数列
的通项公式及数列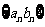 的前
的前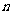 项和
项和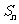 .
.
19.(本小题满分12分)
已知函数
(Ⅰ)求函数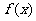 的单调区间;
的单调区间;
(Ⅱ)若集合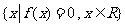 有且只有一个元素. 求正数
有且只有一个元素. 求正数 的取值范围.
的取值范围.
18. (本小题满分12分)
(本小题满分12分)
如图,三棱锥P-ABC中, PC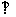 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD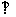 平面PAB.
平面PAB.
(I) 求证:AB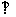 平面PCB;
平面PCB;
(II) 求异面直线AP与BC所成角的大小;
(Ⅲ)求二面角C-PA-B的正弦值
17.(本小题满分12分)
随机抽取某厂的某种产品400件,经质检,其中有一等品252件、二等品100件、三等品40件、次品8件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元.设1件产品的利润(单位:万元)为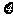 .
.
(Ⅰ)求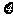 的分布列;
的分布列;
(Ⅱ)求1件产品的平均利润(即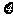 的数学期望);
的数学期望);
(III)经技术革新后,仍有四个等级的产品,但次品率降为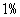 ,一等品率提高为
,一等品率提高为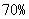 .如果此时要求1件产品的平均利润不小于4.75万元,则三等品率最多是多少?
.如果此时要求1件产品的平均利润不小于4.75万元,则三等品率最多是多少?
16. (本小题满分12分)
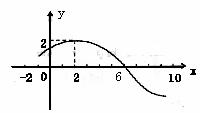 已知函数
已知函数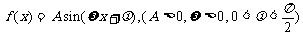 的图象如图所示.
的图象如图所示.
(Ⅰ)求函数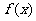 的解析式;
的解析式;
(Ⅱ)令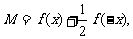 求
求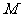 的最大值
的最大值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com